450. 刪除二叉搜索樹中的節點

文章目錄

• • • [450. 刪除二叉搜索樹中的節點](https://leetcode.cn/problems/delete-node-in-a-bst/)
    • • 一、題目
      • 二、題解
      • • 方法一：遞歸（一種麻煩的方法）
        • 方法二：優化后的遞歸

---

一、題目

給定一個二叉搜索樹的根節點 root 和一個值 key，刪除二叉搜索樹中的 key 對應的節點，并保證二叉搜索樹的性質不變。返回二叉搜索樹（有可能被更新）的根節點的引用。

一般來說，刪除節點可分為兩個步驟：

1. 首先找到需要刪除的節點；
2. 如果找到了，刪除它。

示例 1:

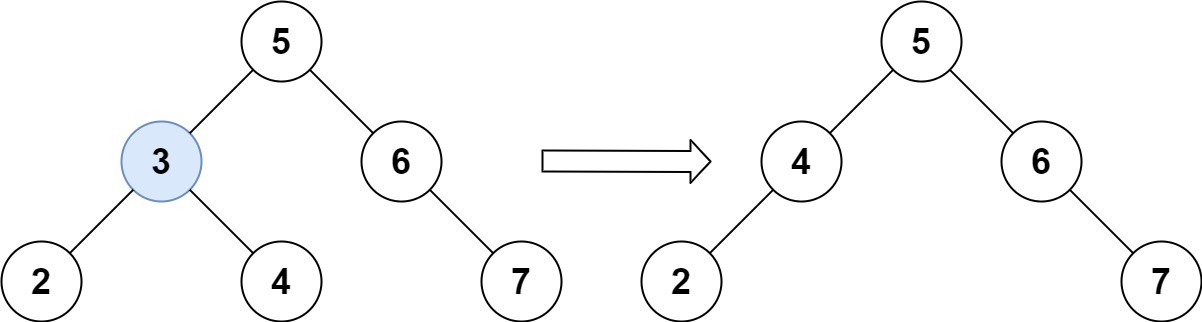
輸入：root = [5,3,6,2,4,null,7], key = 3
輸出：[5,4,6,2,null,null,7]
解釋：給定需要刪除的節點值是 3，所以我們首先找到 3 這個節點，然后刪除它。
一個正確的答案是 [5,4,6,2,null,null,7], 如下圖所示。
另一個正確答案是 [5,2,6,null,4,null,7]。

示例 2:

輸入: root = [5,3,6,2,4,null,7], key = 0
輸出: [5,3,6,2,4,null,7]
解釋: 二叉樹不包含值為 0 的節點

示例 3:

輸入: root = [], key = 0
輸出: []

提示:

• 節點數的范圍 [0, 104].
• -105 <= Node.val <= 105
• 節點值唯一
• root 是合法的二叉搜索樹
• -105 <= key <= 105

進階： 要求算法時間復雜度為 O(h)，h 為樹的高度。

二、題解

方法一：遞歸（一種麻煩的方法）

主要思路如下：

1. findNode 函數：這個函數用于在給定的二叉搜索樹中找到值等于 target 的節點。函數采用遞歸的方式，在樹中搜索目標節點。如果當前節點為空，說明未找到目標節點，返回 nullptr。如果當前節點的值等于目標值，返回該節點。如果當前節點的值大于目標值，說明目標節點在左子樹中，遞歸地搜索左子樹。否則，目標節點在右子樹中，遞歸地搜索右子樹。

2. deleteNode 函數：這個函數用于刪除二叉搜索樹中值為 key 的節點。首先，通過調用 findNode 函數找到待刪除的節點 node，同時維護一個指向 node 的父節點 pre。然后根據刪除情況進行不同的處理：

   • 如果 pre 為空，說明待刪除節點是根節點。然后根據左右子樹的情況進行調整，保留右子樹并將左子樹插入右子樹中的最左葉子節點。
   • 如果 pre 非空，根據 pre 的位置判斷 node 是其父節點的左子節點還是右子節點。然后根據左右子樹的情況進行調整，同樣保留右子樹并將左子樹插入右子樹中的最左葉子節點。

最后，刪除 node 節點并返回調整后的樹。

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:TreeNode *pre = nullptr;TreeNode* findNode(TreeNode *root, int target){if(root == nullptr){return root;}if(root->val == target){return root;}pre = root;if(root->val > target){TreeNode *left = findNode(root->left, target);return left;}else{TreeNode *right = findNode(root->right, target);return right;}}TreeNode* deleteNode(TreeNode* root, int key) {TreeNode *node = findNode(root, key);if(node == nullptr) return root;if(pre == nullptr){if(node->left && node->right){TreeNode *temp = node->right;while(temp->left){temp = temp->left;}temp->left = node->left;return node->right;}else if(node->left){return node->left;}else if(node->right){return node->right;}else{return nullptr;}}if(pre && pre -> right == node){if(node->left && node->right){TreeNode *temp = node->right;while(temp->left){temp = temp->left;}temp->left = node->left;pre->right = node->right;}else if(node->left){pre->right = node->left;}else if(node->right){pre->right = node->right;}else{pre->right = nullptr;}}if(pre && pre->left == node){if(node->left && node->right){TreeNode *temp = node->right;while(temp->left){temp = temp->left;}temp->left = node->left;pre->left = node->right;}else if(node->left){pre->left = node->left;}else if(node->right){pre->left = node->right;}else{pre->left = nullptr;}}delete node;return root;}
};

方法二：優化后的遞歸

算法思路

1. 遞歸搜索節點： 首先，我們從根節點開始遞歸地搜索目標節點（值為key的節點）。

   • 如果當前節點為空，表示沒有找到目標節點，直接返回空指針（nullptr）。
   • 如果當前節點的值大于目標key，說明目標節點在左子樹中，遞歸搜索左子樹。
   • 如果當前節點的值小于目標key，說明目標節點在右子樹中，遞歸搜索右子樹。
   • 如果當前節點的值等于目標key，說明找到了目標節點，繼續下一步。

2. 處理刪除操作： 一旦我們找到了目標節點，有幾種情況需要處理：

   • 如果目標節點沒有左子樹，那么我們可以用其右子樹來替代這個節點，然后刪除這個節點。
   • 如果目標節點沒有右子樹，類似地，我們可以用其左子樹來替代這個節點，然后刪除這個節點。
   • 如果目標節點既有左子樹又有右子樹，我們可以找到其右子樹中最小的節點（即右子樹中的最左節點，即后繼節點），將該節點的值復制到目標節點上，然后遞歸地在右子樹中刪除這個后繼節點。

3. 返回根節點： 最后，無論如何都要返回當前子樹的根節點。

具體實現

class Solution {
public:TreeNode* deleteNode(TreeNode* root, int key) {if (!root)return nullptr;if (root->val > key) {root->left = deleteNode(root->left, key); // 遞歸搜索左子樹} else if (root->val < key) {root->right = deleteNode(root->right, key); // 遞歸搜索右子樹} else {if (!root->left) { // 沒有左子樹，用右子樹替代TreeNode* temp = root->right;delete root;return temp;} else if (!root->right) { // 沒有右子樹，用左子樹替代TreeNode* temp = root->left;delete root;return temp;}TreeNode* temp = findMin(root->right); // 找到后繼節點root->val = temp->val;root->right = deleteNode(root->right, temp->val); // 在右子樹中刪除后繼節點}return root; // 返回根節點}private:TreeNode* findMin(TreeNode* node) {while (node->left)node = node->left;return node; // 找到最左節點，即后繼節點}
};

算法分析

• 在最壞情況下，我們需要遍歷BST的高度h，即時間復雜度為O(h)。
• 遞歸深度取決于樹的高度，所以空間復雜度也是O(h)。