直接看代碼：

import torch  
import numpy as np  
import random  
from IPython import display  
from matplotlib import pyplot as plt  
import torchvision  
import torchvision.transforms as transforms   mnist_train = torchvision.datasets.MNIST(root='/MNIST', train=True, download=True, transform=transforms.ToTensor())  
mnist_test = torchvision.datasets.MNIST(root='./MNIST', train=False,download=True, transform=transforms.ToTensor())  batch_size = 256 train_iter = torch.utils.data.DataLoader(mnist_train, batch_size=batch_size, shuffle=True,num_workers=0)  
test_iter = torch.utils.data.DataLoader(mnist_test, batch_size=batch_size, shuffle=False,num_workers=0)  num_inputs,num_hiddens,num_outputs =784, 256,10def init_param():W1 = torch.tensor(np.random.normal(0, 0.01, (num_hiddens,num_inputs)), dtype=torch.float32)  b1 = torch.zeros(1, dtype=torch.float32)  W2 = torch.tensor(np.random.normal(0, 0.01, (num_outputs,num_hiddens)), dtype=torch.float32)  b2 = torch.zeros(1, dtype=torch.float32)  params =[W1,b1,W2,b2]for param in params:param.requires_grad_(requires_grad=True)  return W1,b1,W2,b2def relu(x):x = torch.max(input=x,other=torch.tensor(0.0))  return xdef net(X):  X = X.view((-1,num_inputs))  H = relu(torch.matmul(X,W1.t())+b1)  #myrelu =((matmal x,w1)+b1),return  matmal(myrelu,w2 )+ b2return relu(torch.matmul(H,W2.t())+b2 )return torch.matmul(H,W2.t())+b2def SGD(paras,lr):  for param in params:  param.data -= lr * param.grad  def l2_penalty(w):return (w**2).sum()/2def train(net,train_iter,test_iter,loss,num_epochs,batch_size,lr=None,optimizer=None,mylambda=0):  train_ls, test_ls = [], []for epoch in range(num_epochs):ls, count = 0, 0for X,y in train_iter :X = X.reshape(-1,num_inputs)l=loss(net(X),y)+ mylambda*l2_penalty(W1) + mylambda*l2_penalty(W2)optimizer.zero_grad()l.backward()optimizer.step()ls += l.item()count += y.shape[0]train_ls.append(ls)ls, count = 0, 0for X,y in test_iter:X = X.reshape(-1,num_inputs)l=loss(net(X),y) + mylambda*l2_penalty(W1) + mylambda*l2_penalty(W2)ls += l.item()count += y.shape[0]test_ls.append(ls)if(epoch)%2==0:print('epoch: %d, train loss: %f, test loss: %f'%(epoch+1,train_ls[-1],test_ls[-1]))return train_ls,test_lslr = 0.01num_epochs = 20Lamda = [0,0.1,0.2,0.3,0.4,0.5]Train_ls, Test_ls = [], []for lamda in Lamda:print("current lambda is %f"%lamda)W1,b1,W2,b2 = init_param()loss = torch.nn.CrossEntropyLoss()optimizer = torch.optim.SGD([W1,b1,W2,b2],lr = 0.001)train_ls, test_ls = train(net,train_iter,test_iter,loss,num_epochs,batch_size,lr,optimizer,lamda)   Train_ls.append(train_ls)Test_ls.append(test_ls)x = np.linspace(0,len(Train_ls[1]),len(Train_ls[1]))plt.figure(figsize=(10,8))for i in range(0,len(Lamda)):plt.plot(x,Train_ls[i],label= f'L2_Regularization:{Lamda [i]}',linewidth=1.5)plt.xlabel('different epoch')plt.ylabel('loss')plt.legend(loc=2, bbox_to_anchor=(1.1,1.0),borderAxesPad = 0.)plt.title('train loss with L2_penalty')plt.show()

運行結果：

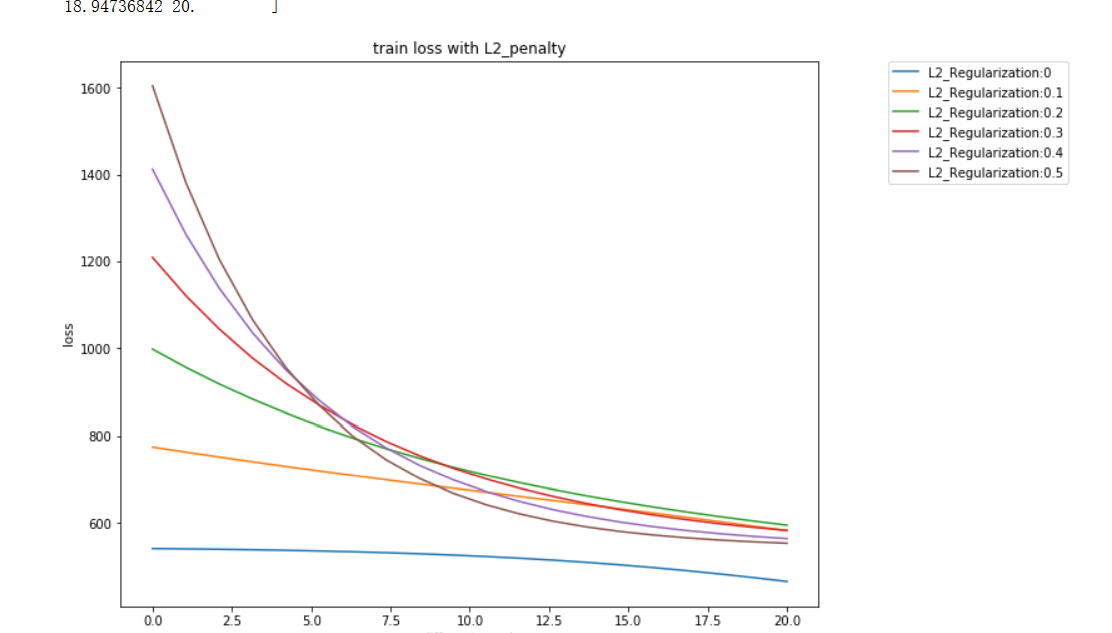
疑問和心得：

1. 畫圖的實現和細節還是有些模糊。
2. 正則化系數一般是一個可以根據算法有一定變動的常數。
3. 前饋神經網絡中，二分類最后使用logistic函數返回，多分類一般返回softmax值，若是一般的回歸任務，一般是直接relu返回。
4. 前饋神經網絡的實現，從物理層上應該是全連接的，但是網上的代碼一般都是兩層單個神經元，這個容易產生誤解。個人感覺，還是要使用nn封裝的函數比較正宗。