- (??? ),Hello我是祐言QAQ
- 我的博客主頁:C/C++語言,Linux基礎,ARM開發板,軟件配置等領域博主🌍
- 快上🚘,一起學習,讓我們成為一個強大的攻城獅!
- 送給自己和讀者的一句雞湯🤔:集中起來的意志可以擊穿頑石!
- 作者水平很有限,如果發現錯誤,可在評論區指正,感謝🙏
????????????????樹(Tree)是一種常用的數據結構,用于表示層次結構的數據關系。它由一組節點(Nodes)以及連接這些節點的邊(Edges)組成。樹的一個重要特征是一個節點可以有零個或多個子節點,但每個節點只有一個父節點(除了根節點),從而形成一種層次化的結構。

一、樹的基本概念
????????1.節點(Node):樹的基本構建單元。每個節點可以包含一個數據元素,以及指向其他節點的鏈接(邊)。樹中的每個節點除了根節點外,都有且只有一個父節點,但可以有零個或多個子節點。
????????2.根節點(Root):樹的頂層節點,它是整個樹的起始點,沒有父節點。
子節點(Children):一個節點的直接下層節點稱為它的子節點。一個節點可以有零個、一個或多個子節點。
????????3.父節點(Parent):一個節點的直接上層節點稱為它的父節點。
????????4.葉節點(Leaf):沒有子節點的節點稱為葉節點。葉節點位于樹的末端,它們沒有后繼節點。
????????5.高度(深度):樹的高度是指從根節點到樹中任意節點的最長路徑上的邊數。葉節點的高度為0,樹的高度取決于最深的路徑即樹中所有節點層次的最大值。
????????6.父子關系:樹中節點之間的連接形成了父子關系。每個節點都有一個唯一的父節點,除了根節點。
????????7.子樹(Subtree):對于一個節點,它的子樹是由該節點及其所有后代節點組成的一棵子樹。
????????8.節點的度(Degree):節點的度是指該節點擁有的子節點數量。二叉樹的度為2,二叉搜索樹的度可以是2或0/2。
????????9.樹的類型:樹有許多變種,包括二叉樹、二叉搜索樹、平衡樹、紅黑樹等。不同類型的樹在節點連接和數據存儲方面具有不同的特點和規則。

二、樹的特點
-
每棵樹僅包含一個根節點,作為樹的起始點。根節點是整個樹的頂層節點,沒有父節點與之關聯。
-
樹中的每個節點可以擁有多個孩子節點,但是不存在某個節點有多個父親節點。每個節點只有一個父節點,形成了清晰的父子關系。
-
樹中的葉子節點是沒有子節點的節點,葉子節點的度為 0。葉子節點位于樹的末端,沒有后繼節點,承載了終端數據。
-
樹中所有節點的度(子節點數量)之和加上1等于樹的總節點數。這一特點確保了每個節點的連接都被計算在內,形成了樹的整體結構。
三、二叉樹(Binary Tree)
????????一棵所有節點的度都不超過2的有序樹被稱為二叉樹。在二叉樹中,每個節點最多有兩個孩子,分別稱為左孩子和右孩子。即使節點只有一個孩子,仍然要區分左右孩子的位置。

1.完全二叉樹
????????完全二叉樹是指除最后一層外,其他所有層都是滿的,并且最后一層的節點從左到右依次排列。換句話說,最后一層可以不滿,但填充節點要從左至右進行。

2.滿二叉樹
????????滿二叉樹是一種特殊的完全二叉樹,它的每一層(包括最后一層)都被節點填滿,即每個節點的度都為2。

?3.二叉樹的特點
????????(1)如果一棵二叉樹的深度為 k,那么該二叉樹最多包含 2^k?1 個節點,最少包含 k 個節點。這是因為在深度為 k 的二叉樹中,每一層的節點數最多為 2^(k?1),而總節點數是各層節點數的累加,所以最多有 2^k?1 個節點,最少情況是當樹是一條鏈式結構時,只有一個路徑上的 k 個節點。
?????????(2)如果一棵完全二叉樹的深度為 k,那么該二叉樹最多包含 2^k?1 個節點,最少包含 2^(k?1)個節點。完全二叉樹的特點是除了最后一層外,其它層都是滿的,并且最后一層的節點依次從左至右排列。因此,完全二叉樹的節點數取決于最后一層的節點數。
學完上述這些內容就來試試這七個小練習吧,答案在評論區:
????????(1)一個深度為h的二叉樹最多有? ? ? ?個結點,最少有? ? ? ? 個結點。
????????(2)一棵具有 257個結點的完全二叉樹,它的深度為?? ? ? ?。
????????(3)不相交的樹的聚集稱之為? ? ? ?。
????????(4)深度為k的完全二叉樹至少有? ? ? ?個結點。至多有? ? ? ?個結點,
????????(5)高度為k,且有? ? ? ?個結點的二叉樹稱為滿二叉樹。
? ? ? ??(6)高度為6的完全二叉樹至少有? ? ? ?個結點。
四、二叉搜索樹(BST)
????????二叉搜索樹(Binary Search Tree,BST)是一種特殊的二叉樹,它具有以下特點和性質,使得在其中進行查找、插入和刪除等操作變得高效:
? ? ? ?1.節點結構:每個節點包含一個數據元素以及指向左子樹和右子樹的鏈接。
? ? ? ?2. 左子樹性質:對于樹中的每個節點,其左子樹中的所有節點的值都小于該節點的值。
? ? ? ?3. 右子樹性質:對于樹中的每個節點,其右子樹中的所有節點的值都大于該節點的值。
? ? ? ?4.遞歸定義:BST的定義是遞歸的,即每個子樹也是BST。

五、樹的遍歷
????????樹的遍歷是指按照一定的順序訪問樹中的所有節點,以便獲取節點的信息或執行某些操作。常用的樹的遍歷方式包括先序遍歷、中序遍歷、后序遍歷和按層遍歷。下面我們以上圖BST中的數據依次來演示并學習樹的遍歷。
1.先序遍歷:“根-左-右”
????????先序遍歷從根節點開始,首先訪問根節點,然后按照先左后右的順序遞歸遍歷左子樹和右子樹。先序遍歷的順序是從上到下,從左到右的方式。

????????遍歷結果:5 3 1 4 8 6 9。
2.中序遍歷:“左-根-右”
????????中序遍歷從根節點開始,先遞歸遍歷左子樹,然后訪問根節點,最后再遞歸遍歷右子樹。中序遍歷的順序是從左到右,節點值從小到大的方式。在二叉搜索樹中,中序遍歷能夠按升序輸出節點值。

?????????遍歷結果:1 3 4 5 6 8 9。
3.后序遍歷:“左-右-根”
????????后序遍歷從根節點開始,先遞歸遍歷左子樹,然后遞歸遍歷右子樹,最后訪問根節點。后序遍歷的順序是從下到上,從左到右的方式。

??????????遍歷結果:1 4 3 6 9 8 5。
4.按層遍歷
????????從根節點開始,逐層地從左到右訪問樹的節點。
????????按層遍歷使用隊列來實現,首先將根節點入隊,然后循環中,依次出隊當前層的節點,將它們的子節點入隊,以此類推,直到隊列為空。這樣能夠按照從上往下,從左往右的順序遍歷整個樹。

????????遍歷結果:5 3 8 1 4 6 9。
????????相信看完上邊的講解,你一定躍躍欲試想告訴我你已經學會了樹的遍歷,那么就讓題目來檢驗一下吧!(答案評論區見o)
????????(1)若某二叉樹的前序遍歷訪問順序是abdgcefh,中序遍歷訪問順序是dgbaechf,則其按層遍歷的結點訪問順序是?
????????(2)某二叉樹的中序遍歷結果為:ACBDFGEHI,先序遍歷結果:EDCABFGHI,后序遍歷結果是?
六、二叉搜索樹的實現
????????二叉樹的邏輯結構是非線性的,這意味著樹中的節點之間存在一對多的關系,即每個節點可以有多個子節點,但只有一個父節點(除了根節點沒有父節點)。
1.節點設計
typedef int Datatype;//二叉搜索樹節點結構體
typedef struct Node
{Datatype data;//數據域struct Node *lchild;左孩子的地址存放struct Node *rchild;//右孩子的地址存放
}BT_node, *B_tree;2.初始化
//初始化
B_tree init_tree(void)
{return NULL;//空的二叉搜索樹,就是初始化一個根節點為NULL的一個節點
}3.新建節點
//創建新節點
B_tree create_node(Datatype data)
{//為新節點申請空間B_tree new = malloc(sizeof(BT_node));if (new != NULL){//節點初始化new->data = data;new->lchild = NULL;new->rchild = NULL;}return new;
}4.插入節點
//插入節點:返回插入操作過后的根節點指針
//將new插入到以root為根節點的樹中,返回插入過后的樹的根節點
B_tree insert_node(B_tree root, B_tree new)
{if (new == NULL){return root;}//如果原來二叉搜索樹是空的,//那么第一次插入的節點就是根節點if(is_empty(root)){return new;}//原本有節點的情況else{//(1)新節點比root小,將new插入到root的左子樹中if (new->data < root->data){root->lchild = insert_node(root->lchild, new);}//(2)新節點比root大,將new插入到root的右子樹中else if (new->data > root->data){root->rchild = insert_node(root->rchild, new);}//(3)新節點與root相等,插入失敗else{printf("該節點存在,插入失敗\n");}}return root;
}5.查找節點
//查找節點
B_tree find_node(B_tree root, Datatype data)
{if (is_empty(root)){return NULL;}else{// (1)待查數據小于根節點數據,從左子樹中查找if (data < root->data){return find_node(root->lchild, data);}// (2)待查數據大于根節點數據,從右子樹中查找else if (data > root->data){return find_node(root->rchild, data);}// (3)待查數據等于根節點數據else{return root;}}
}6.刪除節點
//刪除節點
B_tree delete_node(B_tree root, Datatype data)
{if (is_empty(root)){return root;}else{//待刪數據比根節點數據小,在根節點的左子樹中刪除if (data < root->data){root->lchild = delete_node(root->lchild, data);}//待刪數據比根節點數據大,在根節點的右子樹中刪除else if (data > root->data){root->rchild = delete_node(root->rchild, data);}//待刪數據與根節點數據相等,那么根節點就是待刪節點else{//當待刪節點有左子樹,用左子樹中最大節點接替待刪節點if (root->lchild != NULL){//找左子樹最大節點:不斷往右邊找B_tree tmp = NULL;for (tmp=root->lchild; tmp->rchild!=NULL; tmp=tmp->rchild);root->data = tmp->data;//接替//然后在左子樹中刪掉用來接替的節點root->lchild = delete_node(root->lchild, tmp->data);}//當待刪節點只有右子樹,用右子樹中最小節點接替待刪節點else if (root->rchild != NULL){//找右子樹最小節點:不斷往左邊找B_tree tmp = NULL;for (tmp=root->rchild; tmp->lchild!=NULL; tmp=tmp->lchild);root->data = tmp->data;//然后在右子樹中刪掉用來接替的節點root->rchild = delete_node(root->rchild, tmp->data);}//當待刪節點是目前子樹的根節點,直接刪除else{free(root);root = NULL;}}}return root;
}7.遍歷
//(1)先序遍歷 根節點-左子樹-右子樹
void pre_travel(B_tree root)
{if (is_empty(root)){return;}printf("%d ", root->data);pre_travel(root->lchild);pre_travel(root->rchild);
}
//(2)中序遍歷 左子樹-根節點-右子樹
void mid_travel(B_tree root)
{if (is_empty(root)){return;}mid_travel(root->lchild);printf("%d ", root->data);mid_travel(root->rchild);
}//(3)后序遍歷 左子樹-右子樹-根節點
void post_travel(B_tree root)
{if (is_empty(root)){return;}post_travel(root->lchild);post_travel(root->rchild);printf("%d ", root->data);
}//(4)按層遍歷
void level_travel(B_tree root)
{if (root == NULL){return;}//創建一個空隊列Lq q = init_queue();//將根節點數據入隊in_queue(q, creat_queue_node(root->data));Link get_queue_node;//獲取出隊元素的地址while(1){//出隊隊首(如果隊列為空,遍歷結束,跳出循環)if (!out_queue(q, &get_queue_node)){break;}//出隊的時候打印這個元素printf("%d ", get_queue_node->data);//出隊數據對應的樹節點的左右孩子入隊B_tree tree_node = find_node(root, get_queue_node->data);if (tree_node->lchild != NULL){in_queue(q, creat_queue_node(tree_node->lchild->data));}if(tree_node->rchild != NULL){in_queue(q, creat_queue_node(tree_node->rchild->data));}}
}
七、自平衡樹 AVL
????????AVL樹(Adelson-Velsky and Landis tree)是一種自平衡二叉搜索樹,它在插入和刪除操作后會自動調整節點的位置,以保持樹的平衡性。平衡性指的是樹的左右子樹高度差不超過1,從而保證樹的查找、插入和刪除操作的時間復雜度都能保持在較低的水平。
????????此外AVL樹的平衡性是通過節點的高度差(稱為平衡因子)來維護的。平衡因子是左子樹高度減去右子樹高度的值。在AVL樹中,每個節點的平衡因子必須在-1、0和1之間。

1.左-左(LL)不平衡
????????當一個節點的左子樹的左子樹高度比右子樹高度大2或更多時,就會發生LL不平衡。這可以通過右旋操作來解決。

2.左-右(LR)不平衡
????????當一個節點的左子樹的右子樹高度比左子樹高度大2或更多時,就會發生LR不平衡。這可以通過先對左子樹進行左旋,然后對整個樹進行右旋來解決。

3.右-右(RR)不平衡
????????當一個節點的右子樹的右子樹高度比左子樹高度大2或更多時,就會發生RR不平衡。這可以通過左旋操作來解決。

4.右-左(RL)不平衡
???????? 當一個節點的右子樹的左子樹高度比右子樹高度大2或更多時,就會發生RL不平衡。這可以通過先對右子樹進行右旋,然后對整個樹進行左旋來解決。

八、AVL代碼實現
1.數據結構定義
?????????定義一個結構 Avl_node 來表示AVL樹的節點,包括節點的數據、高度、左孩子和右孩子。
typedef int Datatype;typedef struct Avl_Node
{Datatype data; //數據int height; //高度struct Avl_Node *lchild; //左孩子struct Avl_Node *rchild; //右孩子
}Avl_node;2.初始化和創建節點
????????通過 init_avl 函數初始化一棵空的AVL樹,?create_avl_node 函數創建一個新的AVL節點。
//初始化
Avl_node *init_avl()
{return NULL;
}//創建節點
Avl_node *create_avl_node(Datatype data)
{Avl_node *new = malloc(sizeof(Avl_node));if (new != NULL){new->data = data;new->height = 1;new->lchild = NULL;new->rchild = NULL;}return new;
}3.獲取孩子的高度并更新
?????????? get_height 函數用于獲取節點的高度,max 函數用于更新兩個整數中的較大值。
//獲取孩子的高度
int get_height(Avl_node *root)
{if (root == NULL){return 0;}return root->height;
}//高度更新
int max(int h1, int h2)
{return h1>h2?h1:h2;
}4.左旋和右旋操作
?????????avl_left 函數實現左旋操作,avl_right 函數實現右旋操作,通過這些操作可以調整樹的結構以維持平衡。
//左旋
Avl_node *avl_left(Avl_node *root)
{Avl_node *tmp = root->rchild;root->rchild = tmp->lchild;tmp->lchild = root;root->height = max(get_height(root->lchild), get_height(root->rchild))+1;tmp->height = max(get_height(tmp->lchild), get_height(tmp->rchild))+1;return tmp;
}//右旋
Avl_node *avl_right(Avl_node *root)
{Avl_node *tmp = root->lchild;root->lchild = tmp->rchild;tmp->rchild = root;root->height = max(get_height(root->lchild), get_height(root->rchild))+1;tmp->height = max(get_height(tmp->lchild), get_height(tmp->rchild))+1;return tmp;
}5.自平衡處理
??avl_opt 函數用于在插入和刪除節點后進行自平衡處理,根據節點的高度差進行旋轉操作來維持樹的平衡性。
//自平衡處理
Avl_node *avl_opt(Avl_node *root)
{//(1)左邊不平衡//root的左子樹高度-右子樹高度 > 1if (get_height(root->lchild)-get_height(root->rchild)>1){// ①左-左不平衡:(root->lchild->lchild)的高度 >= (root->lchild->rchild)的高度if (get_height(root->lchild->lchild) >= get_height(root->lchild->rchild)){//右旋root = avl_right(root);}// ②左-右不平衡:(root->lchild->lchild)的高度 < (root->lchild->rchild)的高度else if (get_height(root->lchild->lchild) < get_height(root->lchild->rchild)){//左旋root->lchild = avl_left(root->lchild);//右旋root = avl_right(root);}}//(2)右邊不平衡 root的右子樹高度-左子樹高度 > 1else if (get_height(root->rchild)-get_height(root->lchild)>1){// ③右-右不平衡:(root->rchild->rchild)的高度 >= (root->rchild->lchild)的高度if (get_height(root->rchild->rchild) >= get_height(root->rchild->lchild)){//左旋root = avl_left(root); }// ④右-左不平衡:(root->rchild->rchild)的高度 < (root->rchild->lchild)的高度else if (get_height(root->rchild->rchild) < get_height(root->rchild->lchild)){//右旋root->rchild = avl_right(root->rchild);//左旋root = avl_left(root);} }//(3)平衡else{}return root;
}6.插入節點
???????? insert_avl_node 函數用于將新節點插入AVL樹中,并在插入后執行自平衡操作。
//插入節點
Avl_node *insert_avl_node(Avl_node *root, Avl_node *new)
{if (new == NULL){return root;}//如果是第一次插入,沒有任何節點if (root == NULL){return new;}else{//新節點放在根的左邊,還是右邊if (new->data < root->data)//新節點小于根節點,放左邊{//根節點的左邊還有左孩子的情況 root->lchild = insert_avl_node(root->lchild, new);}else if (new->data > root->data)//新節點大于根節點,放右邊{//根節點的右邊還有右孩子的情況root->rchild = insert_avl_node(root->rchild, new);}else{printf("二叉樹里面已經有這個節點\n");}}//自平衡處理root = avl_opt(root);//高度更新root->height = max(get_height(root->lchild), get_height(root->rchild))+1;return root;
}7.遍歷操作
? ?display_prec 和 display_mid 函數分別實現了AVL樹的先序遍歷和中序遍歷。
//先序
void display_prec(Avl_node *root)
{if (root == NULL){return ;}printf("%d ", root->data);display_prec(root->lchild);display_prec(root->rchild);
}//中序
void display_mid(Avl_node *root)
{if (root == NULL){return ;}display_mid(root->lchild);printf("%d ", root->data);display_mid(root->rchild);
}8.刪除節點
? ?dele_node 函數用于刪除指定數據的節點,并根據情況進行自平衡操作。
//刪除節點
Avl_node *dele_node(Avl_node *root, Datatype data)
{if (root == NULL){return root;}else{//如果刪除節點比根節點小,去左子樹中找要刪除的節點if (root->data > data){root->lchild = dele_node(root->lchild, data);}//如果刪除節點比根節點大,去右子樹中找要刪除的節點else if (root->data < data){root->rchild = dele_node(root->rchild, data);}//刪除節點等于根節點else{//1、當待刪除的節點有左子樹,用左子樹中最大的值來替換掉刪除的節點//保證二叉樹滿足BST的特性if (root->lchild!=NULL){//找左子樹中最大的節點,不斷往右找Avl_node *tmp = NULL;for (tmp = root->lchild; tmp->rchild!=NULL; tmp = tmp->rchild);//最大的節點接替要刪除的節點root->data = tmp->data;//然后在左子樹中刪掉用來接替的節點root->lchild = dele_node(root->lchild, tmp->data);}//2、當待刪除的節點沒有左子樹,只有右子樹,用右子樹中最小的值來替換掉刪除的節點else if (root->rchild!=NULL){//找右子樹中最小的節點,不斷往左找Avl_node *tmp = NULL;for(tmp=root->rchild; tmp->lchild!=NULL; tmp = tmp->lchild);//最小的節點接替要刪除的節點root->data = tmp->data; //然后在右子樹中刪掉用來接替的節點root->rchild = dele_node(root->rchild, tmp->data);}//3、待刪除節點,即沒有左子樹,也沒有右子樹,就是一個葉子節點,直接刪除else{free(root);root = NULL;}}}//如果刪除的節點返回的root為空if (root == NULL){return root;}//自平衡處理root = avl_opt(root);//高度更新root->height = max(get_height(root->lchild), get_height(root->rchild))+1;return root;
}9.例程
? ? ? ??循環讀取輸入的正整數和負整數,正整數表示插入節點,負整數表示刪除節點,0 表示輸出遍歷結果:

int main(int argc, char const *argv[])
{//初始化一棵空的avl樹Avl_node *root = init_avl();//新建節點并插入樹結構int num;while(1){ scanf("%d", &num);if (num > 0){//新建節點Avl_node * new = create_avl_node(num);//插入節點root = insert_avl_node(root, new);}else if (num < 0){root = dele_node(root, -num);}else{printf("先序遍歷:");display_prec(root);printf("\n中序遍歷:");display_mid(root);printf("\n");}}return 0;
}九、哈夫曼樹
????????哈夫曼樹(Huffman Tree)是一種用于編碼和壓縮數據的樹形數據結構。它是一種特殊的二叉樹,用于將出現頻率較高的字符(或符號)用較短的二進制編碼表示,從而實現數據的高效存儲和傳輸。
? ? ? ? 也可以說當有n個葉子節點,每個節點都有各自的權,試圖創建一個帶權路徑長度最小的樹,這棵樹就是最優二叉樹就叫哈夫曼樹。
1.基本概念
????????在下面的例子中,我們將解釋路徑、路徑長度、結點的權、結點的帶權路徑長度以及樹的帶權路徑長度(WPL)。

? ? ? ? (1)路徑: 路徑是從一個節點到另一個節點的通路。例如,從根節點到節點 5 的路徑可以是:15 -> 8 -> 5。
????????(2)路徑長度: 在一條路徑中,每經過一個節點,路徑長度都要加 1。例如,從根節點到節點 5 的路徑長度為 2(15 -> 8 -> 5)。
? ? ? ? (3)結點的權: 每個節點都有一個權重值。在這個例子中,節點 15 的權重為 15,節點 8 的權重為 8,以此類推。
? ? ? ? (4)結點的帶權路徑長度: 結點的帶權路徑長度是指從根節點到該節點之間的路徑長度與該節點的權重的乘積。例如,節點 5 的帶權路徑長度為 2(路徑長度) * 5(權重) = 10。
????????(5)樹的帶權路徑長度(WPL): 樹的帶權路徑長度是指樹中所有葉子節點的帶權路徑長度之和。在這個例子中,樹的 WPL 為:(2 * 3) + (2 * 5) + (3 * 7) + (3 * 8) + (3 * 12) + (1 * 15) = 84。
2.哈夫曼編碼
????????哈夫曼編碼是一種用于將字符或符號編碼為二進制的壓縮編碼方法,旨在通過分配較短的編碼給出現頻率較高的字符,以實現數據的高效壓縮和傳輸。這種編碼方式以哈夫曼樹為基礎,根據字符出現的頻率構建一個最優的二叉樹,然后通過從根節點到葉子節點的路徑來表示字符的編碼。
????????下面是哈夫曼編碼的基本步驟:
(1)統計字符頻率: 對要編碼的數據進行字符頻率的統計,通常使用頻率表來記錄每個字符出現的次數。
(2)構建哈夫曼樹: 根據字符頻率構建哈夫曼樹,即從頻率最低的葉子節點開始,每次選擇兩個頻率最低的節點作為子節點,將它們的頻率相加作為父節點的頻率,重復這個過程直到只剩下一個根節點。
(3)分配編碼: 在哈夫曼樹中,沿著左子樹路徑走的編碼為 0,沿著右子樹路徑走的編碼為 1。從根節點開始,沿著路徑到達葉子節點,記錄路徑上的編碼,即可得到字符的哈夫曼編碼。
(4)生成編碼表: 將字符和對應的哈夫曼編碼建立映射關系,構建編碼表,以便后續編碼和解碼使用。
????????下面就讓我們動手來畫一個哈夫曼樹并構建編碼表:

?????????這是我們統計的字符頻率,下面就從頻率最小的兩個字符開始,從下往上繪制二叉樹,每繪制一個二叉樹就要把其和求出來給到根,再從剩余的多有字符和根中調出次小的兩個值,再次形成一個二叉樹,以此類推直到完成所有。然后再對其分配編碼,沿著左子樹路徑走的編碼為 0,沿著右子樹路徑走的編碼為 1。

? ? 3.哈弗曼樹的應用領域??
????????哈夫曼樹的主要思想是將頻率較高的字符分配較短的編碼,而頻率較低的字符分配較長的編碼,以便在編碼和解碼過程中減少數據的長度。這種編碼方式稱為哈夫曼編碼,它是一種前綴編碼,即任何一個字符的編碼不是另一個字符編碼的前綴,從而確保解碼時不會產生歧義。
? ? ? ? 因此哈夫曼樹在信息傳輸、數據存儲和壓縮領域具有重要的應用,常用于壓縮文件、圖像、音頻等數據,以便有效地減少存儲空間和傳輸帶寬。由于哈夫曼編碼是無損壓縮,解碼后可以完全還原原始數據,因此被廣泛應用于通信和存儲領域。
????????為了方便大家理解與掌握,那么再出一道題(答案評論區)。

4. 數組方式構建哈夫曼樹(C語言)? ??
#include <stdio.h>
#include <stdlib.h>#define MAX_TREE_HT 100 // 定義最大樹高struct MinHeapNode { // 定義最小堆節點的結構體char data; // 節點數據unsigned freq; // 節點頻率struct MinHeapNode *left, *right; // 左右子節點指針
};struct MinHeap { // 定義最小堆結構體,用于構建哈夫曼樹unsigned size; // 堆的大小unsigned capacity; // 堆的容量struct MinHeapNode** array; // 存儲堆節點指針的數組
};struct MinHeapNode* newNode(char data, unsigned freq) { // 創建新的最小堆節點struct MinHeapNode* temp = (struct MinHeapNode*)malloc(sizeof(struct MinHeapNode)); // 分配節點內存temp->left = temp->right = NULL; // 初始化左右子節點指針為空temp->data = data; // 設置節點數據temp->freq = freq; // 設置節點頻率return temp; // 返回新創建的節點
}struct MinHeap* createMinHeap(unsigned capacity) { // 創建最小堆struct MinHeap* minHeap = (struct MinHeap*)malloc(sizeof(struct MinHeap)); // 分配堆內存minHeap->size = 0; // 初始化堆大小為0minHeap->capacity = capacity; // 設置堆容量minHeap->array = (struct MinHeapNode**)malloc(minHeap->capacity * sizeof(struct MinHeapNode*)); // 分配存儲節點指針的數組內存return minHeap; // 返回新創建的堆
}void swapMinHeapNode(struct MinHeapNode** a, struct MinHeapNode** b) { // 交換最小堆節點struct MinHeapNode* t = *a; // 臨時變量保存節點a的值*a = *b; // 將節點b的值賦給節點a*b = t; // 將臨時變量中保存的節點a的值賦給節點b
}void minHeapify(struct MinHeap* minHeap, int idx) { // 對最小堆進行維護,確保滿足最小堆性質int smallest = idx; // 初始化最小元素索引為傳入的索引int left = 2 * idx + 1; // 左子節點索引int right = 2 * idx + 2; // 右子節點索引if (left < minHeap->size && minHeap->array[left]->freq < minHeap->array[smallest]->freq)smallest = left; // 如果左子節點的頻率小于最小元素的頻率,則更新最小元素索引if (right < minHeap->size && minHeap->array[right]->freq < minHeap->array[smallest]->freq)smallest = right; // 如果右子節點的頻率小于最小元素的頻率,則更新最小元素索引if (smallest != idx) { // 如果最小元素索引不等于傳入的索引swapMinHeapNode(&minHeap->array[smallest], &minHeap->array[idx]); // 交換最小元素和傳入索引對應的元素minHeapify(minHeap, smallest); // 遞歸調整子堆}
}int isSizeOne(struct MinHeap* minHeap) { // 判斷堆的大小是否為1return (minHeap->size == 1); // 如果堆的大小為1,則返回1,否則返回0
}struct MinHeapNode* extractMin(struct MinHeap* minHeap) { // 從堆中取出頻率最小的節點struct MinHeapNode* temp = minHeap->array[0]; // 獲取堆的根節點minHeap->array[0] = minHeap->array[minHeap->size - 1]; // 將堆的最后一個節點移動到根節點--minHeap->size; // 減小堆的大小minHeapify(minHeap, 0); // 調整堆,確保滿足最小堆性質return temp; // 返回取出的節點
}void insertMinHeap(struct MinHeap* minHeap, struct MinHeapNode* minHeapNode) { // 向堆中插入節點++minHeap->size; // 增加堆的大小int i = minHeap->size - 1; // 獲取插入節點的索引while (i && minHeapNode->freq < minHeap->array[(i - 1) / 2]->freq) { // 如果插入節點的頻率小于其父節點的頻率minHeap->array[i] = minHeap->array[(i - 1) / 2]; // 將父節點向下移動i = (i - 1) / 2; // 更新索引為父節點的索引}minHeap->array[i] = minHeapNode; // 將插入節點放入合適的位置
}void buildMinHeap(struct MinHeap* minHeap) { // 構建最小堆int n = minHeap->size - 1; // 獲取堆的大小int i;for (i = (n - 1) / 2; i >= 0; --i) // 從堆的非葉子節點開始,逐步調整堆以滿足最小堆性質minHeapify(minHeap, i);
}struct MinHeap* createAndBuildMinHeap(char data[], int freq[], int size) { // 創建并構建最小堆struct MinHeap* minHeap = createMinHeap(size); // 創建最小堆for (int i = 0; i < size; ++i)minHeap->array[i] = newNode(data[i], freq[i]); // 將數據和頻率轉化為最小堆節點插入堆中minHeap->size = size; // 設置堆的大小為傳入的大小buildMinHeap(minHeap); // 構建最小堆return minHeap; // 返回構建好的最小堆
}
十、紅黑樹
1.基本概念和特點
????????紅黑樹(Red-Black Tree)是一種自平衡二叉搜索樹,?紅黑樹滿足平衡的要求為:左右子樹高度差不能超過一倍;一般稱其為相對平衡樹,而叫AVl為絕對平衡樹。它具有以下特點:
????????(1)樹中的節點都是有顏色的,要么紅色要么黑色;
????????(2)樹的根節點顏色是黑色;
????????(3)空節點的顏色算作黑色;
????????(4)不能有連續的紅色節點(任意一對父子節點不可能都是紅色節點),但黑色節點可任意連續;
????????(5)從任意一個節點開始到葉子節點的路徑包含的黑色節點個數是相等的。
2.紅黑樹節點的插入
????????(1)創建新節點,著色為紅色;
? ? ? ? (2)如果樹為空,將該節點顏色設置為黑色,作為樹的根節點;
? ? ? ? (3)如果樹不為空,用BST的方式插入新節點;
? ? ? ? (4)判斷樹是否平衡,做平衡處理。
3.紅黑樹不平衡處理

? ? ? ? ?一個基本的紅黑樹包含,根節點G(祖父)、P節點(父)、U節點(叔)以及新節點(N),下面我們就N的不同來討論當紅黑樹不平衡是該如何使之平衡。
????????(1)當父節點P的顏色為黑色,直接插入不影響平衡性
????????(2)當父節點P的顏色為紅色時我們就要分多組來討論了,首先是:
①叔叔節點U的顏色也是紅色
? ? ? ?I.父親節點為祖父節點的左孩子
???????????????·新節點是左孩子
? ? ? ? ? ? ????????????????a.直接將U和P顏色改為黑色,G的顏色該為紅色
??????????????????????????? b.將祖父節點作為新節點取討論平衡性

?????????????·新節點是右孩子
? ? ? ? ? ? ????????????????a.直接將U和P顏色改為黑色,G的顏色改為紅色
??????????????????????????? b.將祖父節點作為新節點取討論平衡性

? ? ? ?II.父親節點為祖父節點的右孩子
? ? ? ? ? ? 這種情況與上述的父親節點為祖父節點的左孩子基本一致,只是更換了方向,結和上兩幅圖很容易推理得出,這里就不贅述了。
②叔叔節點U的顏色為黑色
? ? ? ? I.父親節點為祖父節點的左孩子
????????????????·新節點是左孩子
? ? ? ? ? ? ? ? ? ? ? ? a.將P和G變顏色
? ? ? ? ? ? ? ? ? ? ? ? b.將現在的P和G進行右旋

??????????????????·新節點是右孩子
??????????????????????????? ? a.將P和N這組關系進行左旋
??????????????????????????????b.將變化過后的新的P和G變顏色
??????????????????????????????c.將現在的P和G進行右旋

????????II.父親節點為祖父節點的右孩子
??????????????????·新節點是左孩子
??????????????????????????????a.將P和N進行右旋
??????????????????????????????b.將變化后的P和G變顏色
??????????????????????????????c.將現在的P和G進行左旋

????????????????·新節點是右孩子
????????????????????????????????a.將變化后的P和G變顏色
????????????????????????????????b.將現在的P和G進行左旋
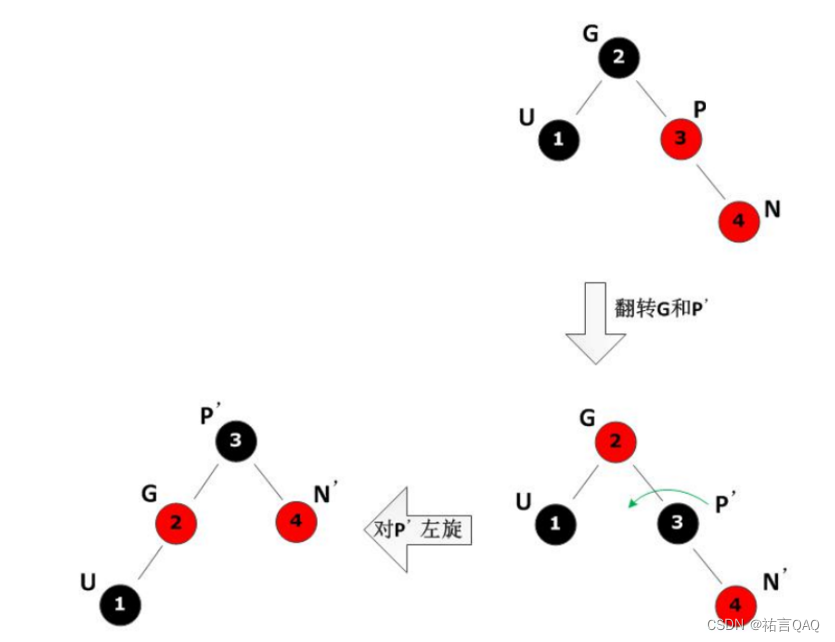
?????????對于紅黑樹呢代碼也較為復雜,因此我們只需掌握基本邏輯即可,代碼可在網上很容易搜到,有興趣的同學自己找一下,也可以來找我私信。
????????更多C語言、Linux系統、ARM板實戰和數據結構相關文章,關注專欄:
? ?手撕C語言
? ? ? ? ? ? 玩轉linux
????????????????????腳踢數據結構
?? ? ? ? ? ? ? ? ?? ? ? ? ? 6818(ARM)開發板實戰
📢寫在最后
- 今天的分享就到這啦~
- 覺得博主寫的還不錯的煩勞?
一鍵三連喔~ - 🎉感謝關注🎉


:背后的工作原理解析“)








終)







