給定信號,
令小波變換的尺度
則x(t)的二進小波變換為
令為
取模極大值時的橫坐標,那么
就是模極大值。
目標是由坐標、模極大值
及最后一級的低頻分量
重建信號x(t)
為了重建x(t),假定有一信號集合h(t),該集合中信號的小波變換和x(t)的小波變換具有相同的模極大值。希望在某一準則下在h(t)中選取一個信號來最佳地近似x(t)。
記h(t)的小波變換為,則對
的制約條件有:
(1)對應每一個尺度j,在所有的模極大值橫坐標處,都應有
(2)對應每一個尺度j,的局部極值都應位于模極大值橫坐標
處
對于條件(1),設U是希爾伯特空間中的一個子空間,并假定U是由一組函數
所張成的。那么,h(t)在U上的正交投影應該等于x(t)在U上的正交投影。
令O是U的正交補空間,則,
對于條件(2),

交替投影法
V:上所有信號的二進小波變換所組成的空間
K:序列所組成的空間,
滿足:
?
:空間K上的一個閉包,
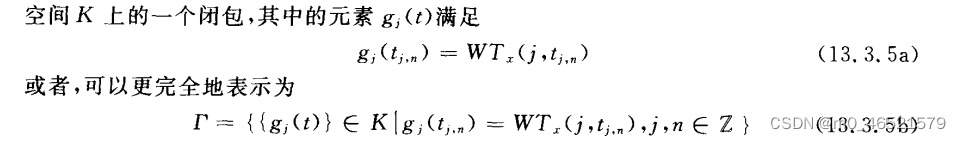 ?
?
?


)








方法:監聽保存進度,進度條等方法)
))





詳解)
