聲明

該系列文章僅僅展示個人的解題思路和分析過程，并非一定是優質題解，重要的是通過分析和解決問題能讓我們逐漸熟練和成長，從新手到大佬離不開一個磨練的過程，加油！

原題鏈接

用對角線遍歷矩陣https://leetcode.cn/leetbook/read/array-and-string/cuxq3/

算法分析

? ? ? ?

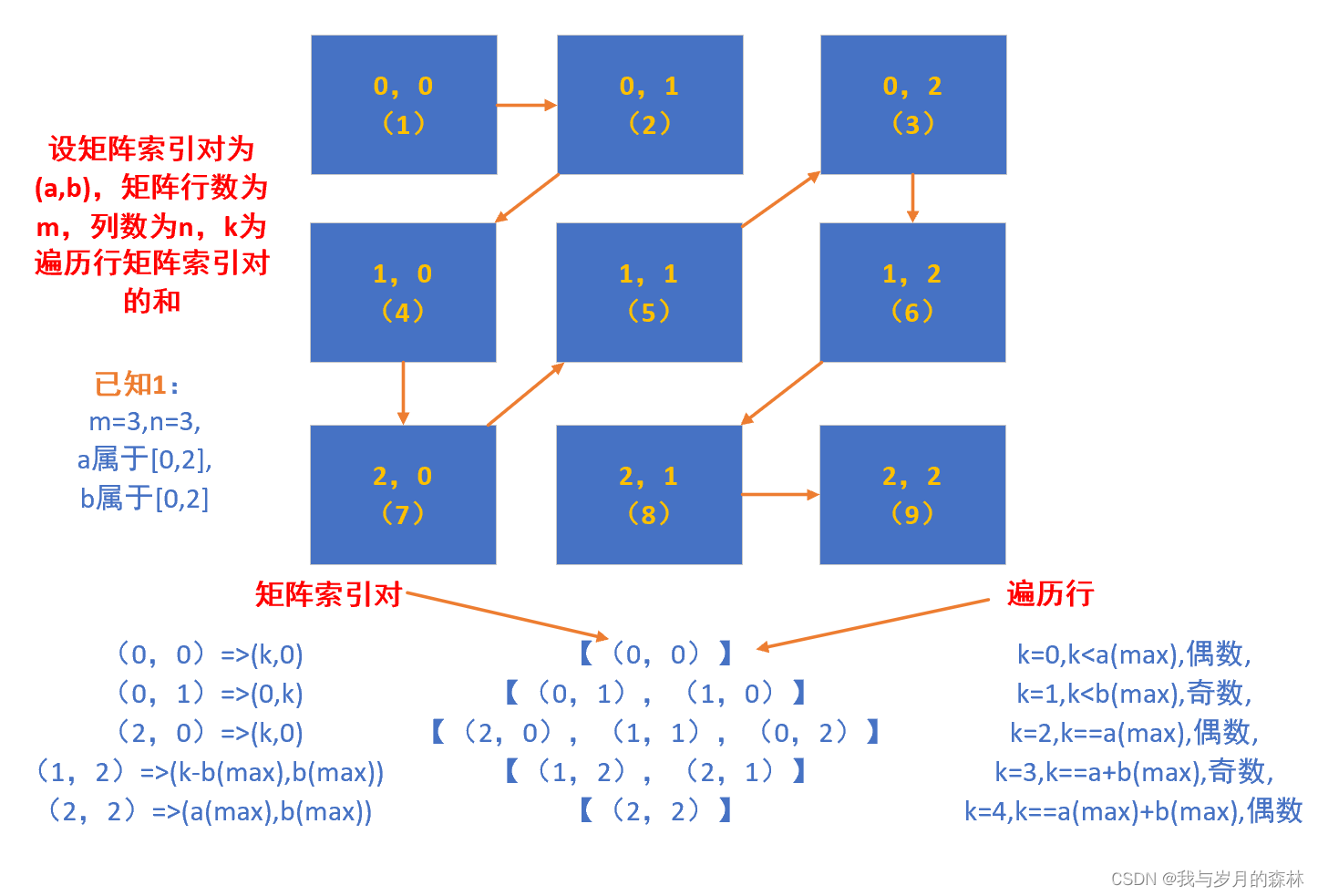
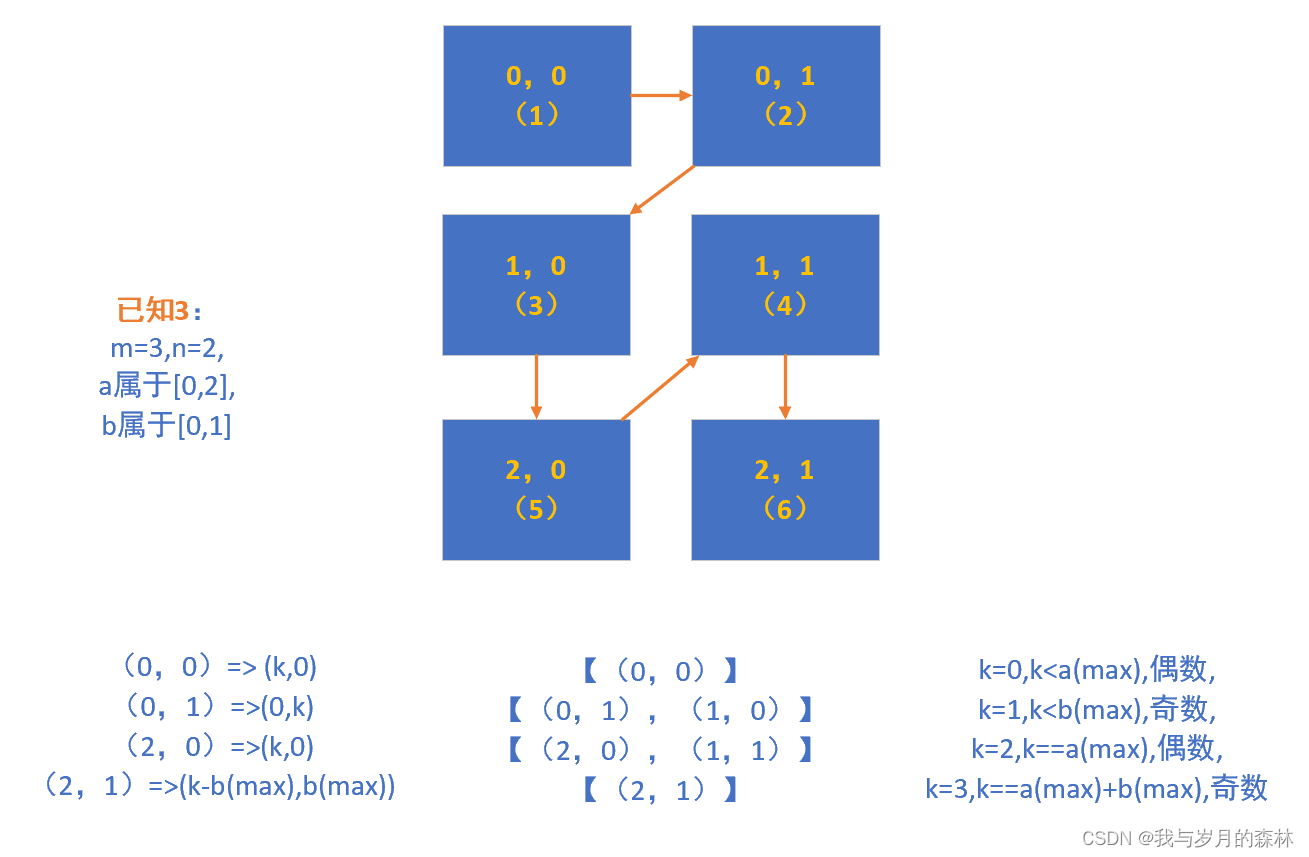
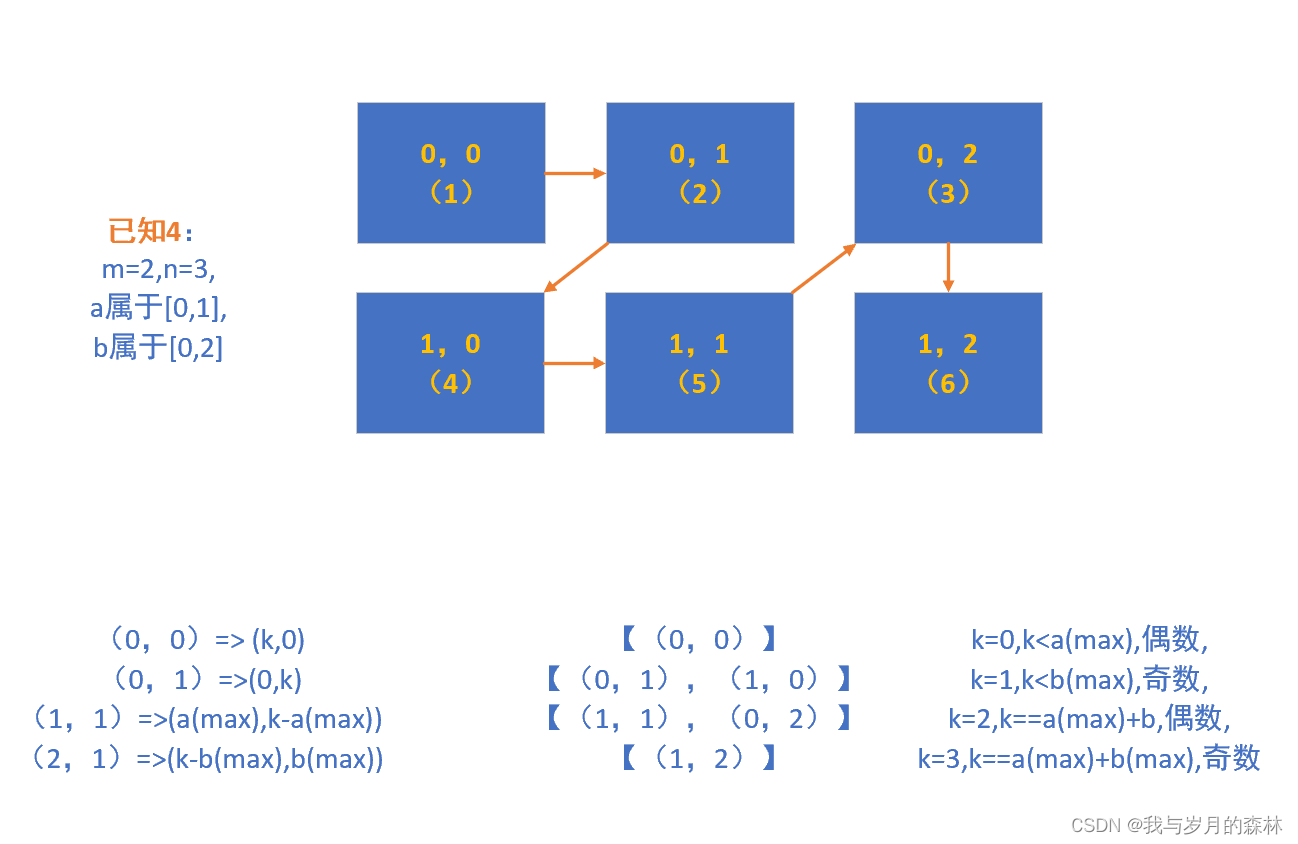
由上述四個圖可以總結得出以下八個結論：?

結論1：k屬于[0,a(max)+b(max)]。

結論2：每一層遍歷行最多存在min(m,n)個矩陣索引對，min(m,n)表示m和n二者中小的那一個值。

結論3：a屬于[0,m-1]，b屬于[0,n-1]。

結論4：若k為偶數則以a為比較對象，此時若k<=a(max)則當前遍歷行的起始索引對為(k,0)，反之則起始索引對為(a(max),k-a(max))。

結論5：若k為奇數則以b為比較對象，此時若k<=b(max)則當前遍歷行的起始索引對位(0,k)，反之則起始索引對為(k-b(max),b(max))。

結論6：從當前遍歷行的起始索引對開始，若k為偶數，則下一個索引對為(a-1,b+1)，反之下一個索引對為(a+1,b-1)。

結論7：遍歷行的結束條件由該矩陣的遍歷行最大索引對個數和a(min)、b(min)共同決定，首先應判斷當前遍歷行訪問的矩陣索引對個數是否達到了該矩陣的遍歷行最大索引對個數，若達到了則完成該遍歷行的遍歷，否則判斷下一個索引對(a,b)，若a或b越界則表明完成該遍歷行的遍歷。

結論8：整個矩陣遍歷結束的條件是當前遍歷的矩陣索引對的個數是m×n個。

?代碼示例（C#）

public int[] FindDiagonalOrder(int[][] mat)
{int m = mat.Length;//矩陣的行數int n = mat[0].Length;//矩陣的列數int[] result = new int[m * n];//結果數組//a:索引對的a,b:索引對的b,k:a+b,count:當前已遍歷的矩陣索引對個數,minA:a的最小值//minB:b的最小值,index:結果數組中的索引指針int a, b, k = 0, count = 0, minA = 0, minB = 0, index = 0;int maxA = m - 1;//a的最大值int maxB = n - 1;//b的最大值int maxIndexsCount = m <= n ? m : n;//該矩陣中遍歷行的矩陣索引對個數的最大值int lineIndexsCount;//遍歷行當前已遍歷的矩陣索引對個數while (count < m * n){lineIndexsCount = 0;//若k%2為0則表示k為偶數，反之則為奇數if (k % 2 == 0){if (k <= maxA){a = k;b = 0;}else{a = maxA;b = k - maxA;}}else{if (k <= maxB){a = 0;b = k;}else{a = k - maxB;b = maxB;}}while (lineIndexsCount < maxIndexsCount){//a或b越界則完成此次遍歷行的遍歷if ((a < minA || a > maxA) || (b < minB || b > maxB)) break;//記錄結果result[index++] = mat[a][b];count++;if (k % 2 == 0){a--;b++;}else{a++;b--;}}k++;}return result;
}

算法解說?

????????按照原題的思路我們列舉出了四種矩陣，嚴格來說只有三種，分別是矩陣行數大于列數、行數等于列數、行數小于列數，而為了保證后續結論的真實性，我們列舉了兩個行數等于列數的矩陣。

????????圖中我們完成了四個矩陣的制定，然后按照題目要求去遍歷了四個矩陣并且將遍歷的結果記錄下來，從行列定義上我們可以將矩陣構建在二維平面中，從而為每一個元素設立一個唯一的坐標值，在本題中我們把這個坐標值稱為索引對。有了索引對我們可以進一步按照索引對兩個數值之和對遍歷結果進行分組，在本題中我們把索引對兩個數值之和相同的一組索引對稱為遍歷行，為了簡便后續將索引對兩個數值之和稱為索引對結果值。

????????將遍歷行按照索引對結果值從小到大的順序進行排列，為了能夠發現更多有用的結論，我們把每一層遍歷行的索引對結果值、結果值的奇偶性、索引對與k值的關系列舉出來，除此之外還需要列舉出矩陣行列數以及索引對兩個數值的取值范圍，至于為什么要去列舉這些東西，實際上還是通過嘗試和思考，就像上學時做數學題，瀏覽題目之后列舉出題目中給定的條件，然后根據條件去解題。

????????這一步我們可以理解為進一步細化和剖析已知條件，我們的目的是從已知條件中獲取可靠的結論，從而根據結論解決問題，因此我們總結出了上文的八個結論。

????????那么已知結論后如何去編寫代碼呢？本人是按照以下幾個問題去解決的。

????????1.我們需要明白輸入和輸出是什么？

????????2.我們需要定義哪些變量？

????????3.函數主體是什么？

????????4.某些過程的結束條件是什么？

????????實際上，就是將我們的八個結論構建為代碼，簡單劃分就是定義變量和邏輯主體，定義變量就看結論中需要記錄數據的描述，邏輯主體就看結論中對于邏輯處理、結束條件的描述。

????????當然這樣轉換出來的代碼比較粗糙，所以后續還可以結合自己的編程知識再去優化自己的代碼，讓它變得更加簡潔精致。