平板涂色

題目描述

CE數碼公司開發了一種名為自動涂色機（APM）的產品。它能用預定的顏色給一塊由不同尺寸且互不覆蓋的矩形構成的平板涂色。

為了涂色，APM需要使用一組刷子。每個刷子涂一種不同的顏色C。APM拿起一把有顏色C的刷子，并給所有顏色為C且符合下面限制的矩形涂色：

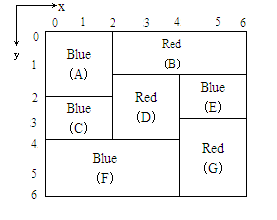
為了避免顏料滲漏使顏色混合，一個矩形只能在所有緊靠它上方的矩形涂色后，才能涂色。例如圖中矩形F必須在C和D涂色后才能涂色。注意，每一個矩形必須立刻涂滿，不能只涂一部分。

寫一個程序求一個使APM拿起刷子次數最少的涂色方案。注意，如果一把刷子被拿起超過一次，則每一次都必須記入總數中。

輸入輸出格式

輸入格式：

第一行為矩形的個數N。下面有N行描述了N個矩形。每個矩形有5個整數描述，左上角的y坐標和x坐標，右下角的y坐標和x坐標，以及預定顏色。

顏色號為1到20的整數。

平板的左上角坐標總是(0, 0)。

坐標的范圍是0..99。

N小于16。?

輸出格式：

文件中記錄拿起刷子的最少次數。

輸入輸出樣例

輸入樣例#1：?

7
0 0 2 2 1
0 2 1 6 2
2 0 4 2 1
1 2 4 4 2
1 4 3 6 1
4 0 6 4 1
3 4 6 6 2

輸出樣例#1：?

3

其實這道題就是一道妥妥的深搜，但還有一群大佬用DP，誒（其實我不打DP是因為，我根本就不會⊙﹏⊙），我們發現這道題有一個坑，如果上面沒有涂，就要先涂上面的。
代碼：

#include<bits/stdc++.h>
using namespace std;
struct str
{int a1,a2,b1,b2,color;
}a[111000];
int b1[11000]={0};//有沒有涂
int b[110][110],n,m,ans=999;
int b2[11000];//顏色數量 
int cmp(str x,str y)//排序 
{if(x.a1!=y.a1) return x.a1<y.a1;//在排橫列 return x.a2<y.a2;//先排縱列
}
bool cha(int x)
{for(int i=0;i<n;i++){if(b[x][i]&&!b1[i]) return false;//上面沒涂,反回false}return true;//反回true
}
void dfs(int x,int ji_lu,int sum)
{if(x>=ans)//如果當前的值大于你要找的值，那就不用找了呢！O(∩_∩)O~~ {return ;}if(sum==n)//涂完了{ans=x;return ;}for(int i=0;i<m;i++)//枚舉每一種顏色 {int h=0;if(b2[i]&&i!=ji_lu)//可以涂，有顏色涂，沒有被涂過 {for(int j=0;j<n;j++){//cha函數判斷上面有沒有被涂（顏色） if(!b1[j]&&a[j].color==i&&cha(j))//如果沒涂過，且能涂 {b1[j]=1;//記錄 h++;}else if(b1[j]&&a[j].color==i) b1[j]++;}if(h>0)//如果被涂了 {dfs(x+1,i,sum+h);//進行下一步 }for(int j=n-1;j>=0;j--)//回溯，不能上色 {if(b1[j]==1&&a[j].color==i&&cha(j)){b1[j]=0;h--;}else if(b1[j]>1&&a[j].color==i){b1[j]--;}}}}
}
int main()
{cin>>n;for(int i=0;i<n;i++){cin>>a[i].a1>>a[i].a2>>a[i].b1>>a[i].b2>>a[i].color;b2[a[i].color]++;//顏色的數量 }m=19;//從零開始 sort(a,a+n,cmp);//應為蒟蒻不會拓撲排序所以先排一下 for(int i=1;i<n;i++){for(int j=i-1;j>=0;j--){if(a[i].a1==a[j].b1&&((a[i].a2>=a[j].a2&&a[i].a2<=a[j].b2)||(a[i].b2>=a[j].a2&&a[i].b2<=a[j].b2))){b[i][j]=1;//如果i塊的最上面，且緊鄰j塊最下面，并且兩磚橫坐標有重疊部分，即i塊為j塊，緊鄰的那塊磚}}}dfs(0,0,0);cout<<ans;
}

　　做完之后，我只想去出題人面前說一句話：午時已到。