引入
我們首先提出一個問題:
給出n個串每個串的長度≤m
然后給出一個長度為k的串,詢問前n個串中有多少個是匹配成了的
暴力搜索
這題不是sb題目嗎?
隨隨便便O(kmn)跑過。
。。。。
n=10000 m=50
k=1000000
。。。。
好吧——我們用AC自動機吧
樣例
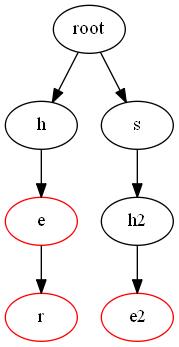
首先我們舉一個例子,我們有n=3個串he 和 her 和 she
然后我們通過構建Trie可以得到下圖
這里紅色的節點到根的路徑可以構成一個串(怎么那么像后綴自動機?)然后我們可以發現
正文
概念
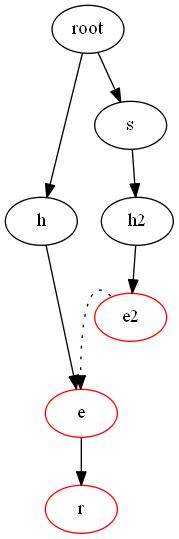
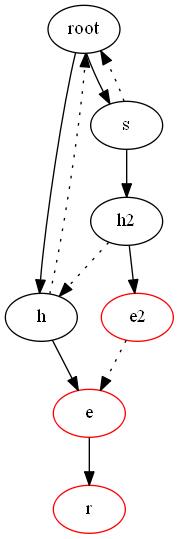
我們使用Fail(i)表示i節點用虛線連接的邊,這樣的邊我們的作用就是當前節點到根的路徑構成的字符串的最長的存在的后綴的串的位置。比如she 和 he 中 he 就是 she 的最長的后綴所以我們連接 e2->e這樣我們假設從e2無法再繼續伸展的時候我們就可以O(1)找到類似的串,然后繼續進行伸展得到如下的圖
這樣比如我們匹配sher的時候我們首先沿著邊走到e2然后不需要重新搜索,而是選擇立即跳轉到e節點然后搜索到r節點
這樣我們就構造出了一個AC自動機的圖
構建方法
就使用上面的例子
對于這樣的一個圖,我們首先隊列中有
| Queue | 0 | 1 |
|---|---|---|
| h | s |
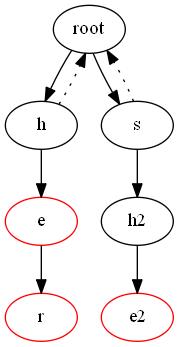
同時將深度為1的節點連接Fail到root
然后我們掃描一遍h節點可以得到e節點然后我們掃描s節點可以發現s的Fail邊上的root節點存在和s的兒子h相同的另一個h那么因為s的fail邊上的所有節點的后綴相同,所以我們有h2和h節點同時增加一個節點后仍然滿足上面的Fail邊的概念,所以我們h2->h得到
同時我們的隊列變成了
| Queue | 0 | 1 |
|---|---|---|
| 2 | h2 |
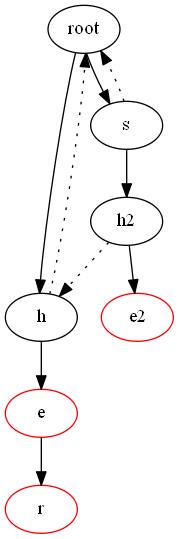
對于下面的伸展我們可以得到(同理):
呵呵呵代碼時間:
代碼
void Insert(char *s){int len = strlen(s), u = root;for(int i=0;i<len;i++){int id = idx(s[i]);if(!pool[u].ch[id]) pool[u].ch[id] = ++ecnt;u = pool[u].ch[id];}pool[u].End_Flag++;
}
void build(){queue<int> que;for(int i=0;i<26;i++)if(pool[root].ch[i])que.push(pool[root].ch[i]);int u, v, t, p;while(!que.empty()){u = que.front();que.pop();for(int i=0;i<MAXK;i++) if(pool[u].ch[i]){v = pool[u].ch[i];que.push(v);p = pool[u].Fail;while(p && !pool[p].ch[i]) p = pool[p].Fail;t = pool[p].ch[i];pool[v].Fail = t;pool[v].last = pool[t].End_Flag ? t : pool[t].last;}}
}感謝
感謝您閱讀這篇文章,如果有不足的地方請做出評論謝謝


)





)






 使用完全解析)



