邊分治講解

前言：

　　邊分治和點分治一樣屬于樹分治的一部分，相比于點分治，邊分治對于與度數相關的問題有著很大的優勢，同時邊分治也是解決樹上最優化問題的一種重要的算法。

分治過程：

　　邊分治的分治過程與點分治類似，同樣每次分治時找到一條分治中心邊使這條邊兩端的兩個聯通塊中較大的一個盡量小。以分治中心邊為界限，恰好將當前分治的聯通塊中的點分成了兩部分，統計路徑經過分治中心邊的答案，然后將分治中心邊斷開，遞歸分治中心邊兩端的兩個聯通塊。

代碼實現：

找分治中心邊

找分治中心邊和找樹的重心方法類似，同樣記錄子樹大小，對于每條邊取這條邊的子節點子樹大小size及聯通塊大小-size中較大的一個更新分治中心邊。代碼中sum為聯通塊大小。

inline void getroot(int x,int fa,int sum)
{size[x]=1;for(int i=head[x];i;i=next[i]){if(!vis[i>>1]&&to[i]!=fa){getroot(to[i],x,sum);size[x]+=size[to[i]];int mx_size=max(size[to[i]],sum-size[to[i]]);if(mx_size<num){num=mx_size;root=i;}}}
}

邊分治

因為我們需要知道分治中心邊的兩端點，所以在開雙向邊時邊的編號要從2開始，這樣x與x^1就是一對雙向邊。代碼中的calc函數是統計經過分治中心邊的答案。

inline void partation(int x,int sum)
{num=INF;getroot(x,0,sum);if(num==INF){return ;}int now=root;vis[now>>1]=1;cnt=0;dfs2(x,0,to[now],1);dfs2(to[now],0,0,2);calc();int sz=size[to[now]];partation(to[now],sz);partation(x,sum-sz);
}

多叉樹轉二叉樹

邊分治的時間復雜度同樣是$O(nlogn)$，但會被菊花圖卡成$O(n^2)$，所以我們要將多叉樹轉成二叉樹，這樣雖然會有一個二倍常數但可以保證時間復雜度是$O(nlogn)$。

多叉樹轉二叉樹的方法有兩種：

1、第一種方法是從1開始枚舉每個點，對于一個點$x$，如果他有<=2個子節點，那么直接向子節點連邊即可；否則新建兩個點，將$x$連向這兩個點，并將$x$的子節點按奇偶分類暫時歸為這兩個新建點的子節點。為了不影響原樹深度等信息，我們將連向新建點的邊權設為0。這樣新建樹因為每條原樹邊會被存$logn$次，所以空間復雜度是$O(nlogn)$，新建節點數$O(n)$。代碼中m為總點數。

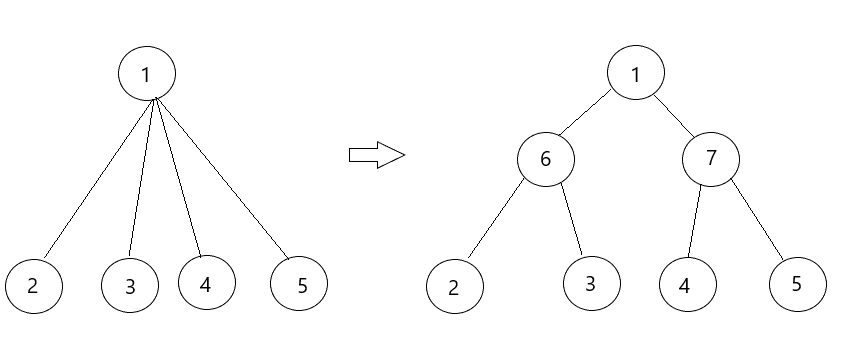
void rebuild()
{tot=1;for(int i=1;i<=n;i++){head[i]=0;}for(int i=1;i<=n;i++){int len=q[i].size();if(len<=2){for(int j=0;j<len;j++){add(i,q[i][j],(q[i][j]<=m));add(q[i][j],i,(q[i][j]<=m));}}else{int ls=++n;int rs=++n;v[ls]=v[rs]=v[i];add(i,ls,0);add(ls,i,0);add(i,rs,0);add(rs,i,0);for(int j=0;j<len;j++){if(j&1){q[ls].push_back(q[i][j]);}else{q[rs].push_back(q[i][j]);}}}}
}

2、第二種方法是dfs整棵樹，對于原樹每個點x，記錄一個$last$(初始為x)，每次將$last$連向一個子節點，并新建一個點$y$將$last$連向$y$，然后將$last$改為$y$。同樣將連向新建點的邊權設為0。因為每個原樹邊只被保存一次，所以空間復雜度是$O(n)$，新建點數是$O(n)$。代碼中m為總點數。

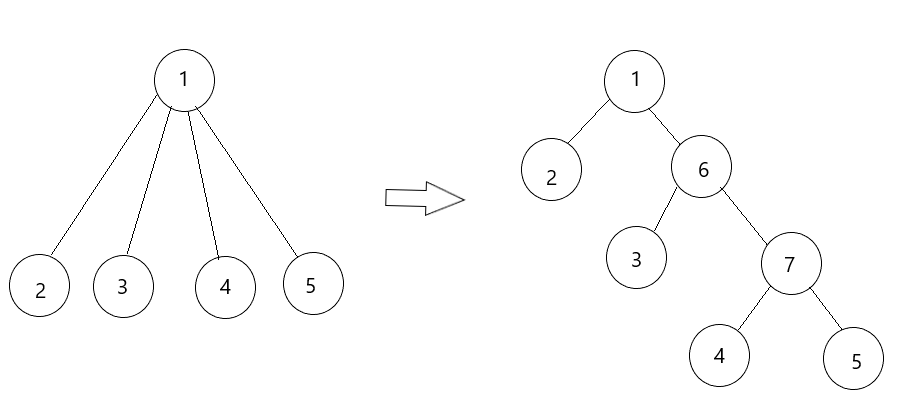
inline void rebuild(int x,int fa)
{int tmp=0;int last=0;int len=v[x].size();for(int i=0;i<len;i++){int to=v[x][i].first;int val=v[x][i].second;if(to==fa){continue;}tmp++;if(tmp==1){add(x,to,val);add(to,x,val);last=x;}else if(tmp==len-(x!=1)){add(last,to,val);add(to,last,val);}else{m++;add(last,m,0);add(m,last,0);last=m;add(m,to,val);add(to,m,val);}}for(int i=0;i<len;i++){if(v[x][i].first==fa){continue;}rebuild(v[x][i].first,x);}
}

邊分治的性質：

1、如果我們在邊分治找中心時以當前聯通塊在原樹中深度最小的點為根，那么找到的分治中心邊在原樹中一定是一條從父節點$u$到子節點$v$的邊，這條邊將當前聯通塊分成了兩部分，可以發現包含$v$的那部分一定是原樹中的一棵子樹，我們假設包含$u$的部分為$S$，包含$v$的部分為$T$，那么$S$中的任意一個點$x$與$T$中的任意一個點$y$的$lca$一定不在$T$中，這也就說明$x$與$T$中所有點的$lca$都相同，就是$lca(x,v)$。

2、邊分治將每次的分治聯通塊中的點恰好分成了兩部分，這就省去了像點分治那樣單獨處理以分治重心為路徑端點的答案這一過程。

邊分樹：

與點分樹類似，我們將每層分治中心邊連向下一層的分治中心邊所形成的樹就是邊分樹，邊分樹是一棵二叉樹，它可以類似線段樹一樣合并，這一部分內容暫時還不完整，待博主后續更新。

練習題：

BZOJ2870最長道路(邊分治模板題)

CSTC2018暴力寫掛(兩棵樹，第一棵樹邊分治轉到第二棵樹上建虛樹DP)

WC2018通道(三棵樹，碼量較大)