半數集問題

　　給定一個自然數n，由n開始可以依次產生半數集set(n)中的數如下：

　　(1)???n?∈set(n)；

　　(2)?在n的左邊加上一個自然數，但該自然數不能超過最近添加的數的一半；

　　(3)?按此規則進行處理，直到不能再添加自然數為止。

　　以6為例子，6，6前面可以加1，2，3生成16，26，36，26前面可以加1生成126，同理36生成136.所以6的半數集元素個數為6分別是6，16，26，36，126，136

　　以12為例子，只加一個數字產生的元素有612，512，412，312，212，112。因為之后加的數字與‘12’沒有關系，只與第一次加的數字有關，612，512，412，312，212，112產生的半數集元素的個數相當于6，5，4，3，2，1的半數集的個數，不難得到如下公式。

　　

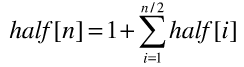
遞歸代碼：

#include <algorithm>
#include <iostream>
#include <cstring>
#include <vector>
#include <cstdio>using namespace std;int f(int n){if(n==1)return 1;else{int ans=1;for(int i=1;i<=n/2;i++){ans=ans+f(i);}return ans;}
}int main()
{int n;scanf("%d",&n);int num=f(n);printf("%d\n",num);return 0;
}

　　遞歸時間復雜度很高對此我們可以進行優化，用數組空間存儲之前的狀態

O（n²）實現：

#include <algorithm>
#include <iostream>
#include <cstring>
#include <vector>
#include <cstdio>using namespace std;int main()
{int n;scanf("%d",&n);int a[100];a[1]=1;for(int i=2;i<=n;i++){a[i]=1;for(int j=1;j<=i/2;j++){a[i]+=a[j];}}printf("%d\n",a[n]);return 0;
}

　　仔細分析后，發現時間復雜度其實可以降到O（n），因為當n為奇數時，第n項的半數集個數等于第n-1項的半數集個數，當n為偶數時，第n項的半數集個數等于第n-1項半數集個數 加 第n/2項半數集個數。

O（n）實現：

#include <algorithm>
#include <iostream>
#include <cstring>
#include <vector>
#include <cstdio>using namespace std;int main()
{int n;scanf("%d",&n);int a[100];a[0]=a[1]=1;for(int i=2;i<=n;i++){if(i%2!=0)a[i]=a[i-1];else{a[i]=a[i-1]+a[i/2];}}printf("%d\n",a[n]);return 0;
}