PCA(Principal Component Analysis),即主成分分析,一種常用于數據降維分析的方法。要理解PCA的原理,首先需要理解矩陣變換的意義。
矩陣變換,有兩種意義:1,在當前坐標系下的向量,經過矩陣M變換后,結果為被變換的向量在當前坐標系下的新向量。
2,保持向量不變,矩陣M對當前坐標系進行變換,結果為當前向量在新坐標系下的向量表示。該新坐標系即矩陣M,變換后的向量是在新坐標系下各坐標軸上的投影。
以二維空間樣本為例,有如下一批樣本:

我們需要將該二維樣本數據轉換到一維空間中,只分析一維空間樣本數據。如果我們直接在當前坐標系下分析該樣本,把所有樣本投影到X或者Y軸的任意一個一維空間上,樣本數據都會有較大的損失。如果我們能夠找到一個變換矩陣M,使得當前坐標系旋轉到下圖X' Y'位置:
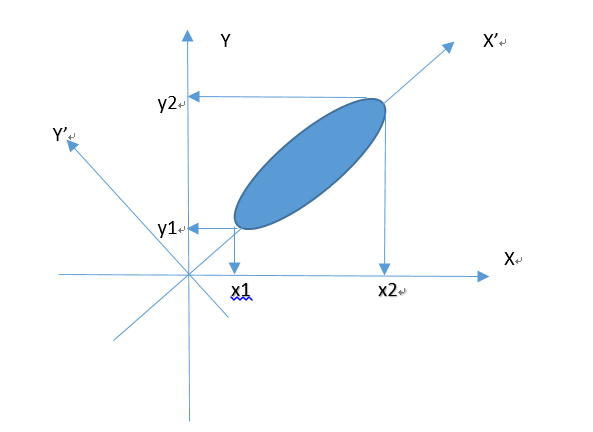
此時,所有樣本數據在X'坐標軸上的投影達到最大,分散的最開。因此直觀上X' Y'坐標系就是我們需要尋找的最優變換M。
如何得到這個變換矩陣M?假設我們有如上圖一組樣本數據A=(x,y),經過矩陣M變換后,樣本數據在M坐標系下的投影變成了B=(x',y')。下面分析如何得到M:
(1)首先我們對樣本做一次歸一化處理(每個樣本數據減去相應的樣本均值)。這么處理的好處主要是方便后續計算樣本方差和協方差。處理后的樣本分布如下圖所示:
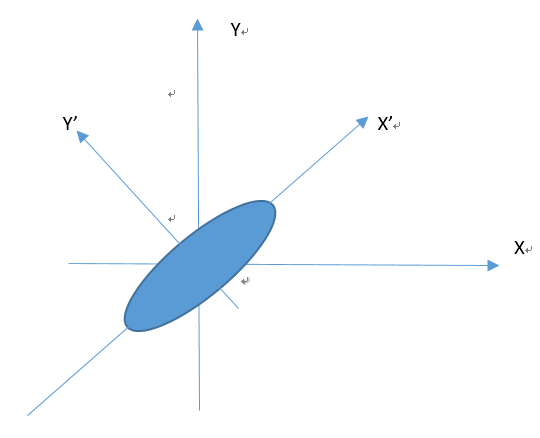
(2)所以我們的目標是使得變換后的單個樣本數據B在X' Y'上的投影最分散和最大化,也就是使得B=(x', y')中 |x'|或者|y'|最大,而 x'y' 趨近于0。進一步,所有樣本數據,使得
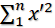 或者??
或者??
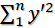 最大化,而
最大化,而
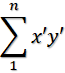 趨近于0。
趨近于0。
對樣本數據A=(x,y)來說,令C=
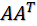 ,對變換后的樣本數據B=(x',y')來說,令D=
,對變換后的樣本數據B=(x',y')來說,令D=
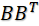 。那么,C和D的矩陣表示如下:
。那么,C和D的矩陣表示如下:
C=(
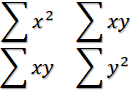 )? ? D=(
)? ? D=(
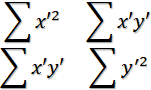 )
)
可以看到C和D的主對角線上的元素就是(x,y)和(x',y')的方差。而非主對角線上元素就是(x,y)和(x',y')的協方差。這個C和D被稱為C和D的協方差矩陣。
現在我們的目標是找到變換矩陣M,使得協方差矩陣D對角化。
(3)那么C,D和M是什么關系呢?

上式表明我們的目標變成:尋找一個變換矩陣M,使得MC
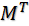 是一個對角矩陣。
是一個對角矩陣。
又已知C是一個對稱矩陣,由對稱矩陣的性質可知,一定存在一組C的特征向量作為行組成的特征矩陣E,使得
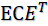 =F,其中F是對角矩陣。
=F,其中F是對角矩陣。
結論:這與我們的目標一致,我們要尋找的PCA變換矩陣M就是E,也就是原始樣本數據A的協方差矩陣C的特征向量作為行組成的特征矩陣。
那么,下面我們總結一下PCA的步驟:
(1)樣本數據歸一化處理
(2)對歸一化后的樣本數據求出協方差矩陣C
(3)對協方差矩陣C求出其特征向量和特征值
(4)以特征值大小按行排列相應的特征向量,舍棄特征值較小的特征向量行,組成的矩陣就是需要找尋的降維后的變換矩陣M。
)



)



)
...)


)



)


