440. 字典序的第K小數字
給定整數 n 和 k,找到 1 到 n 中字典序第 k 小的數字。
注意:1 ≤ k ≤ n ≤ 109。
示例 :
輸入:
n: 13 k: 2
輸出:
10
解釋:
字典序的排列是 [1, 10, 11, 12, 13, 2, 3, 4, 5, 6, 7, 8, 9],所以第二小的數字是 10。
解題思路
N個數字可以組織成為具有n個節點的10叉樹,該樹的前序遍歷就是數字的字典序,如圖所示
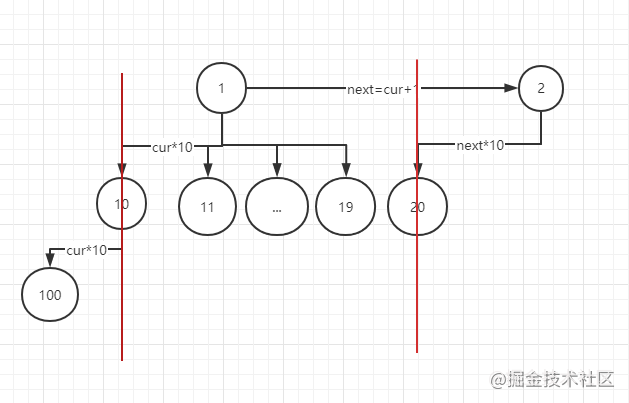
我們的目標就是需要找前序遍歷的第k個節點
我們可以選擇性的選擇父節點遍歷,不需要遍歷前k個節點。
例如
輸入:
n: 13 k: 6輸出:
2解釋:
字典序的排列是 [1, 10, 11, 12, 13, 2, 3, 4, 5, 6, 7, 8, 9],所以第六小的數字是 2。
我們可以通過計算出,以1開頭有多少個節點,對比和k的關系。
- 以1為根節點的子樹節點數量為5,如果k為6,說明不需要遍歷以1為根節點的樹,直接向左移動到以2為根節點的樹上,繼續遍歷
- 以1為根節點的子樹節點數量為5,如果k為2,說明我們需要遍歷的節點必然在根節點1的子樹上面,我們移動到根節點的最左子節點,繼續遍歷
如何計算子樹的節點樹
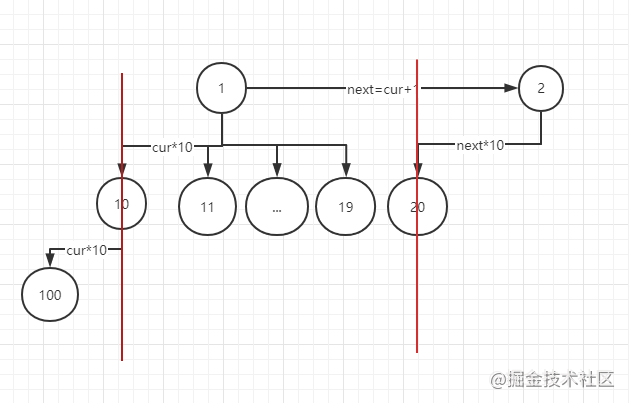
從上圖可以觀察出,每一層節點的數字都是單調遞增的,例如10,11…19,20,因此我們通過計算根節點的最左節點來固定每一層的節點數
每一層我們需要計算的節點數,位于上圖紅線劃分的區間中。
代碼
class Solution {public int findKthNumber(int n, int k) {long cur=1;k--;while (k>0){int number = findingKthNumber(n, cur);if (k>=number){k-=number;cur++;}else {k--;cur*=10;}}return (int)cur;}//sum 上一層的數字public int findingKthNumber(int n, long cur) {long next=cur+1;long res=0;while (cur<=n){res+= Math.min(n-cur+1,next-cur);cur*=10;next*=10;}return (int)res;}
}

















映射)

