【題目描述】
Now you get a number N, and a M-integers set, you should find out how many integers which are small than N, that they can divided exactly by any integers in the set. For example, N=12, and M-integer set is {2,3}, so there is another set {2,3,4,6,8,9,10}, all the integers of the set can be divided exactly by 2 or 3. As a result, you just output the number 7.
Input
There are a lot of cases. For each case, the first line contains two integers N and M. The follow line contains the M integers, and all of them are different from each other. 0<N<2^31,0<M<=10, and the M integer are non-negative and won’t exceed 20.
Output
For each case, output the number.
Sample Input

12 2
2 3

Sample Output

7

【題目分析】
首先我們需要學習一下容斥原理，不懂的話可以移步去看一下這篇大佬的博客：傳送門
里面講的很詳細，除去證明之類的，我覺得比較重要的是容斥原理的公式

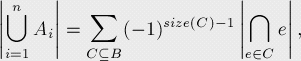
emm，看起來可能不太像人話，翻譯一下就是幾個集合的并集的元素的個數等于每個集合的個數減去集合兩兩相交的集合的元素的個數加上集合三三相交的集合的元素的個數……
然后我們就能解決這個問題啦，因為想求的是$(0,n)$內能被集合內元素整除的數的個數，我們把每個元素整除的數看作一個集合，那么我們想求的就是這些集合并集的元素的個數。而每個元素的個數挺好求的，就是(n-1)/元素的最小公倍數。
然后我們進行枚舉就可以啦，只是直接枚舉的話得需要用dfs稍微有些麻煩，我們用二進制枚舉進行優化。
$PS:$題目說的是非負數，所以說有可能含0，注意讀入的時候將0濾去。而且數字最大為n-1，取不到n

【AC代碼】

#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<algorithm>
#include<iostream>
#include<cmath>
#include<climits>
#include<queue>
#include<vector>
#include<set>
#include<map>
using namespace std;typedef long long ll;
const int MAXN=15;
int a[MAXN];
int n,m,r;
int ans,sign,t;int gcd(int a,int b)
{return a%b==0?b:gcd(b,a%b);
}int main()
{while(~scanf("%d%d",&n,&m)){r=n-1;ans=0;int h=0;for(int i=0;i<m;i++){scanf("%d",&a[h]);if(a[h]) h++;}m=h;for(int i=1,limit=1<<m;i<limit;i++){sign=0; t=1;for(int j=0;j<m;j++){if(i&(1<<j)){sign++;t=a[j]/gcd(a[j],t)*t;}}if(sign%2){ans+=r/t;}else{ans-=r/t;}}printf("%d\n",ans);}return 0;
}