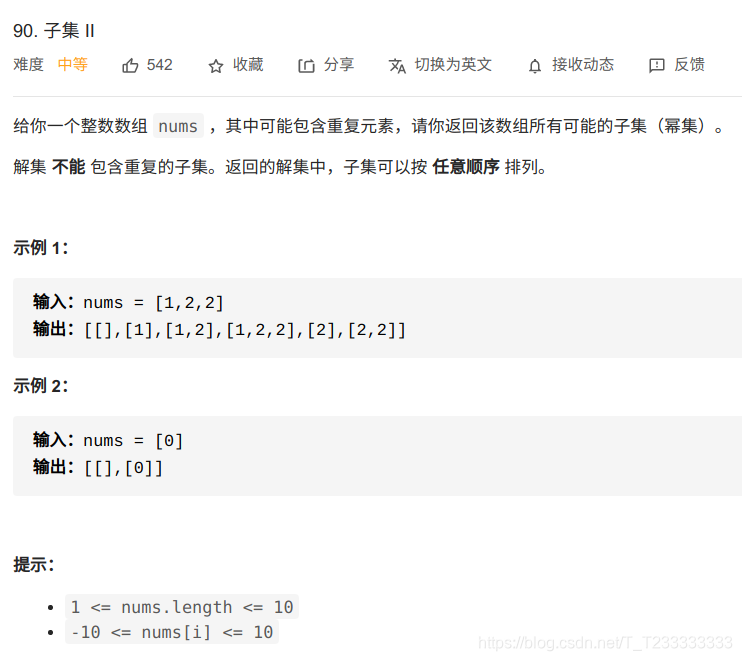
題目描述

題目分析

感覺這道題讓自己對枚舉排列有了一個更好的認識，感覺自己的這種思路不錯。

假設沒有重復元素（退化成78.子集），我們應該怎么做？初始的時候冪集中只有一個空集，然后對每個元素，我們添加給冪集中的每個元素，這樣進行一遍遍歷，復雜度是$O(1)+O(2)+O(4)+...+O(2^{n?1})=O(2^n)$

對于有重復元素的我們應該如何處理呢？不難發現，假設我們把重復元素放在一起，則對于第一個元素是沒有什么影響的，但是對第二個元素開始，我們對冪集最前面集合添加元素和前面的那個元素沒有區別，因此就會出現重復，從哪里開始不一樣呢？從前一個元素開始添加的部分開始，因此我們用一個變量記錄前一個元素開始添加的位置，然后從重復元素的第二個開始都從前一個元素添加的開始位置開始添加，最后更新這個變量。可以再對照代碼理解一下，代碼比較簡單

class Solution {
public:vector<vector<int>> subsetsWithDup(vector<int>& nums) {sort(nums.begin(), nums.end());vector<vector<int>> ans;ans.push_back(vector<int>());ans.push_back(vector<int>());ans.back().push_back(nums[0]);int n = nums.size();int pre_i = 1; //保存上次添加后的起始地址for(int i = 1; i < n; ++i) {int m = ans.size();int j = 0;if (nums[i] == nums[i - 1]) {//如果和上一個數字一樣，則從上一個數字開始的地方開始，因為前面的已經由上一個數字處理過了j = pre_i;}for (; j < m; ++j) {auto t = ans[j];t.push_back(nums[i]);ans.push_back(t);}pre_i = m;      //更新per_i}return ans;}
};

吐槽

覺得子集的思路比題解的要清晰，復雜度應該也低很多，我這個應該是$O(2^n)$，不知道為什么題解的那么復雜，要枚舉二進制或者用回溯。

這個執行用時有點玄學的，可能只測試了部分樣例吧，畢竟是企業，少測試一會就可以多賺錢，可以理解。我覺得leetcode還是比較適合用來學習算法和數據結構的，感覺寫官方題解的人的水平也不一樣，有的題解思路清晰，代碼巧妙，能從代碼中看出寫這個代碼的人造詣很高，對語言的理解也很深刻，但是今天的這個題解我就覺得不怎么樣，子集那道題的題解我也覺得不怎么樣，復雜度感覺都求錯了。