???《博主簡介》

小伙伴們好，我是阿旭。專注于人工智能AI、python、計算機視覺相關分享研究。
?更多學習資源，可關注公-仲-hao:【阿旭算法與機器學習】，共同學習交流~
👍感謝小伙伴們點贊、關注！

《------往期經典推薦------》

一、AI應用軟件開發實戰專欄【鏈接】
二、機器學習實戰專欄【鏈接】，已更新31期，歡迎關注，持續更新中~~
三、深度學習【Pytorch】專欄【鏈接】
四、【Stable Diffusion繪畫系列】專欄【鏈接】

布隆過濾器（Bloom Filter）是一個占用空間很小、效率很高的隨機數據結構，它由一個bit數組和一組Hash算法構成。可用于判斷一個元素是否在一個集合中，查詢效率很高（1-N，最優能逼近于1）。

在很多場景下，我們都需要一個能迅速判斷一個元素是否在一個集合中。譬如：

網頁爬蟲對URL的去重，避免爬取相同的URL地址；

反垃圾郵件，從數十億個垃圾郵件列表中判斷某郵箱是否垃圾郵箱（同理，垃圾短信）；

緩存擊穿，將已存在的緩存放到布隆中，當黑客訪問不存在的緩存時迅速返回避免緩存及DB掛掉。

可能有人會問，我們直接把這些數據都放到數據庫或者redis之類的緩存中不就行了，查詢時直接匹配不就OK了？

是的，當這個集合量比較小，你內存又夠大時，是可以這樣做，你可以直接弄個HashSet、HashMap就OK了。但是當這個量以數十億計，內存裝不下，數據庫檢索極慢時該怎么辦。

以垃圾郵箱為例

方案比較

1.將所有垃圾郵箱地址存到數據庫，匹配時遍歷

2.用HashSet存儲所有地址，匹配時接近O（1）的效率查出來

3.將地址用MD5算法或其他單向映射算法計算后存入HashSet，無論地址多大，保存的只有MD5后的固定位數

4.布隆過濾器，將所有地址經過多個Hash算法，映射到一個bit數組；怎么判斷一個外來的元素是否已經在集合里呢？如果映射的元素的中包含0，則該元素一定不在集合里，如果該元素映射的都為1，那么該元素可能在數組里。

優缺點

方案1和2都是保存完整的地址，占用空間大。一個地址16字節，10億即可達到上百G的內存。HashSet效率逼近O(1)，數據庫就不談效率了，不在一個數量級。

方案3保存部分信息，占用空間小于存儲完整信息，存在沖突的可能（非垃圾郵箱可能MD5后和某垃圾郵箱一樣，概率低）

方案4將所有地址經過Hash后映射到?同一個bit數組，看清了，只有一個超大的bit數組，保存所有的映射，占用空間極小，沖突概率高。

大家知道，java中的HashMap有個擴容參數默認是0.75，也就是你想存75個數，至少需要一個100的數組，而且還會有不少的沖突。實際上，Hash的存儲效率是0.5左右，存5個數需要10個的空間。算起來占用空間還是挺大的。

而布隆過濾器就不用為每個數都分配空間了，而是直接把所有的數通過算法映射到同一個數組，帶來的問題就是沖突上升，只要概率在可以接受的范圍，用時間換空間，在很多時候是好方案。布隆過濾器需要的空間僅為HashMap的1/8-1/4之間，而且它不會漏掉任何一個在黑名單的可疑對象，問題只是會誤傷一些非黑名單對象。

原理

經過K個哈希算法將每個算法將元素映射到數組中的位置標1；

初始化狀態是一個全為0的bit數組

?

為了表達存儲N個元素的集合，使用K個獨立的函數來進行哈希運算。x1，x2……xk為k個哈希算法。

如果集合元素有N1，N2……NN，N1經過x1運算后得到的結果映射的位置標1，經過x2運算后結果映射也標1，已經為1的1保持不變。經過k次散列后，對N1的散列完成。

依次對N2，NN等所有數據進行散列，最終得到一個部分為1，部分位為0的字節數組。當然了，這個字節數組會比較長，不然散列效果不好。

那么怎么判斷一個外來的元素是否已經在集合里呢，譬如已經散列了10億個垃圾郵箱，現在來了一個郵箱，怎么判斷它是否在這10億里面呢？

很簡單，就拿這個新來的也依次經歷x1，x2……xk個哈希算法即可。

在任何一個哈希算法譬如到x2時，得到的映射值有0，那就說明這個郵箱肯定不在這10億內。

如果是一個黑名單對象，那么可以肯定的是所有映射都為1，肯定跑不了它。也就是說是壞人，一定會被抓。

那么誤傷是為什么呢，就是指一些非黑名單對象的值經過k次哈希后，也全部為1，但它確實不是黑名單里的值，這種概率是存在的，但是是可控的。

什么情況下需要布隆過濾器？

先來看幾個比較常見的例子

• 字處理軟件中，需要檢查一個英語單詞是否拼寫正確
• 在 FBI，一個嫌疑人的名字是否已經在嫌疑名單上
• 在網絡爬蟲里，一個網址是否被訪問過
• yahoo, gmail等郵箱垃圾郵件過濾功能

這幾個例子有一個共同的特點：?如何判斷一個元素是否存在一個集合中？

常規思路

• 數組
• 鏈表
• 樹、平衡二叉樹、Trie
• Map (紅黑樹)
• 哈希表

雖然上面描述的這幾種數據結構配合常見的排序、二分搜索可以快速高效的處理絕大部分判斷元素是否存在集合中的需求。但是當集合里面的元素數量足夠大，如果有500萬條記錄甚至1億條記錄呢？這個時候常規的數據結構的問題就凸顯出來了。數組、鏈表、樹等數據結構會存儲元素的內容，一旦數據量過大，消耗的內存也會呈現線性增長，最終達到瓶頸。有的同學可能會問，哈希表不是效率很高嗎？查詢效率可以達到O(1)。但是哈希表需要消耗的內存依然很高。使用哈希表存儲一億 個垃圾 email 地址的消耗？哈希表的做法：首先，哈希函數將一個email地址映射成8字節信息指紋；考慮到哈希表存儲效率通常小于50%（哈希沖突）；因此消耗的內存：8 * 2 * 1億 字節 = 1.6G 內存，普通計算機是無法提供如此大的內存。這個時候，布隆過濾器（Bloom Filter）就應運而生。在繼續介紹布隆過濾器的原理時，先講解下關于哈希函數的預備知識。

哈希函數

哈希函數的概念是：將任意大小的數據轉換成特定大小的數據的函數，轉換后的數據稱為哈希值或哈希編碼。下面是一幅示意圖：

可以明顯的看到，原始數據經過哈希函數的映射后稱為了一個個的哈希編碼，數據得到壓縮。哈希函數是實現哈希表和布隆過濾器的基礎。

布隆過濾器介紹

• 巴頓.布隆于一九七零年提出
• 一個很長的二進制向量 （位數組）
• 一系列隨機函數 (哈希)
• 空間效率和查詢效率高
• 有一定的誤判率（哈希表是精確匹配）

布隆過濾器原理

布隆過濾器（Bloom Filter）的核心實現是一個超大的位數組和幾個哈希函數。假設位數組的長度為m，哈希函數的個數為k

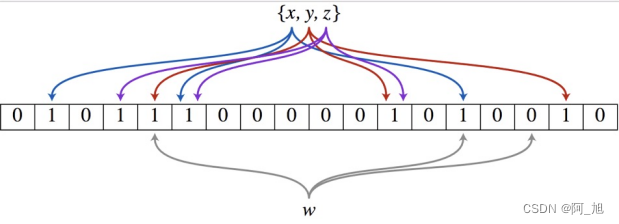
以上圖為例，具體的操作流程：假設集合里面有3個元素{x, y, z}，哈希函數的個數為3。首先將位數組進行初始化，將里面每個位都設置位0。對于集合里面的每一個元素，將元素依次通過3個哈希函數進行映射，每次映射都會產生一個哈希值，這個值對應位數組上面的一個點，然后將位數組對應的位置標記為1。查詢W元素是否存在集合中的時候，同樣的方法將W通過哈希映射到位數組上的3個點。如果3個點的其中有一個點不為1，則可以判斷該元素一定不存在集合中。反之，如果3個點都為1，則該元素可能存在集合中。注意：此處不能判斷該元素是否一定存在集合中，可能存在一定的誤判率。可以從圖中可以看到：假設某個元素通過映射對應下標為4，5，6這3個點。雖然這3個點都為1，但是很明顯這3個點是不同元素經過哈希得到的位置，因此這種情況說明元素雖然不在集合中，也可能對應的都是1，這是誤判率存在的原因。

布隆過濾器添加元素

• 將要添加的元素給k個哈希函數
• 得到對應于位數組上的k個位置
• 將這k個位置設為1

布隆過濾器查詢元素

• 將要查詢的元素給k個哈希函數
• 得到對應于位數組上的k個位置
• 如果k個位置有一個為0，則肯定不在集合中
• 如果k個位置全部為1，則可能在集合中

布隆過濾器實現

import?mmh3 from?bitarray import?bitarray # zhihu_crawler.bloom_filter # Implement a simple bloom filter with murmurhash algorithm. # Bloom filter is used to check wether an element exists in a collection, and it has a good performance in big data situation. # It may has positive rate depend on hash functions and elements count. BIT_SIZE =?5000000 class?BloomFilter: ???? ????def?__init__(self): ????????# Initialize bloom filter, set size and all bits to 0 ????????bit_array =?bitarray(BIT_SIZE) ????????bit_array.setall(0) ????????self.bit_array =?bit_array ???????? ????def?add(self,?url): ????????# Add a url, and set points in bitarray to 1 (Points count is equal to hash funcs count.) ????????# Here use 7 hash functions. ????????point_list =?self.get_postions(url) ????????for?b in?point_list: ????????????self.bit_array[b]?=?1 ????def?contains(self,?url): ????????# Check if a url is in a collection ????????point_list =?self.get_postions(url) ????????result =?True ????????for?b in?point_list: ????????????result =?result and?self.bit_array[b] ???? ????????return?result ????def?get_postions(self,?url): ????????# Get points positions in bit vector. ????????point1 =?mmh3.hash(url,?41)?%?BIT_SIZE ????????point2 =?mmh3.hash(url,?42)?%?BIT_SIZE ????????point3 =?mmh3.hash(url,?43)?%?BIT_SIZE ????????point4 =?mmh3.hash(url,?44)?%?BIT_SIZE ????????point5 =?mmh3.hash(url,?45)?%?BIT_SIZE ????????point6 =?mmh3.hash(url,?46)?%?BIT_SIZE ????????point7 =?mmh3.hash(url,?47)?%?BIT_SIZE ????????return?[point1,?point2,?point3,?point4,?point5,?point6,?point7]

關于本篇文章大家有任何建議或意見，歡迎在評論區留言交流！

覺得不錯的小伙伴，感謝點贊、關注加收藏哦！

歡迎關注下方GZH：阿旭算法與機器學習，共同學習交流~