參考文章：https://github.com/CyC2018/CS-Notes/blob/master/notes/Leetcode%20%E9%A2%98%E8%A7%A3%20-%20%E6%90%9C%E7%B4%A2.md

廣度優先搜索（BFS）

廣度優先搜索是按層來處理頂點的，距離開始點最近的那些頂點首先被訪問，而最遠的那些頂點則最后被訪問。BFS的代碼使用了一個隊列。搜索的步驟：

首先選擇一個頂點作為起始頂點，將起始頂點放入隊列中
從隊列首部選出一個頂點，將與之相鄰并且沒有被訪問的結點依次加入到隊列的隊尾，然后訪問這些與之相鄰并且沒有被訪問過的結點，將隊列隊首的結點刪去。
按照步驟2處理隊列中下一個結點，直到找到要找的結點或者隊列中沒有結點結束。

void BFS()
{定義隊列;定義備忘錄，用于記錄已經訪問的位置；判斷邊界條件，是否能直接返回結果的。將起始位置加入到隊列中，同時更新備忘錄。while (隊列不為空) {獲取當前隊列中的元素個數。for (元素個數) {取出一個位置節點。判斷是否到達終點位置。獲取它對應的下一個所有的節點。條件判斷，過濾掉不符合條件的位置。新位置重新加入隊列。}}}

我們用一道LeedCode上面的題目講解，題目位置：

https://leetcode-cn.com/problems/shortest-path-in-binary-matrix/
這里我們需要注意三點：

需要一個隊列，來記錄下一次訪問的結點，因為該隊列是記錄結點位置的（訪問結點的下標），如果一維數組可以搞定，定義個int queue[QUEUE_SIZE]，如果是二維，定義int queue[QUEUW_SIZE][2].
需要一個備忘錄，記錄已經被訪問的結點，備忘錄用數組表示
每一層結點數就是可以訪問的結點，這里題目是 8 個方向上的單元格

#include <stdio.h>
#include <string.h>
#include <stdlib.h>#define QUEUE_SIZE 10001
int BFS()
{int grid[3][3] = {{0,0,0},{1,1,0},{1,1,0}};int gridSize=3;int ans=0; /*判斷邊界條件，即結束條件*/if(grid[gridSize-1][gridSize-1]==1 || grid[0][0]==1)return -1;/* 獲取隊列 */if(gridSize==1)return 1;int m=gridSize,n=m*m,front=0,rear=0,pre_rear=0,cnt=1;/* 設置隊列 */ int **cularr = (int **)malloc(sizeof(int)*n);for(int i=0;i<n;i++){cularr[i]=(int *)malloc(sizeof(int)*2);}/* 將首結點入隊 并將其設置已經訪問過了*/cularr[rear][0]=0;cularr[rear++][1]=0;/*將其修改為1  表示這個數據不需要在訪問 */grid[0][0]=1;/* 根據題目要求廣度優先都要有8個結點 */int temp[8][2] = {{-1,-1},{0,-1},{1,-1},{1,0},{1,1},{0,1},{-1,1},{-1,0}};while(front<rear){pre_rear = rear;/* 遍歷每一層上的結點 */while(front<pre_rear){for(int i=0;i<8;i++){int x = cularr[front][0]+temp[i][0];int y = cularr[front][1]+temp[i][1];//此時是最后一個結點if((m-1==x)&&(m-1==y)){return cnt+1;}//將沒有訪問符合的符合條件的加入隊列中if(x<m && x>=0 && y<m && y>=0 && grid[x][y]==0){cularr[rear][0]=x;cularr[rear++][1]=y;grid[x][y]=1;}}front++;   //獲取下一個隊首元素}cnt++;     //廣度優先遍歷了一層，要加1}return -1;}int main(void)
{int num = BFS();printf("%d\n",num);return 0;
}

深度優先遍歷（DFS）

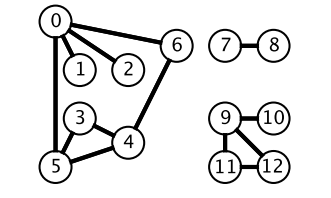
在這里插入圖片描述

廣度優先搜索一層一層遍歷，每一層得到的所有新節點，要用隊列存儲起來以備下一層遍歷的時候再遍歷。

而深度優先搜索在得到一個新節點時立即對新節點進行遍歷：從節點 0 出發開始遍歷，得到到新節點 6 時，立馬對新節點 6 進行遍歷，得到新節點 4；如此反復以這種方式遍歷新節點，直到沒有新節點了，此時返回。返回到根節點 0 的情況是，繼續對根節點 0 進行遍歷，得到新節點 2，然后繼續以上步驟。

從一個節點出發，使用 DFS 對一個圖進行遍歷時，能夠遍歷到的節點都是從初始節點可達的，DFS 常用來求解這種 可達性 問題。

在程序實現 DFS 時需要考慮以下問題：

棧：用棧來保存當前節點信息，當遍歷新節點返回時能夠繼續遍歷當前節點。可以使用遞歸棧。
標記：和 BFS 一樣同樣需要對已經遍歷過的節點進行標記。
每個結點有多少個子樹（也就是一個結點遍歷完，深度優先遍歷時，有幾個可選的結點可以遍歷，比如上圖的0，可以有1、2、5、6四個結點可以選擇）

我們用LeedCode上面的題目來講解：

695. 島嶼的最大面積

#include <stdio.h>
#include <stdlib.h>int dfs(int **grid,int gridSize,int *gridColSize,int row,int col)
{//條件判斷if(row<0 || row>=gridSize || col<0 || col>=gridColSize[0] || grid[row][col]==0){return 0;}//將1置為0，表示已經訪問過該結點grid[row][col]=0;//遍歷所有可以遍歷的情況return 1+dfs(grid,gridSize,gridColSize,row,col+1)+dfs(grid,gridSize,gridColSize,row,col-1)+dfs(grid,gridSize,gridColSize,row+1,col)+dfs(grid,gridSize,gridColSize,row-1,col);
}int maxAreaOfIsland(int** grid, int gridSize, int* gridColSize) 
{int area=0,max=0,i,j;for(i=0;i<gridSize;i++){for(j=0;j<gridColSize[0];j++){area = dfs(grid,gridSize,gridColSize,i,j);max = max>area?max:area;}}return max;
}int main(void)
{int grid[][13] = {{0,0,1,0,0,0,0,1,0,0,0,0,0},{0,0,0,0,0,0,0,1,1,1,0,0,0},{0,1,1,0,1,0,0,0,0,0,0,0,0},{0,1,0,0,1,1,0,0,1,0,1,0,0},{0,1,0,0,1,1,0,0,1,1,1,0,0},{0,0,0,0,0,0,0,0,0,0,1,0,0},{0,0,0,0,0,0,0,1,1,1,0,0,0},{0,0,0,0,0,0,0,1,1,0,0,0,0}};int gridColSize =13;int **p = malloc(sizeof(int)*8);for(int i=0;i<8;i++){p[i]=grid[i];}int max = maxAreaOfIsland(p,8,&gridColSize);printf("max=%d\n",max);return 0;}

求島嶼最大面積，也就是從一個結點出發，我們按前后左右方向走，可以走的最大格子數（可達最大區域）。

我們訪問過一個位置后，使用深度優先遍歷的話，我們可以有四個選擇，也就是水平或者豎直的四個方向上，這對應深度優先遍歷，就是每個結點都有四個子樹。
對于可以訪問的結點，訪問過后，我們將其值1置為0，表示已經訪問過了（0在這個題目當中不需要訪問）。
對于棧，這題我們用遞歸，因為有四個選擇，我們在遞歸時，需要加上四個dfs函數。
結果：
在這里插入圖片描述

回溯法

Backtracking（回溯）屬于 DFS。

普通 DFS 主要用在可達性問題，這種問題只需要執行到特點的位置然后返回即可。
而 Backtracking 主要用于求解排列組合問題，例如有 { ‘a’,‘b’,‘c’ } 三個字符，求解所有由這三個字符排列得到的字符串，這種問題在執行到特定的位置返回之后還會繼續執行求解過程。

因為 Backtracking 不是立即返回，而要繼續求解，因此在程序實現時，需要注意對元素的標記問題：

在訪問一個新元素進入新的遞歸調用時，需要將新元素標記為已經訪問，這樣才能在繼續遞歸調用時不用重復訪問該元素；
但是在遞歸返回時，需要將元素標記為未訪問，因為只需要保證在一個遞歸鏈中不同時訪問一個元素，可以訪問已經訪問過但是不在當前遞歸鏈中的元素。

def backtrack(路徑, 選擇列表):if 滿足結束條件:result.add(路徑)returnfor 選擇 in 選擇列表:做選擇backtrack(路徑, 選擇列表)撤銷選擇以上三種定義：
1、路徑：也就是已經做出的選擇
2、選擇列表：也就是當前可以做的選擇
3、結束條件：也就是到達決策樹底層，無法再做選擇的條件

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <math.h>
/*** 本解答模仿 https://www.cnblogs.com/wuyuegb2312/p/3273337.html 編寫* 本解答以供自己學習提升和分享 MasterXU*/
static char g_ch[10][4] = {"","","abc","def","ghi","jkl","mno","pqrs","tuv","wxyz",
};
static int g_total[10] ={0,0,3,3,3,3,3,4,3,4}; 
/*** number: 輸入待轉換數字* answer：解空間,存放路徑上每個節點的選擇,由于是遞歸實現 需要保存1條路徑節點即可* index:  當前深度* depth:  最大路徑深度* ans:    返回結果* pathIdx:當前路徑編號*/
void recursive(char *number, int *answer, int index, int depth, char **ans, int *pathIdx)
{//當當前深度等于最大深度時，表示此時DFS遍歷完一條路徑了，需要將這條路徑的元素記錄if(index == depth){//分配存放該路徑上元素的內存ans[*pathIdx] = (char *)malloc((depth+1)*sizeof(char));//獲取該路徑每層的元素，number[i]-'0'表示選的層數，answer[1]表示選該層的元素for(int i=0;i<depth;i++){ans[*pathIdx][i]=g_ch[number[i]-'0'][answer[i]];}ans[*pathIdx][depth]='\0';//下一次記錄下一路徑的元素(*pathIdx)++;//返回表示該路徑已經記錄完畢return;}/*index+1：表示遍歷下一層answer[index+1]++：遍歷下一個兄弟結點 */for(answer[index]=0;answer[index]<g_total[number[index]-'0'];answer[index]++){recursive(number,answer,index+1,depth,ans,pathIdx);}
}/*** Note: The returned array must be malloced, assume caller calls free().*/
char ** letterCombinations(char * digits, int* returnSize){int a[100] = {0};   //記錄深度遍歷每條路徑上結點的位置int depth = strlen(digits); //深度優先遍歷的最大深度int num = (int)pow(4,depth);    //深度優先遍歷的最多路徑個數*returnSize = 0;    //路徑計數if(depth == 0)return NULL;char **ans = (char **)malloc(num*sizeof(char *));recursive(digits,a,0,depth,ans,returnSize);return ans;}int main(void)
{char *digits = "23";int returnSize =0;char **ans = letterCombinations(digits,&returnSize);printf("returnSize = %d\n",returnSize);for(int i =0;i<returnSize;i++){puts(ans[i]);}return 0;
}