排序

1. 冒泡排序

>> 冒泡排序的思想

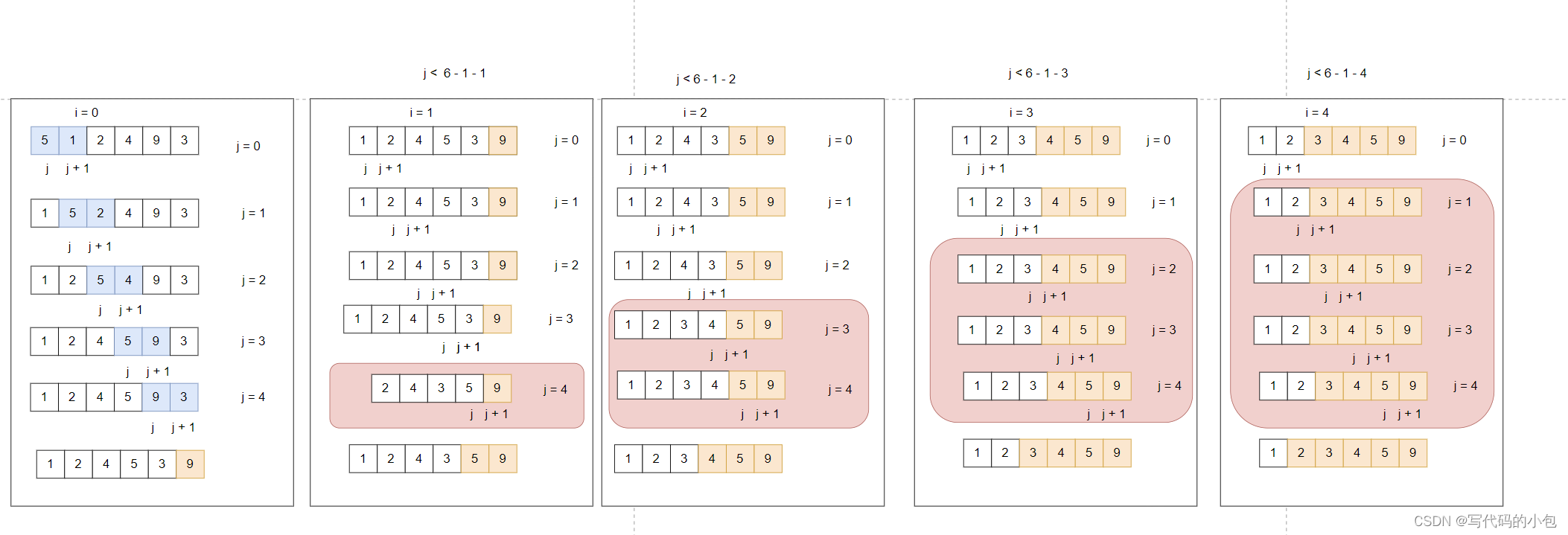
冒泡排序是一種簡單的排序算法，其基本思想是通過多次遍歷待排序序列，依次比較相鄰的元素并交換位置，使得每次遍歷后最大（或最小）的元素冒泡到序列的末尾。具體步驟如下：

1. 從待排序序列的第一個元素開始，依次比較相鄰的兩個元素。
2. 如果前一個元素大于后一個元素，則交換這兩個元素的位置，使得較大的元素向后移動。
3. 繼續比較下一對相鄰元素，重復上述操作，直到遍歷到序列的倒數第二個元素。
4. 重復執行上述操作，每次遍歷使得最大的元素冒泡到序列的末尾。
5. 重復以上步驟，直到所有元素都排序完成。

冒泡排序的時間復雜度為 O(n^2)，其中n為待排序序列的長度。雖然冒泡排序的時間復雜度較高，在處理大規模數據時效率較低，但由于其簡單直觀的思想和實現方式，適用于小規模數據的排序任務。

>> 冒泡排序代碼實現

public class BubbleSorting {public static void main(String[] args) {int[] arr = {46, 28, 69, 39, 4, 23, 76, 84, 78, 81, 18, 91, 27, 52};// 冒泡排序for (int i = 0; i < arr.length - 1; i ++) {for (int j = 0; j < arr.length - 1 - i; j ++) {if (arr[j] > arr[j + 1]) {arr[j] = arr[j] ^ arr[j +1];arr[j+1] = arr[j] ^ arr[j +1];arr[j] = arr[j] ^ arr[j +1];}}}System.out.println(Arrays.toString(arr));}
}
// 輸出：[4, 18, 23, 27, 28, 39, 46, 52, 69, 76, 78, 81, 84, 91]

2. 選擇排序

>> 選擇排序的思想

選擇排序的思想是通過不斷地選擇未排序序列中的最小（或最大）元素，并將其放到已排序序列的末尾，逐步構建有序序列。具體步驟如下：

1. 首先，將待排序序列分為兩部分：已排序序列和未排序序列。初始時，已排序序列為空，未排序序列包含待排序的所有元素。
2. 在未排序序列中找到最小（或最大）的元素，記為最小值（或最大值）。
3. 將最小值與未排序序列的第一個元素進行交換，將最小值放到已排序序列的末尾。
4. 縮小未排序序列的范圍，將已排序序列增加一個元素，重復步驟2和步驟3，直到未排序序列為空。

通過不斷地選擇未排序序列中的最小（或最大）元素，并將其放到已排序序列的末尾，最終可以得到一個有序序列。

選擇排序的特點是簡單直觀，代碼實現相對較簡單，但效率較低。其時間復雜度為 O(n^2)，其中n是待排序元素的數量。無論待排序序列的初始順序如何，選擇排序的比較次數和交換次數都是固定的，因此它的時間復雜度相對穩定。然而，由于每次都要進行交換操作，選擇排序在大規模數據的排序過程中效率較低，一般不適用于大規模或需要高效排序的場景。

>> 選擇排序代碼實現

public class SelectSort2 {public static void main(String[] args) {int[] arr = {46, 28, 69, 39, 4, 23, 76, 84, 78, 81, 18, 91, 27, 52};// 選擇排序for (int i = 0; i < arr.length-1; i++) {int min = i;for (int j = i + 1; j < arr.length; j++) {if (arr[min] > arr[j]) {min = j;}}int temp = arr[i];arr[i] = arr[min];arr[min] = temp;}System.out.println(Arrays.toString(arr));}
}
// 輸出：[4, 18, 23, 27, 28, 39, 46, 52, 69, 76, 78, 81, 84, 91]

3. 插入排序

>> 插入排序的思想

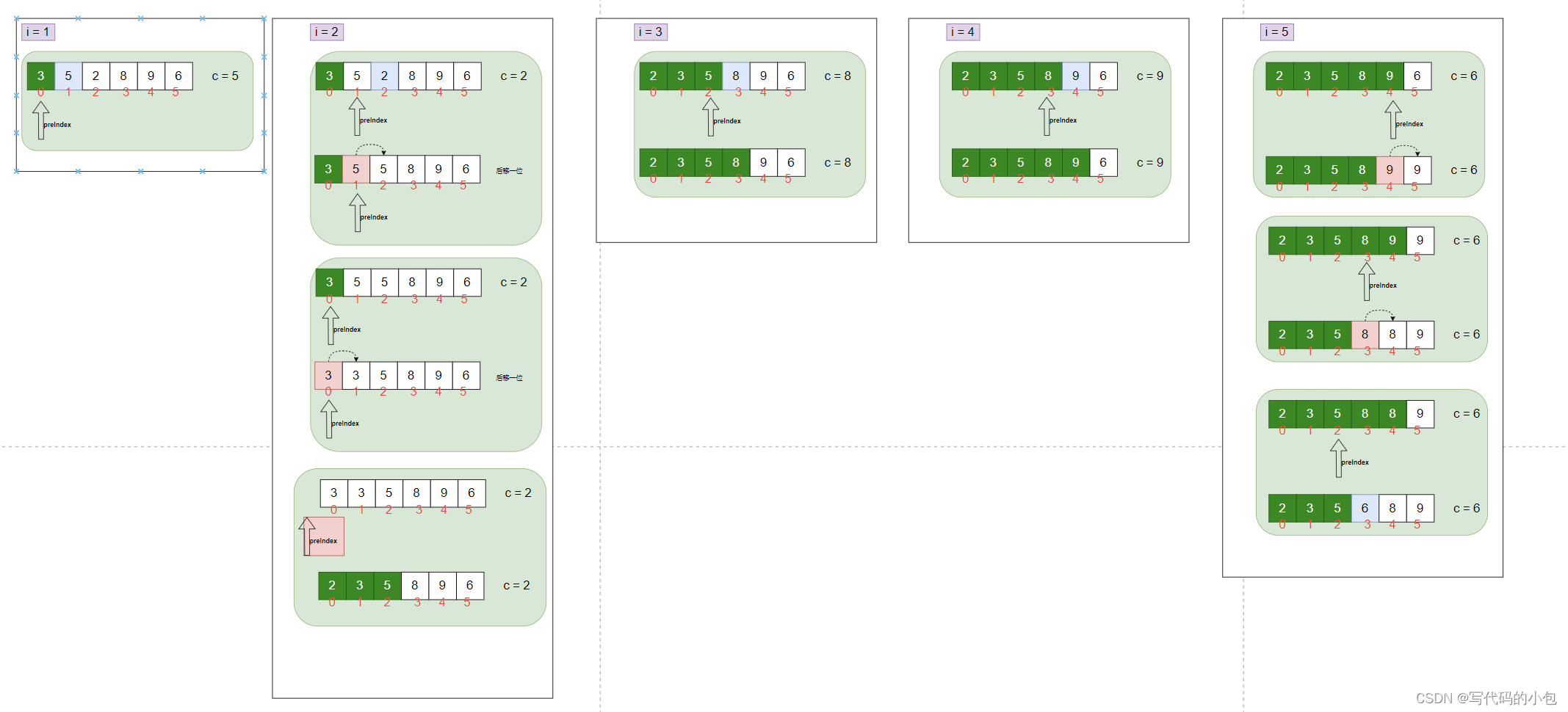
插入排序的思想是將待排序的元素逐個插入到已排序序列中的正確位置，從而逐步構建有序序列。具體步驟如下：

1. 首先，將待排序序列分為兩部分：已排序序列和未排序序列。初始時，已排序序列只包含第一個元素，未排序序列包含剩余的元素。
2. 從未排序序列中取出第一個元素，將其視為當前元素。
3. 將當前元素與已排序序列從右往左進行比較，找到合適的位置插入。
4. 將當前元素插入到已排序序列中的正確位置，同時調整已排序序列的元素位置，使其仍然保持有序。
5. 重復步驟2至步驟4，直到未排序序列中的所有元素都被插入到已排序序列中。

通過不斷地將待排序序列中的元素插入到已排序序列的正確位置，最終可以得到一個有序序列。

插入排序的特點是相對于其他簡單排序算法（如選擇排序、冒泡排序），效率要高一些。其時間復雜度為O(n^2)，其中n是待排序元素的數量。插入排序在對近乎有序的數據進行排序時，效果較好，而在對大規模亂序數據進行排序時，效率相對較低。盡管如此，插入排序的實現簡單，對于小規模或部分有序的數據集合，仍然是一種有效的排序方法。

>> 插入排序代碼實現

public class InsertSort {public static void main(String[] args) {int[] arr = {46, 28, 69, 39, 4, 23, 76, 84, 78, 81, 18, 91, 27, 52};for (int i = 1; i < arr.length; i++) {int index = i - 1;int num = arr[i];while (index >= 0 && num < arr[index]) {arr[index + 1] = arr[index];index --;}arr[index + 1] = num;}System.out.println(Arrays.toString(arr));}
}

4. 二分法查找

>> 二分法查找的思想

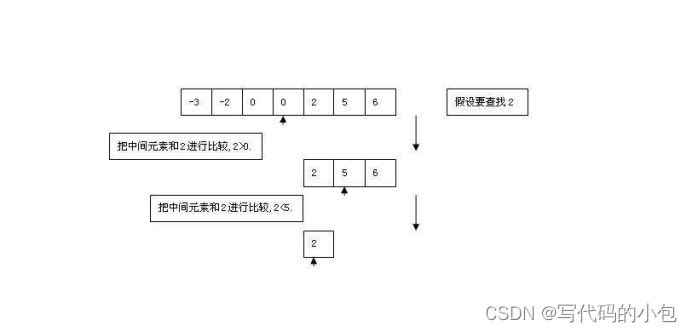
二分法查找是一種高效的查找算法，適用于已排序的數組。其基本思想是將待查找區間不斷二分，通過比較目標值與中間元素的大小關系來確定下一步查找的范圍。具體步驟如下：

1. 確定查找區間的起始和結束位置，通常為整個數組的起始和結束位置。
2. 計算查找區間的中間位置 mid，可以取 (start + end) / 2。
3. 比較目標值與中間元素的大小關系：
4. 如果目標值等于中間元素，那么就找到了目標值，返回索引。
5. 如果目標值小于中間元素，說明目標值可能在左半部分，更新結束位置為 mid - 1。
6. 如果目標值大于中間元素，說明目標值可能在右半部分，更新起始位置為 mid + 1。
7. 重復步驟 2 和步驟 3，直到目標值找到或者查找區間為空（起始位置大于結束位置）為止。

二分法查找的時間復雜度為 O(log n)，其中 n 是待查找區間內元素的個數。這使得它成為處理大規模數據的一種高效算法。

需要注意的是，二分法查找要求待查找的數組必須是有序的，否則查找結果將不可靠。另外，如果數組中存在重復元素，二分查找可能無法找到第一個或最后一個目標值的索引，需要進行額外的處理。

>> 二分法查找代碼實現

public class BinarySearch {public static void main(String[] args) {int[] arr = {1,2,3,4,5,6};int key = 2;int index = binarySearch(arr, key);System.out.println(arr[index]);}// 二分法查找static int binarySearch(int[] arr, int key) {int left = 0, right = arr.length - 1;while (left <= right) {int mid = (left + right) >> 1;if (arr[mid] > key) {right = mid - 1;} else if (arr[mid] < key) {left = mid +1;} else {return mid;}}return -1;}
}