代碼參考《妙趣橫生的算法.C語言實現》
文章目錄
- 前言
- 1、圖的概念
- 2、圖的存儲形式
- 1、鄰接矩陣:
- 2、鄰接表
- 3、代碼定義鄰接表
- 3、圖的創建
- 4、深度優先搜索DFS
- 5、廣度優先搜索BFS
- 6、實例分析
前言
本章總結:圖的概念、圖的存儲形式、鄰接表定義、圖的創建、圖的遍歷(DFS、BFS)、
以及最后給出一個實例分析
1、圖的概念
圖是由頂點的非空有限集合V與邊的集合E(頂點之間的關系)所構成。
圖分為有向圖和無向圖。
2、圖的存儲形式
最常見的兩種:鄰接矩陣、鄰接表
1、鄰接矩陣:
利用兩個數組來存儲一個圖。
第一個數組為一維數組,用來存放圖中的數據。vertex[0,1,…,n-1]:存儲頂點信息
第二個數組為二維數組,用來存儲頂點的相互關系,稱為鄰接矩陣。
A[i][j]={1,當頂點i與頂點j之間有邊 0,當頂點i與頂點j之間沒有邊}
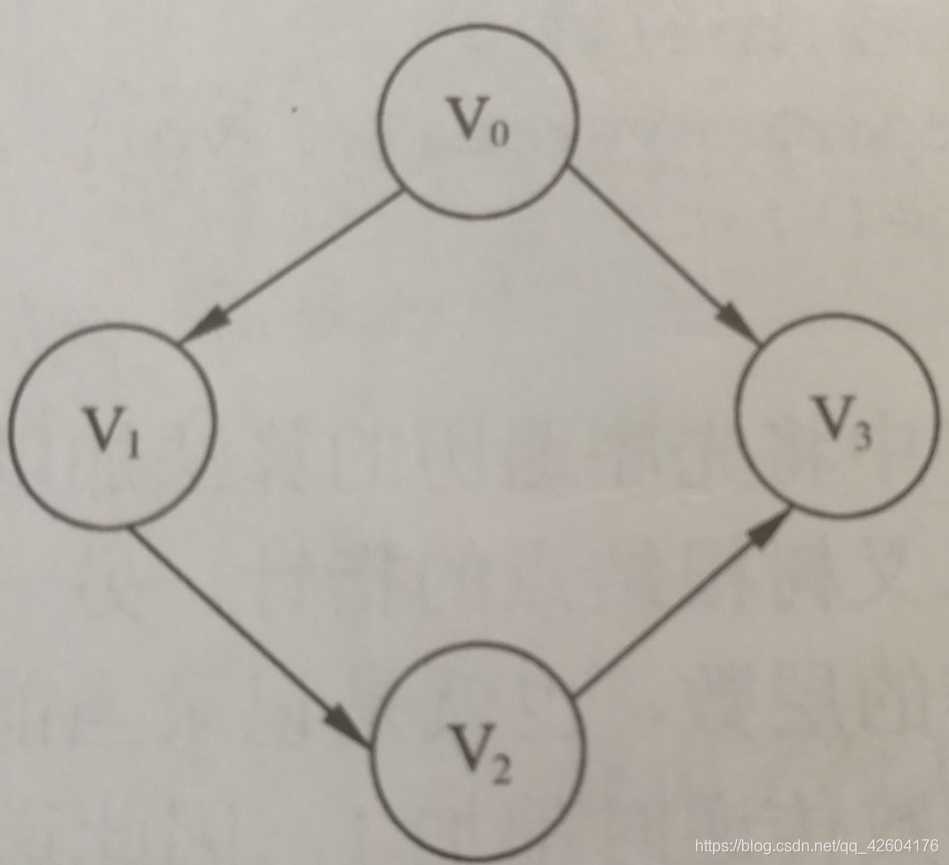 有向圖 有向圖 | 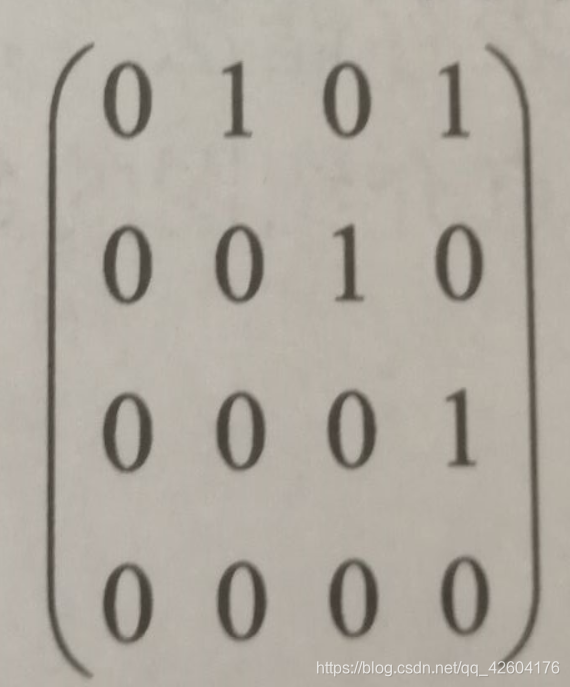 有向圖的鄰接矩陣 有向圖的鄰接矩陣 |
通過簡單的鄰接矩陣就可以把一個復雜的圖關系表現出來,不過該方法不適合存儲稀疏圖(邊數目少的圖)
2、鄰接表
鄰接表由鏈表和順序數組組成。鏈表用來存放邊的信息,數組用來存放頂點的數據信息。
每一個頂點分別建立一個鏈表。
每個鏈表前面設置一個頭結點,頂點域vertex用來存放頂點數據信息,指針域next指向依附于頂點vertex的第一條邊。
| vertex | next |
|---|
每一個鏈表中,鏈表的每一個結點陳偉邊結點,表示依附于對應頂點的一條邊。adjvex域存放該邊的另一端頂點在頂點數組中的位置(數組下標);weight存放邊的權重;next指向下一條邊結點,若是最后一個邊結點,則指向NULL;
| adjvex | weight | next |
|---|
分別對應了頭結點以及邊結點:
 有向圖 有向圖 | 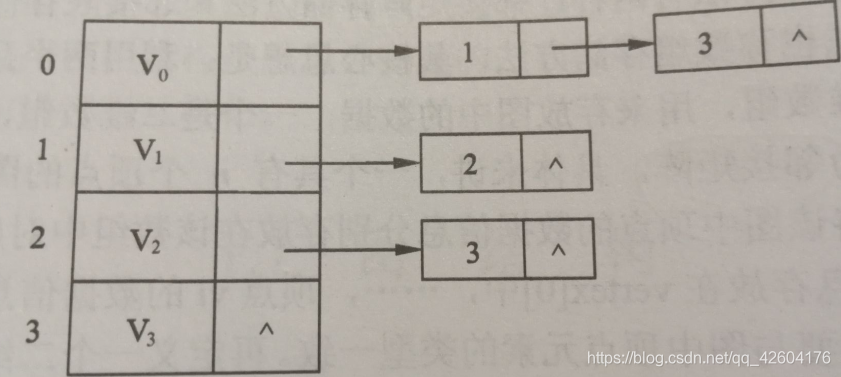 有向圖的鄰接表 有向圖的鄰接表 |
3、代碼定義鄰接表
//鄰接表定義
#define MAX_VERTEX_NUM 20 //指定圖中頂點最大的個數為20
typedef struct ArcNode
{//單鏈表中結點類型int adjvex; //該邊指向頂點在順序表中的位置(數組下標)struct ArcNode *next; //指向下一條邊的指針infoType *weight; //邊上的權重
}ArcNode;typedef struct VNode
{//頂點類型VertexType data; //頂點中的數據信息,為VertexType類型ArcNode *firstarc; //指向單鏈表,即指向一條邊
}VNode;VNode G[MAX_VERTEX_NUM]; //VNode類型的數組G,它是圖中頂點的存儲容器。
3、圖的創建
圖的創建就是創建一個基于鄰接表存儲的圖結構。在此之前,必須先設計好圖的邏輯結構。
步驟:
1、創建圖的頂點,也就是創建存儲圖中頂點的順序表
2、創建頂點之間的邊,也就是創建單鏈表。
代碼描述如下:
1、首先向頂點中賦值。通過Getdata得到每個頂點中的數據,并將它賦值到G[i].data中去。
每個頂點的firstarc域要初始化為NULL
2、然后創建頂點之間的邊。創建時應該嚴格按照最開始所設計的圖的邏輯結構進行邊的輸入。
創建邊的過程與創建鏈表的過程類似。
當輸入-1時,表示該頂點依附的邊創建完成
//圖的創建
GreatGraph(int n,VNode G[])
{int i,e;ArcNode *p,*q;printf("輸入頂點信息\n");for(i=0;i<n;i++){ Getdata(G[i]); //得到每條頂點中的數據 G[i].firstarc=NULL; //初始化每一個頂點第一條邊為空}for(i=0;i<n;i++){printf("創建第%d個頂點的邊");scanf("%d",&e); //輸入邊指向的頂點坐標while(e!=-1){p=(ArcNode *)malloc(sizeof(ArcNode)); //創建一條邊p->next =NULL; //鏈表結點next指向空p->adjvex = e; //將該邊指向頂點的信息賦值給adjvexif(G[i].firstarc == NULL)G[i].firstarc=p; //i結點的第一條邊else q->next = p;q=p;scanf("%d",&e);}}
}//如果是創建上面提到過的有向圖,則:
void main()
{VNode G[3];CreatGpraph(3,G);
}
4、深度優先搜索DFS
圖的遍歷:從圖的某一頂點出發,訪遍圖中其余頂點,且使每個頂點只被訪問一次。
圖的遍歷可用于 求解圖的連通性問題,拓撲排序,求解最短路徑,求解關鍵路徑
深度優先搜索的基本思路:
從圖中的某個頂點v出發,訪問該頂點v,然后再一次從v的未被訪問過的鄰接點出發,繼續優先深度優先遍歷該圖,直到圖中與頂點v路徑相通的頂點都被訪問到為止。
由于一個圖結構未必是連通的,因此一次的深度優先搜索不一定可以遍歷到圖中所有的頂點,若此時圖中仍然有頂點未被訪問,
就另選圖中的一個沒有被訪問到的頂點作為起始點,繼續深度優先搜索。
重復上述操作,直到圖中所有頂點都被訪問到為止。
深度優先搜索是一個遞歸操作,重復“訪問頂點v,再依次從v未被訪問過的鄰接點出發繼續深度優先搜索”
//代碼描述
/*
深度優先搜索一個連通圖
*/
void DFS(VNode G[],int v)
{int w;visit(v); //訪問當前頂點visited[v] =1; //將頂點v對應的訪問標記置1w=FirstAdj(G,v); //找到頂點v的第一個鄰接點,如果無鄰接點返回-1while(w!=-1){if(visited[w]==0) //如果該頂點未被訪問{DFS(G,w); //遞歸地進行深度優先訪問w=NextAdj(G,v); //找到頂點v的下一個鄰接點,如果沒有返回-1}}
}//對圖中G=(V,E)進行深度優先搜索的主算法
void Travel_DFS(VNode G[],int visited[],int n)
{int i;for(i=0;i<n;i++)visited[i]=0; //將標記數組初始化為0for(i=0;i<n;i++)if(visited[i]==0) //若有頂點未被訪問,從該頂點開始繼續深度優先搜索DFS(G,i);
}
Travel_DFS 函數包含了3個參數
G[]表示存儲圖結構的容器,這里可以理解為鄰接表
visited[]為設置的方位標志數組,用來標記圖中被訪問過的頂點
n表示圖中的頂點個數。
將visited初始化為0,因為一開始時,圖中的任何定點都沒有被訪問。
然后從第一個沒有被訪問的頂點開始調用遞歸函數DFS,從該頂點開始深度優先遍歷整個圖
之所以不能僅僅通過一個遞歸函數DFS()來遍歷整個圖,是因為DFS只能遍歷到從起始頂點v開始所有與v相連通的圖的頂點。
如果這個圖不是連通的,僅僅通過DFS是無法遍歷完全的
可以舉個例子來描述詳細遍歷過程:

假設以V0為起點,訪問標志數組初始值為visited[5]={0,0,0,0,0};
{(1)訪問頂點V0,visited[5]=1,0,0,0,0(2)用函數FirstAdj得到V0第一個鄰接點,如V1(3)如果不返回-1,即有鄰接點(3.1)訪問頂點V1,visited[5]=1,1,0,0,0(3.2)用函數FirstAdj得到V1第一個鄰接點,V2(因為V0已經訪問過了)(3.3)如果不返回-1,即有鄰接點(3.3.1)訪問頂點V2,visited[5]=1,1,1,0,0(3.3.2)用函數FirstAdj得到V2第一個鄰接點,返回-1,因為都被訪問過了(3.4)用函數NextAdj()得到V1下一個鄰接點返回-1,因為都被訪問過兒(4)用函數NextAdj()得到V0下一個鄰接點返回-1,因為都被訪問過兒\begin{cases} (1)& \text{訪問頂點V0,visited[5]={1,0,0,0,0}}\\ (2)& \text{用函數FirstAdj得到V0第一個鄰接點,如V1}\\ (3)& \text{如果不返回-1,即有鄰接點}\\ (3.1)& \text{訪問頂點V1,visited[5]={1,1,0,0,0}}\\ (3.2)& \text{用函數FirstAdj得到V1第一個鄰接點,V2(因為V0已經訪問過了)}\\ (3.3)& \text{如果不返回-1,即有鄰接點}\\ (3.3.1)& \text{訪問頂點V2,visited[5]={1,1,1,0,0}}\\ (3.3.2)& \text{用函數FirstAdj得到V2第一個鄰接點,返回-1,因為都被訪問過了}\\ (3.4)& \text{用函數NextAdj()得到V1下一個鄰接點返回-1,因為都被訪問過兒}\\ (4)& \text{用函數NextAdj()得到V0下一個鄰接點返回-1,因為都被訪問過兒}\\ \end{cases}????????????????????????????????????????(1)(2)(3)(3.1)(3.2)(3.3)(3.3.1)(3.3.2)(3.4)(4)?訪問頂點V0,visited[5]=1,0,0,0,0用函數FirstAdj得到V0第一個鄰接點,如V1如果不返回-1,即有鄰接點訪問頂點V1,visited[5]=1,1,0,0,0用函數FirstAdj得到V1第一個鄰接點,V2(因為V0已經訪問過了)如果不返回-1,即有鄰接點訪問頂點V2,visited[5]=1,1,1,0,0用函數FirstAdj得到V2第一個鄰接點,返回-1,因為都被訪問過了用函數NextAdj()得到V1下一個鄰接點返回-1,因為都被訪問過兒用函數NextAdj()得到V0下一個鄰接點返回-1,因為都被訪問過兒?
5、廣度優先搜索BFS
廣度優先搜索基本思路:
從圖中的指定頂點v出發,先訪問頂點v,然后依次訪問v的各個未被訪問的鄰接點,然后從這些鄰接點出發,按照同樣的原則依次訪問它們未被訪問的鄰接點
如此循環,直道圖中所有與v相連通的鄰接點都被訪問。
若此時圖中仍有頂點未被訪問,就另選圖中的一個沒有被訪問到的頂點作為起始點,繼續廣度優先搜索,直道圖中所有頂點都訪問完為止。
深度優先特點:從一個頂點深入下去,深入到不能再深入下去為止,再從另一個未被訪問過的頂點深入下去。
廣度優先特點:按層次遍歷的方法,即先訪問離頂點v0最近的頂點v1,v2,v3,…再逐一訪問離v1 v2 v3 …最近的頂點
算法思路:
【A】
1、訪問頂點v
2、每訪問到一個頂點。都將對應的訪問標簽置1
3、將一杯訪問過的頂點v入隊列
【B】
循環執行以下操作:
1、從隊列中取出隊頭元素(頂點v)
2、得到該頂點的第一個鄰接點
3、如果該鄰接點還沒被訪問、則訪問,并入隊列,訪問標記置1
4、求頂點v的下一個鄰接點,如果存在鄰接點,則跳回步驟3,如果不存在鄰接點,跳回到步驟1
循環執行上述操作,直到隊列取空為止。
一旦隊列取空則表明最后訪問到的頂點已經沒有未訪問到的鄰接點了
代碼描述:
void BFS(VNode G[],int v)
{int w;visit(v); //訪問頂點vvisited[v]=1; //將頂點v對應的訪問標記置1EnQueue(q,v); //頂點v入隊列while(!emptyQ(q)){DeQueue(&q,&v); //出隊列,元素由v返回w = FirstAdj(G,v); //找到頂點v的第一個鄰接點,如果無鄰接點返回-1while(w!=-1){if(visited[w]==0){visit(w);EnQueue(q,w); //頂點w入隊列visited[w]=1;}w=NextAdj(G,v); //找到頂點v的下一個鄰接點,如果無鄰接點,返回-1}}
}//對圖G=(V,E)進行廣度優先搜索的主要算法
void Travel_BFS(VNode G[],int visited[],int n)
{int i;for(i=0;i<n;i++){visited[0]=0; //標記數組初始化為0}for(i=0;i<n;i++){if(visited[i]==0) //如果頂點未被訪問到,從該頂點開始繼續廣度優先搜索BFS(G,i);}
}
/*
BFS實現廣度優先搜索一個連通的圖,參數G[]表示圖的存儲容器,即鄰接表
v表示廣度優先遍歷訪問起點
可以舉個例子來描述詳細遍歷過程:

1、visit(V0),visited[5]={1,0,0,0,0} queue: V0
2、QueOut(V0),Firstadj(V0)=V1,visit(V1) queue:
3、visit(V1),visited[5]={1,1,0,0,0} queue: V1
4、NextAdj(V0)=V2,visit(V2) queue: V1
5、visit(V2),visited[5]={1,1,1,0,0} queue: V1,V2
6、NextAdj(V0)=-1 queue: V1,V2
7、QueOut(V1),Firstadj(V1)=V3,visit(V3) queue: V2
8、visit(V3),visited[5]={1,1,1,1,0} queue: V2,V3
9、NextAdj(V1)=V4,visit(V4) queue: V2,V3
10、visit(V4),visited[5]={1,1,1,1,1} queue: V2,V3,V4
11、NextAdj(V1)=-1 queue: V2,V3,V4
12、QueOut(V2),Firstadj(V2)=-1 queue: V3,V4
14、QueOut(V3),Firstadj(V3)=-1 queue:V4
15、QueOut(V4),Firstadj(V4)=-1 queue:
此數據結構為二叉樹結構,所以廣度優先搜索適用于對樹結構的遍歷,因為樹結構是標準的層次結構
注意,我們這里的遍歷是按照圖中每個頂點之間的關系對一個圖的各連通分量進行的遍歷,而不只是對圖中的每個頂點進行訪問那么簡單。圖的遍歷可能帶有其他操作如:計算帶權有向圖邊權之和,記錄有向圖頂點訪問軌跡,記錄兩頂點之間的邊權值問題,都必須依賴圖的遍歷。
6、實例分析
這里實例化上面涉及到的兩個函數FirstAdj()和NextAdj();
FirstAdj():
功能:返回頂點的第一個鄰接點在數組G的下標,如果該頂點無鄰接點,返回-1
//返回第一個鄰接點在數組中的下標
int FirstAdj(VNode G[],int v)
{if(G[v].firstarc!=NULL) return (G[v].firstarc)->adjvex; //如過該結點有第一條邊,返回下標,否則返回-1return -1;
}NextAdj():
功能:返回頂點的下一個鄰接點在數組G的下標,如果該頂點無鄰接點,或者該點所有鄰接點都被訪問過,返回-1
//返回下一個鄰接點在數組中的下標
int NextAdj(VNode G[],int v)
{ArcNode *p;p=G[v].firstarc;while(p!=NULL){if(visited[p->adjvex]) p=p->next; //如果已經訪問過,返回-1else return p->adjvex;}return -1;
}
用鄰接表存儲的形式創建一棵無向圖,并應用深度優先搜索方法遍歷該圖中的每個頂點
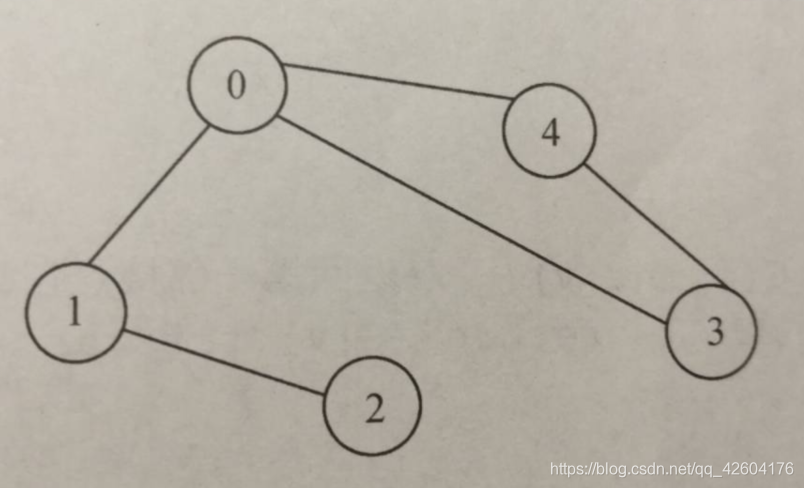
#include <stdio.h>
#include <stdlib.h>
#include "malloc.h"
#include "conio.h"//鄰接表定義
#define MAX_VERTEX_NUM 20 //指定圖中頂點最大的個數為20
typedef int VertexType ;
typedef struct ArcNode
{//單鏈表中結點類型int adjvex; //該邊指向頂點在順序表中的位置(數組下標)struct ArcNode* next; //指向下一條邊的指針//infoType* weight; //邊上的權重
}ArcNode;typedef struct VNode
{//頂點類型VertexType data; //頂點中的數據信息,為VertexType類型ArcNode* firstarc; //指向單鏈表,即指向一條邊
}VNode;VNode G[MAX_VERTEX_NUM]; //VNode類型的數組G,它是圖中頂點的存儲容器。
int visited[5] = { 0,0,0,0,0 };//圖的創建
void GreatGraph(int n, VNode G[])
{int i, e;ArcNode* p, * q;q = NULL;printf("輸入頂點信息\n");for (i = 0;i < n;i++){scanf("%d", &G[i].data); //得到每條頂點中的數據 G[i].firstarc = NULL; //初始化每一個頂點第一條邊為空}for (i = 0;i < n;i++){printf("創建第%d個頂點的邊\n",i);scanf("%d", &e); //輸入邊指向的頂點坐標while (e != -1){p = (ArcNode*)malloc(sizeof(ArcNode)); //創建一條邊p->next = NULL; //鏈表結點next指向空p->adjvex = e; //將該邊指向頂點的信息賦值給adjvexif (G[i].firstarc == NULL)G[i].firstarc = p; //i結點的第一條邊else{q->next = p;}q = p;scanf("%d", &e);}}
}
//返回第一個鄰接點在數組中的下標
int FirstAdj(VNode G[], int v)
{if (G[v].firstarc != NULL) return (G[v].firstarc)->adjvex; //如過該結點有第一條邊,返回下標,否則返回-1return -1;
}//返回下一個鄰接點在數組中的下標
int NextAdj(VNode G[], int v)
{ArcNode* p;p = G[v].firstarc;while (p != NULL){if (visited[p->adjvex]) p = p->next; //如果已經訪問過,返回-1else return p->adjvex;}return -1;
}void DFS(VNode G[], int v)
{int w;printf("%d ", G[v].data); //訪問當前頂點,打印出頂點額數據信息visited[v] = 1; //將頂點v對應的訪問標記置1w = FirstAdj(G, v); //找到頂點v的第一個鄰接點,如果無鄰接點返回-1while (w != -1){if (visited[w] == 0) //如果該頂點未被訪問{DFS(G, w); //遞歸地進行深度優先訪問}w = NextAdj(G, v); //找到頂點v的下一個鄰接點,如果沒有返回-1}
}/*
1、首先向頂點中賦值。通過Getdata得到每個頂點中的數據,并將它賦值到G[i].data中去。
每個頂點的firstarc域要初始化為NULL
2、然后創建頂點之間的邊。創建時應該嚴格按照最開始所設計的圖的邏輯結構進行邊的輸入。
創建邊的過程與創建鏈表的過程類似。
當輸入-1時,表示該頂點依附的邊創建完成
*/
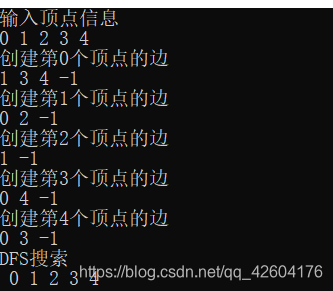
int main()
{VNode G[5];GreatGraph(5, G);printf("DFS搜索\n ");DFS(G, 0);_getche();return 0;
}
效果:
https://blog.csdn.net/ledou2/article/details/81875743
https://blog.csdn.net/ledou2/article/details/81905831





函數以及CSS中的示例)




)
函數以及C ++中的示例)


操作)
)



網絡講解以及tensorflow代碼實現)