On Measuring and Controlling the Spectral Bias of the Deep Image Prior

文章地址：https://arxiv.org/pdf/2107.01125.pdf

代碼地址: https://github.com/shizenglin/Measure-and-Control-Spectral-Bias

參考博客: https://zhuanlan.zhihu.com/p/598650125

---

1. 方法原理

1.1 動機

動機

• Deep Image Prior已經被廣泛地應用于去噪、超分、圖像恢復等
• 但是我們尚不清楚如何在網絡架構的選擇之外控制DIP
• DIP存在性能達到峰值之后退化的問題 --> 需要early stopping

貢獻

• 使用譜偏移度量和解釋 DIP的原理
  • DIP學習目標圖像低頻分量的效率比高頻分量高
• 控制譜偏移
  • 使用Lipschitz-controlled 正則化和 Lipschitz 批歸一化加速和穩定優化過程
  • 使用 上采樣方法（bilinear upsampling）引入了傾向于恢復低頻分量的特點（譜偏移）
  • 使用了一種簡單的early stopping策略防止多余的計算

---

1.2 相關概念

譜偏移原則是指：神經網絡擬合低頻信息的效率比高頻信息快

相關文章參考：

• On the Spectral Bias of Neural Networks
• FREQUENCY PRINCIPLE: FOURIER ANALYSIS SHEDS LIGHT ON DEEP NEURAL NETWORKS

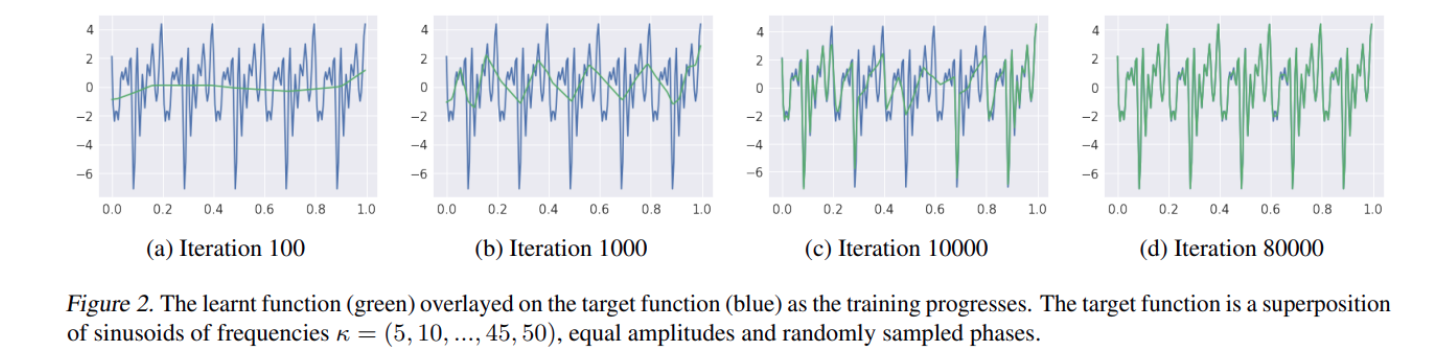
用其中的一些圖進行解釋：

• 隨著迭代的進行，神經網絡的輸出（綠色線）首先擬合的是真實觀測數據的低頻，然后再去逐漸擬合高頻

---

反（逆）問題：根據觀測結果獲取真實模型的一種求解模式。具體的可以參考

• Untrained Neural Network Priors for Inverse Imaging Problems: A Survey

注意反問題求解存在一個普遍的問題：多解性。也就是多個反演結果的合成數據都可以和觀測數據匹配。通常一個減少多解性的方法就是添加約束條件（在公式中表現為正則化約束）

---

1.3 方法原理

頻帶一致度量與網絡退化

??這篇文章是從頻率域的角度進行譜偏移分析的，用 { θ 1 , . . . , θ T } \{\theta^{1},...,\theta^{T}\} {θ1,...,θT}表示第對應迭代次數網絡的參數，用 { f θ 1 , . . . , f θ T } \{f_{\theta^{1}},...,f_{\theta^{T}}\} {fθ1?,...,fθT?}表示對應的網格過程。對圖片頻率分析需要使用傅里葉變換獲得 頻率域的信息，用$F(f_{{\theta }^{(t)}})$表示。頻譜圖的表示如下：

如果對標簽圖片也做一次傅里葉變換，那么可以求解網絡輸出和這個結果的比值
H θ ( t ) = F { f θ ( t ) } F { y 0 } H_{\theta^{(t)}} = \frac{F\{f_{\theta^{(t)}}\}}{F\{y_0\}} Hθ(t)?=F{y0?}F{fθ(t)?}?

• 這個比值越接近于1表示網絡輸出和標簽的相關性越高
• H圖像是一個以中心對稱的圖像，這里為方便統計就將其分割成為多個同心圓環，求圓環中的平均值作為這個圈內的值。也就是將一個二維的度量變為了一個一維的度量。
• 文章中將頻率劃分為了：lowest、low、medium、high和highest五個部分

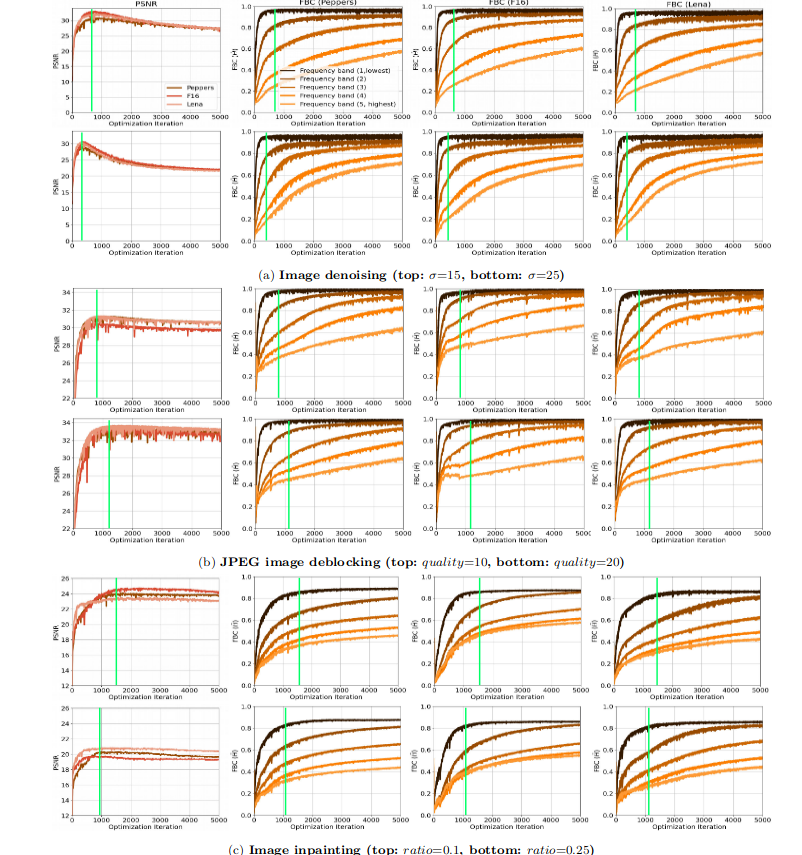
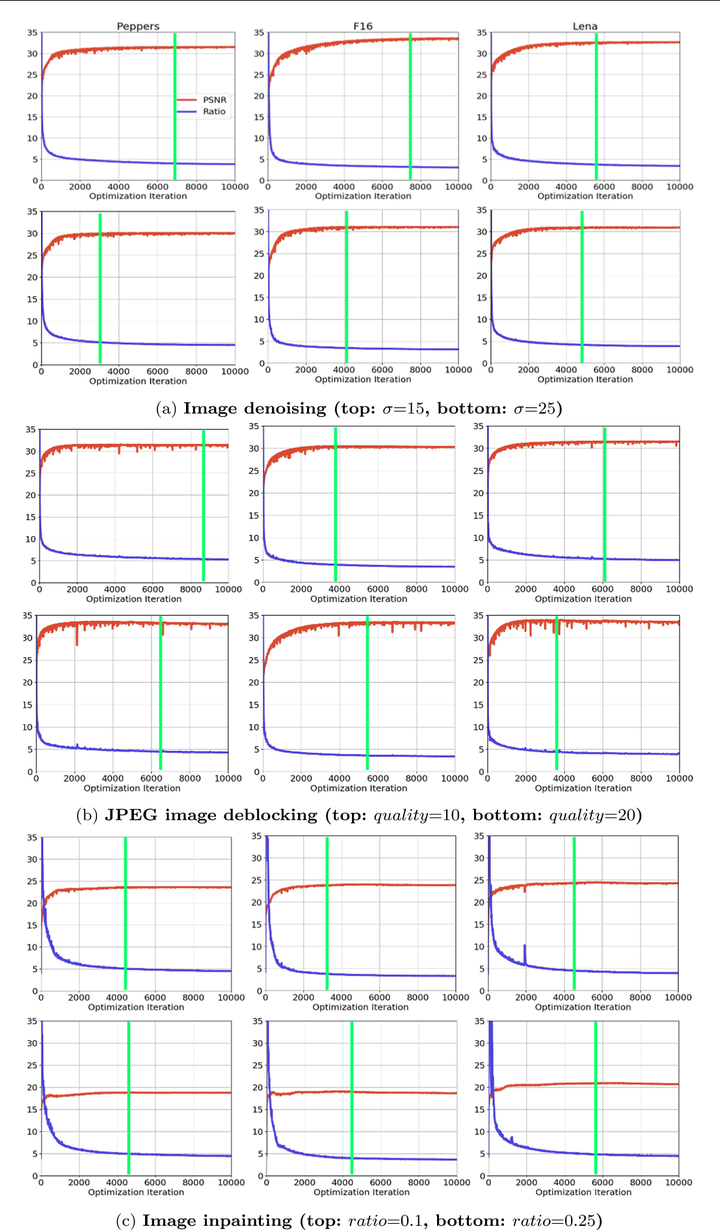
這個度量比值在DIP不同應用場景中隨著迭代次數的變化

• 隨著DIP迭代次數的增加，PSNR會先達到最高然后緩慢降低（性能達到峰值之后會下降）
• 在PSRN最高的時候（圖中綠線），恰好是lowest分量的頻帶一致性剛好最高的時候
• 通過下圖驗證了 DIP也存在譜偏移的現象：低頻分量學得更快且頻帶一致性很高，而高頻分量學習相對較慢且頻帶一致性較低
• 隨著高頻部分的頻帶一致性提高，PSNR下降

---

譜偏移和網絡結構的關系

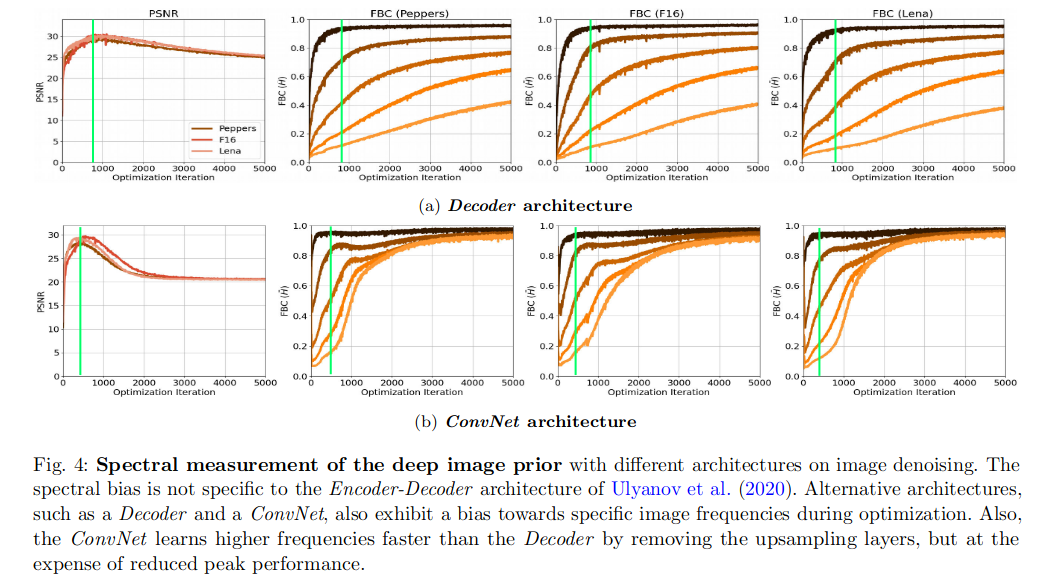
前面有研究表示Encoder-Decoder結構的DIP效果更好，這里作者對比了三種不同結構進行測試對比（a. 沒有Encoder部分的DIP； b. 沒有上采樣層的DIP;）：

• 不論什么結構譜偏移都存在
• 去掉上采樣層的Decoder結構(ConvNet)擬合高頻的效率更高，這里表現為高頻部分的頻帶一致性高
• 無上采樣層的ConvNet結構最大的PSNR比Decoder和DIP低

結論

• 無訓練網絡UNNP可以解決逆圖像問題的原因是：低頻學習效率高，高頻學習效率相對較慢（譜偏移）
• 高頻信息通常為為結構高頻信息和噪聲高頻信息，當網絡開始學習噪聲高頻信息的時候，網絡恢復的性能開始下降
• 這里通過一個類似消融實驗的方法說明上采樣層是可以提高PSNR的，但是這會影響低頻的收斂速度

防止網絡退化，平衡性能與效率的方向

• 保證性能的前提下，使用參數量更少的 Decoder結構 替代DIP的 Encoder-Decoder結構
• 性能退化：抑制網絡對高頻噪聲的學習（使用上采樣層）
• 加速收斂：使用更合適的上采樣層
• 提前停止策略：自動檢測？

---

Lipschitz-controlled 卷積層

從頻率域理解卷積操作

• 對一個時間域/空間域的變量做一個傅里葉變換其實是將作用域變換到了頻率域，這樣的其中一個作用是：
  • 將空間域的卷積操作 變為 頻率域的乘積操作，簡化計算
  • 當然對于信號處理還有更多的好處，比如FK變換可以用于濾波
• 圖像和“卷積核”的作用在頻率域其實就是一個乘積過程
  • 

卷積核具有濾波的作用，但是什么樣的卷積核可以抑制高頻呢？

---

L-Lipschitz連續
這個概念很有意思，WGAN-GP中也用到了

其定義是：如果函數f在區間Q中，以常數L Lipschitz連續，那么對于 $x,y\in Q$有：
$$||f(x)?f(y)||\le L||x?y||$$

常數L就被稱為函數f在區間Q上的 Lipschitz常數。Lipschitz連續其實是限制了連續函數f的局部變動幅度不能超過某一個常量。我個人感覺一個非常更簡單地理解這個概念的方法就是將稍微變動一下這個公式：
$$\frac{||f(x)?f(y)||}{||x?y||}\le L$$
這個東西看起來就像是求導了，更多的可以參考https://blog.csdn.net/FrankieHello/article/details/105739610

---

結合Lipschitz和頻譜分析

假設卷積層的$f$是符合C-Lipschitz的，存在：
$$|\hat{f}(k)|\le \frac{C}{|k{|}^2}\le \frac{||w|{|}_{sn}}{|k{|}^2}$$

• k表示頻率，$|\hat{f}(k)|$表示傅里葉系數的模（有實部和虛部）
• 分母是$k^2$表示在高頻的時候衰減很強，學習更高的頻率需要更高的頻譜范數（分子）
• $||w|{|}_{sn}$ 表示卷積層參數矩陣w的譜范數,可以通過限制譜范數的上限來限制卷積層學習更高頻率的能力
  • $||\frac{w}{||w|{|}_{sn}}|{|}_{sn}=1$, $||\frac{w\lambda }{||w|{|}_{sn}}|{|}_{sn}=\lambda$
  • $\frac{w}{max(1,||w|{|}_{sn}/\lambda )}$

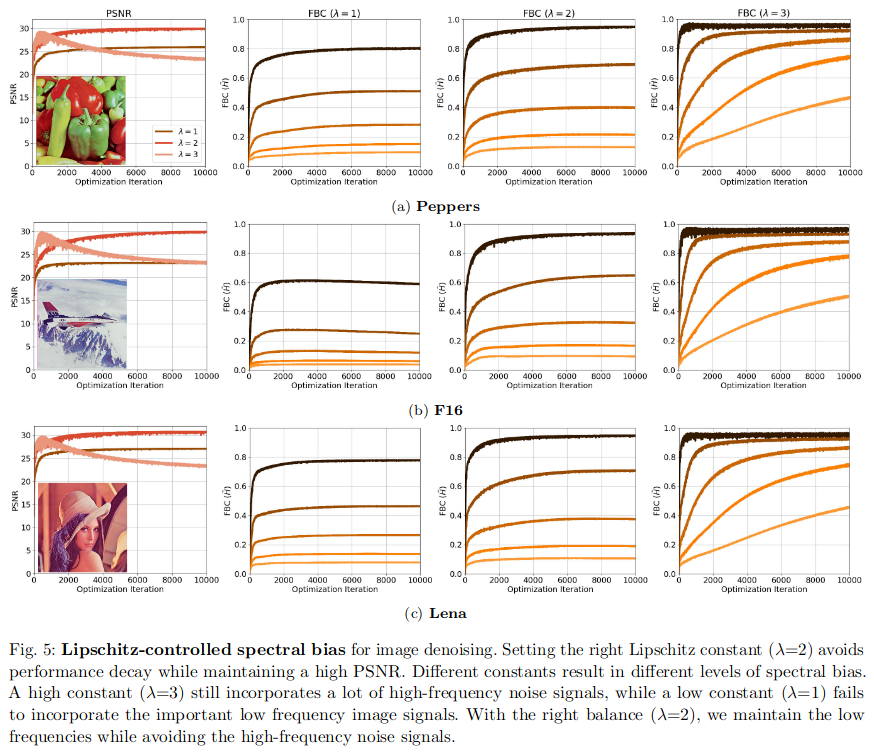
注意這里我們想要達到的一個效果就是：限制最高可以學習的頻率。可以選擇一個合適的$\lambda$在保證恢復效果的同時不去恢復噪聲信號。

其他網絡層對Lipschitz常數的影響

---

Gaussian-controlled 上采樣層

插值、鄰近上采樣層的平滑操作會讓DIP網絡收斂速度變慢，但是上采樣層對于抑制高頻信息又有一定的作用，為了平衡二者作者引入了 gaussian-controlled上采樣層。

方法就是：轉置卷積 + 高斯核

• 轉置卷積可以自定義上采樣的卷積核

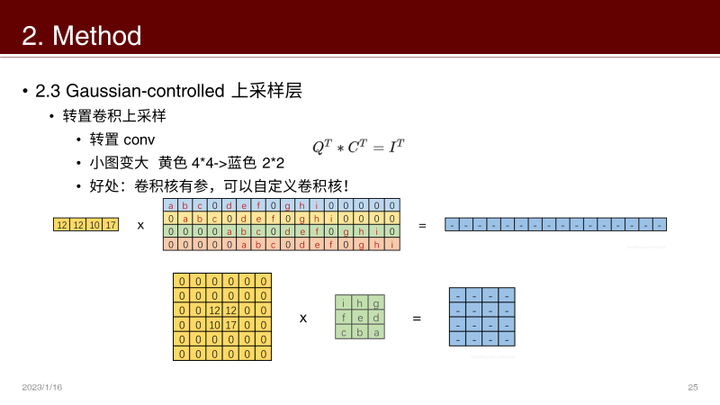
• 為了控制平滑程度，卷積核最簡單的就是高斯核

• 實驗不同的高斯核：$\sigma$越小收斂越快，但是PSNR越小

自動停止迭代過程

• 利用Lipschitz方法限制了網絡學習的最高頻率噪聲，避免了網絡的退化
• 當高頻部分到達了上界限，也就意味著網絡在之前就已經收斂了
• 怎么評估高頻到達了上界限
  • $$r=\frac{Blurriness}{Sharpness}$$
  • 即當模糊度/銳度之間的導數小于預先設置的閾值的時候，停止迭代
  • $$r(f_{\theta })=B(f_{\theta })/S(f_{\theta })$$
  • $$\Delta r(f_{{\theta }^{(t)}})=|\frac{1}{n}\sum _{i=1}^{n}r(f_{\theta }^{(t?n?i)})?\frac{1}{n}\sum _{i=1}^{n}r(f_{\theta }^{(t?n?i)})|$$

2. 實驗結果

• 去噪

  • 

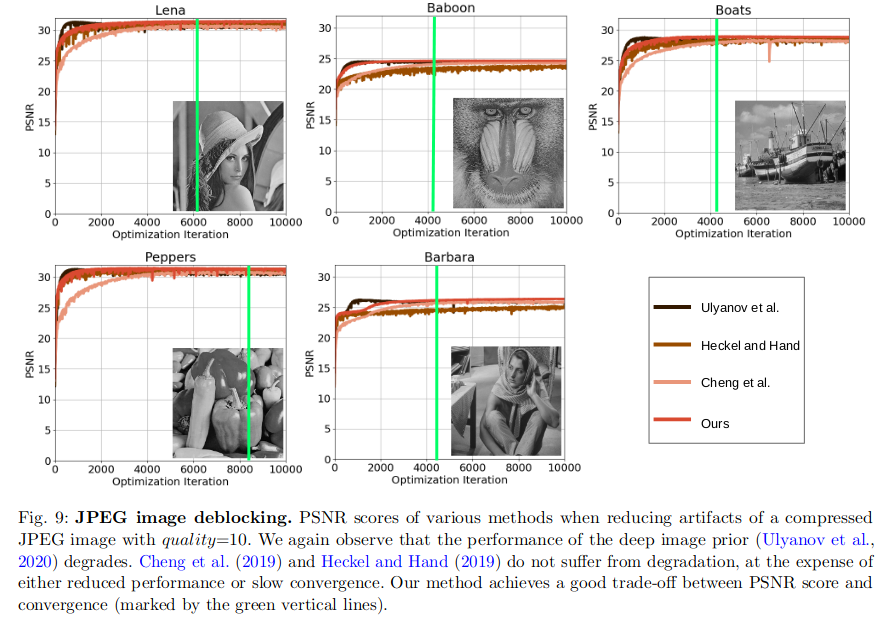
• Image deblockign

  • 

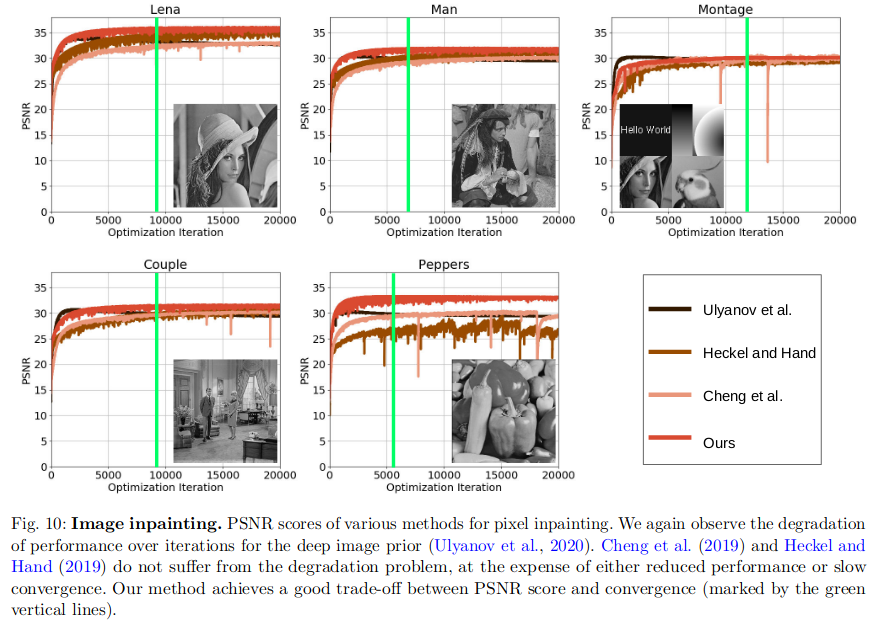
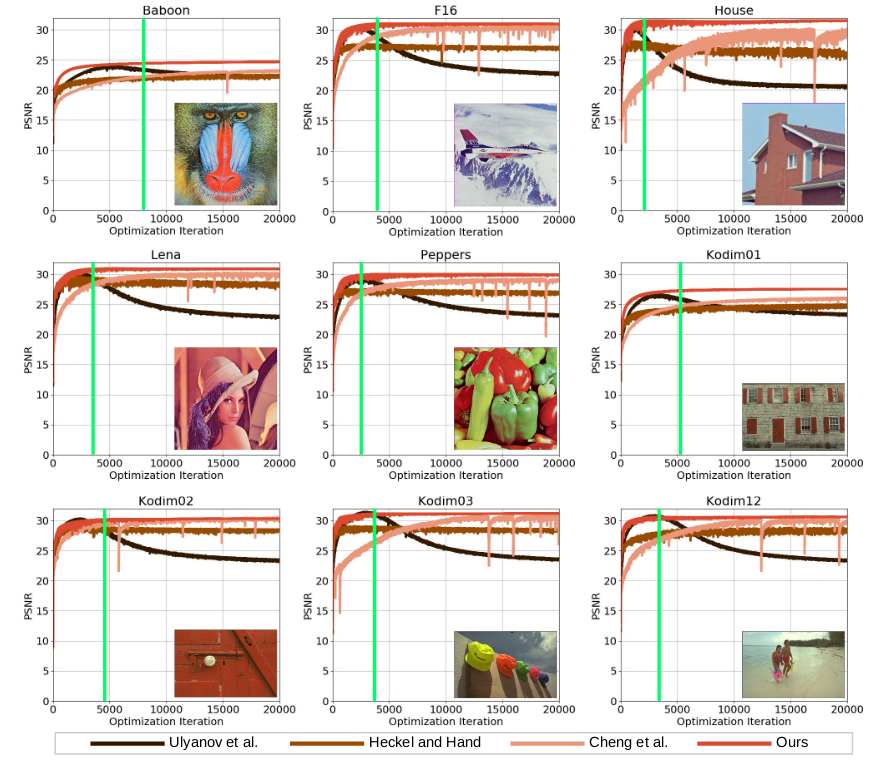
• Image Inpainting

• 

3. 總結

研究思路

1. 從譜偏置方向分析DIP的工作，網絡先擬合低頻信息，逐漸擬合高頻信息
2. 怎么控制擬合高頻信息？–> 高頻截斷 --> 應用Lipschitz理論控制，解決網絡層退化的問題
3. 網絡訓練慢怎么解決？–>分析發現常規的上采樣層相當于一個低通濾波器，引入了過多的低頻分量導致很多時候收斂非常慢，所以使用 gaussian 核控制的轉置卷積方法 平衡網絡收斂效率的問題。
4. 怎么Early stopping 減少迭代次數？ --> 使用模糊度與銳度的比值的導數進行衡量

優點

• 將GAN 譜優化的策略放到DIP之中，在頻率域中分析各個層的性質：低頻收斂快，高頻收斂慢。
• 用譜偏置的思路解釋了網絡退化問題
• 提出頻帶一致性、模糊度和銳度比值梯度 平衡了DIP收斂效率和效果

改進方向

• 就個人觀點：噪聲這里假設都是高頻的，但是低頻噪聲、結構噪聲是否會有影響？
• 該研究給實際應用DIP提供了很大的可能性，但是就實驗效果來看并沒有提升，甚至有所下降。所以基于這種方法怎么去同時提高效果？
• 就我個人想法：繼續減少參數化網絡的參數量（PIP等工作），并且提高恢復的效果（持續研究方向） 是現在的研究方向。