? ? ? ? EM, ExpectationMaximization Algorithm, 期望最大化算法。一種迭代算法，用于含有隱變量(hidden variable)的概率參數模型的最大似然估計或極大后驗概率估計，其概率模型依賴于無法觀測的隱變量。
? ? ? ? 經常用在ML與計算機視覺的數據聚類領域。
? ? ? ? EM應用：GMM混合高斯模型、聚類、HMM隱馬爾科夫模型等。
?
一、Jesen不等式
? ? ? ? 對于凸函數（對于所有實數x，有f’’(x)≥0）。當x時向量時，如果其hessian矩陣H是半正定的（H≥0），那么f是凸函數。如果f’’(x)＞0或者H＞0，那么f是嚴格凸函數。
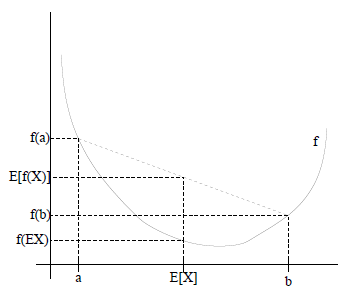
? ? ? ? 關于Jesen不等式：如果f是凸函數，x是隨機變量，那么有
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? E[f(x)]≥ f(Ex)
? ? ? ? 圖形化的表示方法就是：
二、EM原理
? ? ? ? 最大期望個算法經過兩個步驟交替進行計算
? ? ? ? ? ? ? ?step1: 計算期望E，利用對隱藏變量的現有估計值，計算其最大似然估計值。
? ? ? ? ? ? ? ?step2: 最大化M，最大化在E步上求得的最大似然值來計算參數值。
? ? ? ? （M步上找到的參數估計值被用于下一個E步計算中，這個過程不斷交替進行）
?
三、EM算法流程
1. 初始化分布參數
2. 重復直到收斂：
? ? ? ? ?E步驟：估計位置參數的期望值，給出當前的參數估計
???????? M步驟：重新估計分布參數，以使得數據似然性最大，給出位置變量的期望估計。
?
EM是一種解決存在隱含變量優化問題的有效方法，既然不能直接最大化L(o)，可以不斷建立l的下界（E步），然后優化下界（M步）。
