【轉】漫談ANN(2)：BP神經網絡

上一次我們講了M-P模型，它實際上就是對單個神經元的一種建模，還不足以模擬人腦神經系統的功能。由這些人工神經元構建出來的網絡，才能夠具有學習、聯想、記憶和模式識別的能力。BP網絡就是一種簡單的人工神經網絡。我們的第二話就從BP神經網絡開始漫談吧。

BP的來源

“時勢造英雄”，一個偉大的人物的登場總是建立在歷史的需求之下，所以我們剖析一個人，得先看看他的出身時代。同樣的道理，在講BP網絡的特性和用途之前，我們需要先了解一下它的來源和誕生原因，以便理解它的重要性。

1.1 最簡單的神經網絡結構——感知器

在1958年,美國心理學家Frank Rosenblatt提出一種具有單層計算單元的神經網絡,稱為感知器(Perceptron)。它其實就是基于M-P模型的結構。我們可以看看它的拓撲結構圖。

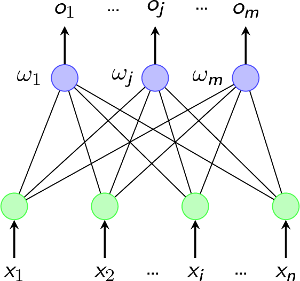
這個結構非常簡單，如果你還記得前面所講的M-P神經元的結構的話，這個圖其實就是輸入輸出兩層神經元之間的簡單連接（如果忘了可以看看第一話的模型示意圖）。

由第一話的(2)中我們知道輸入層各節點的輸入加權和

n e t' j = \sum i = 1 n ω i j x i

我們一般采用符號函數來當作單層感知器的傳遞函數，即輸出

o j = s g n (n e t' j ? T j) = s g n (\sum i = 0 n ω i j x i) = s g

公式(2)可以進一步表達為：

o j = {1 ? 1,, W T j X > 0 W T j X <

1.2 風中之燭——單層感知器的局限性

雖然單層感知器簡單而優雅，但它顯然不夠聰明——它僅對線性問題具有分類能力。什么是線性問題呢？簡單來講，就是用一條直線可分的圖形。比如，邏輯“與”和邏輯“或”就是線性問題，我們可以用一條直線來分隔0和1。

1）邏輯“與”的真值表和二維樣本圖如圖2：

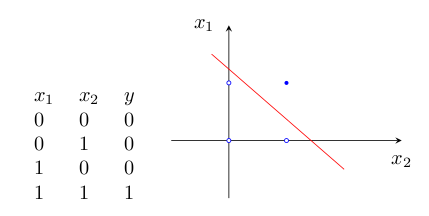
2）邏輯“或”的真值表如圖3：

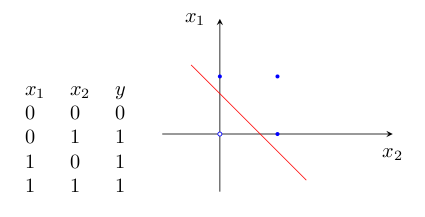
為什么感知器就可以解決線性問題呢？這是由它的傳遞函數決定的。這里以兩個輸入分量?

o j = {1 ? 1,, ? ? ? ω 1 j x 1 + ω 2 j x 2 ?

所以，方程

ω 1 j x 1 + ω 2 j x 2 ? T j = 0

確定的直線就是二維輸入樣本空間上的一條分界線。對于三維及更高維數的推導過程可以參考其他的Tutorials。

如果要讓它來處理非線性的問題，單層感知器網就無能為力了。例如下面的“異或”，就無法用一條直線來分割開來，因此單層感知器網就沒辦法實現“異或”的功能。

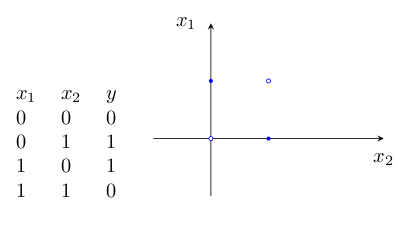
僅對線性可分問題具有分類能力，這就是單層感知器的局限所在。顯然它能夠解決的實際問題是很有限的。也正因為這樣，單層感知器在解決實際問題時很少被采用。

1.3 心有余而力不足——多層感知器的瓶頸

既然一條直線無法解決分類問題，當然就會有人想到用彎曲的折線來進行樣本分類。我們常常聽到一句批評人笨的話“你這人腦袋就是不會轉彎！”大意就是如此，腦袋會轉彎的人才善于解決問題。所以，人們請來了單層感知器他哥——多層感知器來幫忙。所謂多層感知器，就是在輸入層和輸出層之間加入隱層，，以形成能夠將樣本正確分類的凸域。多層感知器的拓撲結構如圖5所示。

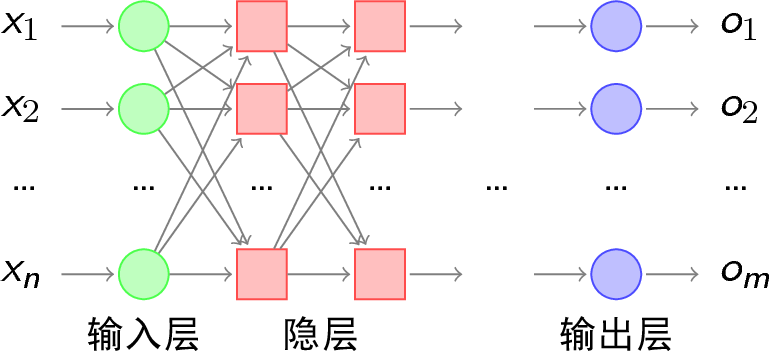
我們可以比較一下單層感知器和多層感知器的分類能力：

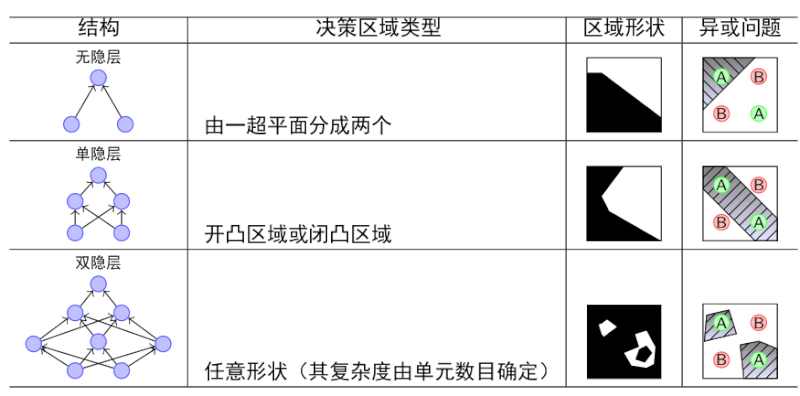
由上圖可以看出，隨著隱層層數的增多，凸域將可以形成任意的形狀，因此可以解決任何復雜的分類問題。實際上，Kolmogorov理論指出：雙隱層感知器就足以解決任何復雜的分類問題。

多層感知器確實是非常理想的分類器，但問題也隨之而來：隱層的權值怎么訓練？對于各隱層的節點來說，它們并不存在期望輸出，所以也無法通過感知器的學習規則來訓練多層感知器。因此，多層感知器心有余而力不足，雖然武功高強，但卻無力可施。

1.4 山重水復疑無路——ANN的低潮期

1966年，Minisky和Papert在他們的《感知器》一書中提出了上述的感知器的研究瓶頸，指出理論上還不能證明將感知器模型擴展到多層網絡是有意義的。這在人工神經網絡的歷史上書寫了極其灰暗的一章。對ANN的研究，始于1890年開始于美國著名心理學家W.James對于人腦結構與功能的研究，半個世紀后W.S.McCulloch和W.A.Pitts提出了M-P模型，之后的1958年Frank Rosenblatt在這個基礎上又提出了感知器，此時對ANN的研究正處在升溫階段，《感知器》這本書的出現就剛好為這剛剛燃起的人工神經網絡之火潑了一大盆冷水。一時間人們仿佛感覺對以感知器為基礎的ANN的研究突然間走到盡頭，看不到出路了。于是，幾乎所有為ANN提供的研究基金都枯竭了，很多領域的專家紛紛放棄了這方面課題的研究。

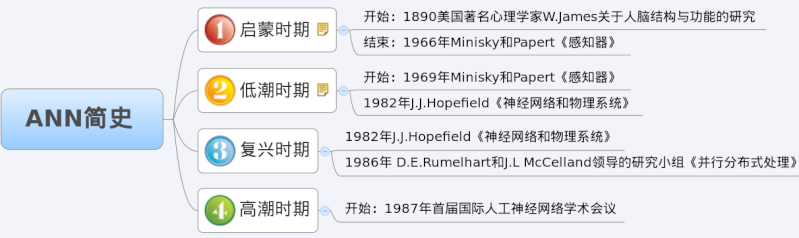
1.5 柳暗花明又一村——ANN研究的復蘇和BP神經網絡的誕生

所以說真理的果實總是垂青于能夠忍受寂寞的科學家。盡管ANN的研究陷入了前所未有的低谷，但仍有為數不多的學者忍受住寂寞，堅持致力于ANN的研究。在長達10年的低潮時期之間，相繼有一些開創性的研究成果被提出來，但還不足以激起人們對于ANN研究的熱情。一直到上世紀80年代，兩個璀璨的成果誕生了：1982年美國加州理工學院的物理學家John J.Hopfield博士的Hopfield網絡和David E.Rumelhart以及James L.McCelland研究小組發表的《并行分布式處理》。這兩個成果重新激起了人們對ANN的研究興趣，使人們對模仿腦信息處理的智能計算機的研究重新充滿了希望。

前者暫不討論，后者對具有非線性連續變換函數的多層感知器的誤差反向傳播(Error Back Propagation)算法進行了詳盡的分析，實現了 Minsky 關于多層網絡的設想。Error Back Propagation算法的簡稱就是BP算法，以BP算法實現的多層感知器網絡就是BP網絡。

所以，BP網絡本質上并不是一個新的網絡，而是使用BP學習算法的多層感知器網絡。

BP算法的基本思想

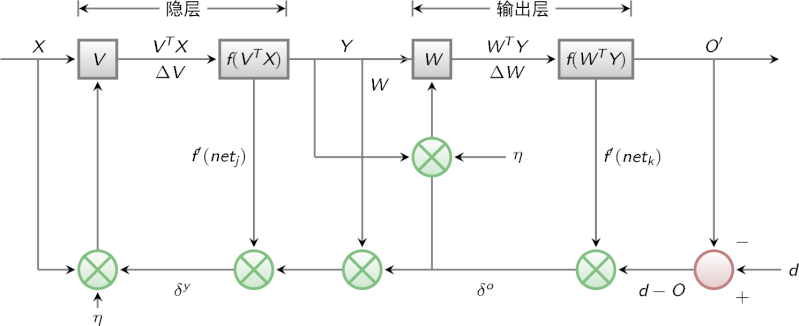
前面我們說到，多層感知器在如何獲取隱層的權值的問題上遇到了瓶頸。既然我們無法直接得到隱層的權值，能否先通過輸出層得到輸出結果和期望輸出的誤差來間接調整隱層的權值呢？BP算法就是采用這樣的思想設計出來的算法，它的基本思想是,學習過程由信號的正向傳播與誤差的反向傳播兩個過程組成。

正向傳播時,輸入樣本從輸入層傳入,經各隱層逐層處理后,傳向輸出層。若輸出層的實際輸出與期望的輸出(教師信號)不符,則轉入誤差的反向傳播階段。
反向傳播時，將輸出以某種形式通過隱層向輸入層逐層反傳,并將誤差分攤給各層的所有單元,從而獲得各層單元的誤差信號,此誤差信號即作為修正各單元權值的依據。

圖8就是BP算法的信號流向圖。

BP網絡特性分析——BP三要素

我們分析一個ANN時，通常都是從它的三要素入手，即1)網絡拓撲結構；2)傳遞函數；3)學習算法。如圖9所示。

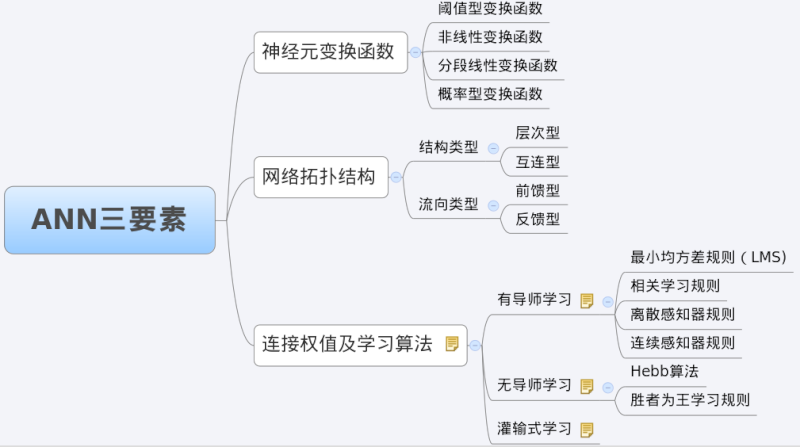
每一個要素的特性加起來就決定了這個ANN的功能特性。所以，我們也從這三要素入手對BP網絡的研究。

3.1 BP網絡的拓撲結構

前面已經說了，BP網絡實際上就是多層感知器，因此它的拓撲結構和多層感知器的拓撲結構（圖5）相同。由于單隱層（三層）感知器已經能夠解決簡單的非線性問題，因此應用最為普遍。三層感知器的拓撲結構如圖10所示。

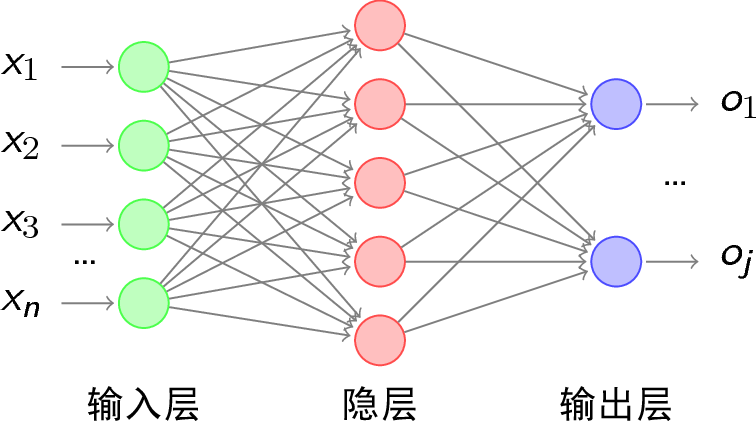
3.2 BP網絡的傳遞函數

BP網絡采用的傳遞函數是非線性變換函數——Sigmoid函數（又稱S函數）。其特點是函數本身及其導數都是連續的，因而在處理上十分方便。為什么要選擇這個函數，等下在介紹BP網絡的學習算法的時候會進行進一步的介紹。S函數有單極性S型函數和雙極性S型函數兩種，單極性S型函數定義如下：

f (x) = 1 1 + e ? x

其函數曲線如圖11所示。

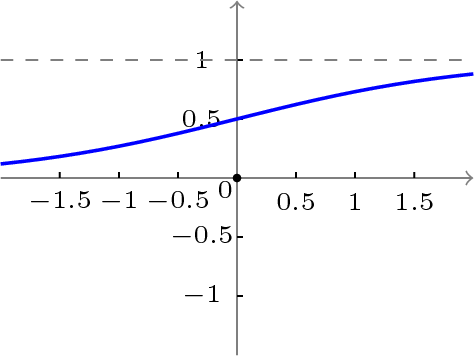
雙極性S型函數定義如下：

f (x) = 1 ? e ? x 1 + e ? x

其函數曲線如圖12所示。

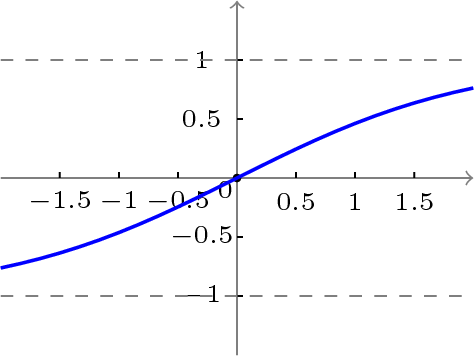
3.3 BP網絡的學習算法

BP網絡的學習算法就是BP算法，又叫?

E = 1 2 ( d ? O ) 2 = 1 2 \sum κ = 1 ? ( d k ? o k )

將以上誤差定義式展開至隱層，有

E = 1 2 \sum κ = 1 ? [ d κ ? f ( n e t κ ) ] 2 = 1

進一步展開至輸入層，有

E = 1 2 \sum κ = 1 ? { d κ ? f [ \sum j = 0 m ω j κ f (

由上式可以看出，網絡輸入誤差是各層權值

Δ ω j κ = ? η ? E ? ω j κ j = 0 , 1 , 2 , \dots , m ; κ = 1 , 2

Δ υ i j = ? η ? E ? υ i j i = 0 , 1 , 2 , \dots , n ; j = 1 , 2

對于一般多層感知器，設共有?

輸出層

Δ ω h + 1 j κ = η δ h + 1 κ y h j = η (d κ ? o κ) o κ

第?

Δ ω h i j = η δ h j y h i ? 1 = η (\sum l κ = 1 δ o κ ω h

按以上規律逐層類推，則第一隱層權值調整公式

Δ ω 1 p q = η δ 1 q χ p = η (\sum m 2 r = 1 δ 2 r ω 2

容易看出，BP學習算法中，各層權值調整公式形式上都是一樣的，均由3個因素決定，即：

學習率?
本層輸出的誤差信號?
本層輸入信號?

其中輸入層誤差信號與網絡的期望輸出與實際輸出之差有關，直接反應了輸出誤差，而各隱層的誤差信號與前面各層的誤差信號有關，是從輸出層開始逐層反傳過來的。

可以看出BP算法屬于，這類算法常被稱為誤差的梯度下降算法。

綜上所述，BP三要素如圖13所示。

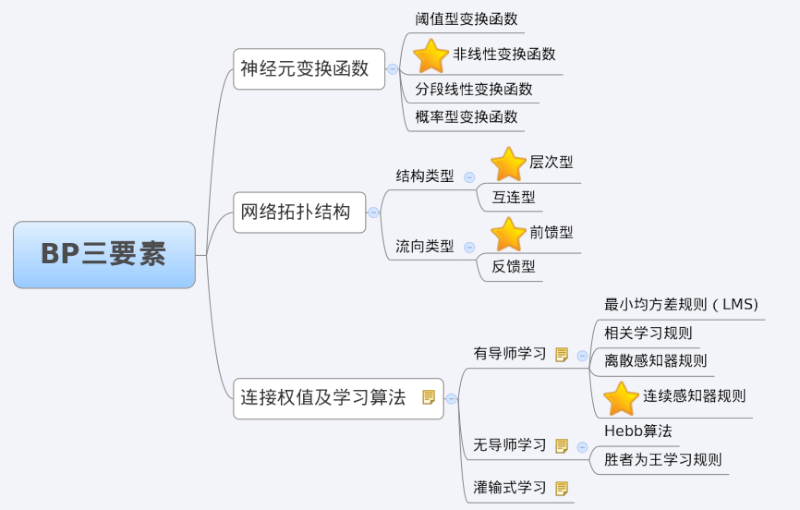
BP網實例

由于BP網絡具有出色的非線性映射能力、泛化能力和容錯能力，因此BP網絡成了至今為止應用最廣泛的人工神經網絡。圖14是Matlab下用BP網絡做線性擬合的結果，效果很好。

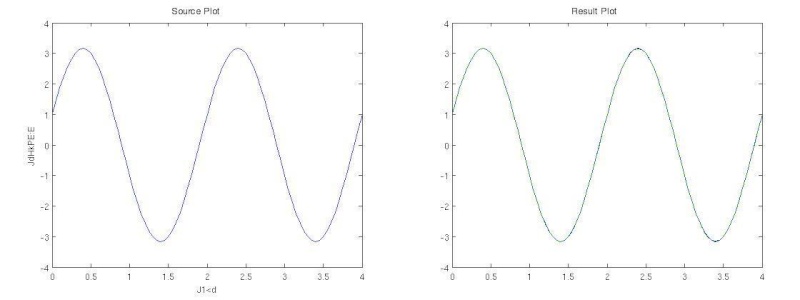
代碼如下：

% BP網絡函數逼近實例
% 1.首先定義正弦函數，采樣率為20Hz，頻率為1Hz
k = 1; % 設定正弦信號頻率
p = [0:0.05:4];
t = cos(k*pi*p) + 3*sin(pi*p);
plot(p, t, '-'), xlabel('時間'); ylabel('輸入信號');
% 2.生成BP網絡。用newff函數生成前向型BP網絡，設定隱層中神經元數目為10
% 分別選擇隱層的傳遞函數為 tansig，輸出層的傳遞函數為 purelin，
% 學習算法為trainlm。
net =
newff(minmax(p),[10,10,1],{'tansig','tansig','purelin'},'trainlm');
% 3.對生成的網絡進行仿真并做圖顯示。
y1 = sim(net,p); plot(p, t, '-', p, y1, '--')
% 4.訓練。對網絡進行訓練，設定訓練誤差目標為 1e-5，最大迭代次數為300，
% 學習速率為0.05。
net.trainParam.lr=0.05;
net.trainParam.epochs=1000;
net.trainParam.goal=1e-5;
[net,tr]=train(net,p,t);
%5.再次對生成的網絡進行仿真并做圖顯示。
y2 = sim(net,p);
plot(p, t, '-', p, y2, '--')