c++ 多重背包狀態轉移方程_動態規劃入門—

本文始發于個人公眾號：TechFlow，原創不易，求個關注

今天是周三算法與數據結構專題的第12篇文章，動態規劃之零一背包問題。

在之前的文章當中，我們一起探討了二分、貪心、排序和搜索算法，今天我們來看另一個非常經典的算法——動態規劃。

在acm-icpc競賽領域，動態規劃是一個非常大的范疇，當中包含了許多變種，而且很多變種難度極大。比如在各種樹上和圖上以及其他數據結構上做動態規劃，這會使得問題非常復雜。好在非競賽選手并不需要了解到那么深入，一般來說，吃透背包九講，就足夠笑傲各種面試了。所以周三的算法專題我們開始全新的篇章——背包系列，今天和大家分享背包九講中的第一講，也是最簡單的零一背包問題。

背包和零一背包

沒有競賽經驗的同學在看到這個標題的時候可能會一頭霧水，動態規劃和背包有什么關系。其實沒有關系，我也不是陳奕迅的粉絲，只是當初最經典的動態規劃問題用背包做了題面，還引發出了各種變種。后來在教學的時候為了方便，于是沿用了前人的名稱。

之前我們在怪盜基德偷寶石的問題當中提到過背包問題，其實很簡單，就是說我們當下有一個容量是V的背包，和n個體積分別是v[i]，價值是w[i]的五品。請問，在背包容量允許的前提下，我們最多能夠獲得多少價值的物品？

由于每種物品只有一個，也就是物品只有拿和不拿兩種狀態，所以這個問題被稱為零一背包問題。

貪心與反例

這種問題我們最先想到的就是貪心法，比如優先拿價值大的物品，或者是性價比高的物品，但是我們很容易構思出反例。

舉個例子，比如背包的容量是10，我們有3個物品，體積分別是6，5，5，價值是10，8，8。這個反例可以證明兩種貪心策略都不生效，因為價值最大的是10，它的體積是6，我們一旦拿了它就沒有空間再繼續獲取其他物品，而顯然拿兩個5的情況是最優的。同樣，體積是6的物品也是性價比最高的，性價比優先的貪心策略同樣不生效。

實際上不僅這兩種貪心策略不生效，所有能夠想到的貪心策略都不生效。這個問題看起來簡單，但是并不是那么容易解決。實際上這個問題一直困擾著計算學家，直到上世紀六十年代，動態規劃算法橫空出世，完美地解決了這個問題。

動態規劃

動態規劃算法的英文是dynamic programming，算是很直白的翻譯了。規劃我們都很好理解，但是動態應該怎么理解呢？又怎么來動態地規劃呢？關于這個問題的思考直接關系到算法的本質。

動態規劃算法的本質是狀態的記錄和轉移，我們結合剛才的問題，有沒有想過為什么貪心算法不可行？其實很簡單，因為我們沒辦法確定背包什么狀態是完美的。雖然我們知道背包的容量是V，但是我們并不知道最優的情況下我們能裝多少，最優的結束狀態是什么。我們把空間V看成了一個狀態來進行貪心，貪心得到的結果是最優的，但是只是貪心能達到的狀態的最優解，并不是全局的最優解，因為背包容量的限制，很有可能我們貪心策略下無法達到真正最優的狀態。

用剛才的例子解釋一下上面這段話，在貪心算法下，我們會選取容量是6，價值是10的物品，這個物品拿取了之后背包的狀態是6，獲取的價值是10。這個狀態是貪心能夠達到的最終狀態，對于這個狀態而言，它是最優解，但是這個狀態并不是整體最優的情況，因為在貪心策略下，無法達到容量10全用完的狀態。

理解了這個問題之后，再去推導解法就順其自然了。貪心策略可以獲取一些狀態最優的情況，那么我們能不能記錄下所有狀態能夠達到的最優的情況，最后在這些最優的情況當中選取一個最優的，它不就是整體最優解了嗎？

動態規劃正是基于上述思路展開的，它解決的不是一個狀態的最優解，而是所有狀態的最優解。

狀態與轉移

看到這里，你肯定還沒理解動態規劃算法，但是應該已經有一些大概的感覺了。這是對的，有正確的感覺是正確認識的前提。我們循序漸進，再來看狀態這個概念。

我們剛才提了這么多次，究竟狀態是什么呢？這是一個比較抽象的概念，在不同的問題當中它有著不同的含義。在背包問題當中，狀態指就的是背包容量的使用情況。由于背包問題中物品的體積是整數，顯然背包容量的可能性是有限的，這點不起眼，但是很重要，如果狀態不是整數，那么雖然存在動態規劃的可能，但是代碼實現可能比較麻煩。

明白了背包的容量是狀態之后，我們可以進一步想明白，背包的容量是會變化的。變化的原因是因為我們往里面放了東西，放了東西之后，背包的狀態會發生變化，會從一個狀態轉移到另一個狀態。狀態的轉移中間伴隨著我們放入東西，我們放的物品并不是固定的，而是有多種選擇的，我們決定放入A而不是BC，這是一種決策，決策會帶來狀態的轉移，不同的決策會帶來不同的轉移。

比如當前有一個背包，它的容量是10，我們在其中已經放入了一個體積是3，價值是7的物品。如果這個時候，我們經過選擇再放入一個體積是4，價值是5的物品。那么顯然，背包占用的容量會變成7，價值會變成12。這個過程就是一個經典的狀態轉移過程，這也是整個動態規劃算法的核心。

基本的概念和思想已經介紹完了，接下來就是用這些概念來解決實際問題了。

最優狀態

我們前文說了，動態規劃最后會獲取所有狀態的最優解，再從中選取全局最優的。那么它是怎么獲取局部最優解的呢？

在回答這個問題之前，我們先來思考兩個問題。

首先，假如我們已經知道了背包體積是3時的最大價值是5，這時候我們決定放入一個體積是4，價值是5的物品，那么背包的體積會增加到7，那么這個時候獲得的是體積6的最優解嗎？

這個問題不難回答，我們稍微想想就知道，很有可能不是。舉個最簡單的例子，假如我們有一個體積是7，價值是20的物品。那么顯然要比放這兩個物品更優。雖然狀態3最多能獲得價值5，狀態7也可以由狀態3轉移得到，但是這并不一定是最優的。也就是說最優的狀態轉移出去，并不一定也能得到其他狀態的最優值。

我們把問題反過來就不一樣了，如果我們知道了體積6的最優解，并且還知道它是由體積等于4轉移得到的，那么我們能不能確定體積4的狀態也是對應的最優解？

這次的答案就變了，是正確的，因為如果體積4時還有更好的解法，那么體積6理應也會變得更好才對，這和我們的假設矛盾了。

我們總結一下上面的兩個結論，也就是說局部最優的情況轉移出去并不一定是最優的，但是局部最優一定也是由其他局部最優的狀態轉移得到的。這句話有點像繞口令，但是我覺得應該不難解釋。就好比學霸去考試，不一定能考第一，但是考到第一的一定是學霸。局部最優就是學霸，轉移就是考試。局部最優轉移出去并不一定是轉移之后狀態的最優，有可能還有其他更好的轉移策略，但是對于某個狀態最優的情況而言，它一定也是從之前的某個最優狀態轉移得到的。

并且狀態的轉移也是有順序的，比如在這題當中，背包當中放入了物品體積只可能增加，不可能減小，意味著狀態只能從小的轉移到大的。

我們捋一捋思路，已經很明確了，狀態可以轉移，狀態的轉移有順序，局部最優一定是由其他局部最優轉移得到的。由于我們并不知道當前的轉移能否達到最優狀態，所以我們需要用一個數組或者是容器來記錄所有狀態歷史上曾經達到過的最值。最后從所有的最值當中再選出一個最值來，就是最后問題的解。

到這里，如果是一般的動態規劃問題，已經解決了，但是零一背包還有一個細節需要考慮。

無后效性

我們先來看下整個的計算流程，首先我們需要從最初狀態開始，這個最初的狀態很好辦，就是背包是空的時候，這時候的價值是0，體積也是0，這也是它的最優狀態，這個很好理解，因為我們不能無中生有。

所以我們從0開始轉移狀態，狀態轉移伴隨著決策，在這題當中體現在選取不同的物品上。我們遍歷物品，作為決策，再遍歷能夠應用這些決策的狀態，就拿到了所有的狀態轉移。最后，我們用一個容器記錄一下所有狀態轉移過程當中達到的局部最優解，于是就結束了。

這個過程看起來非常正常，沒有任何異常，但實際上，問題來了。

我們還用剛才的題面舉例，背包容量是10，3個物品，體積分別是6，5，5，價值是10，8，9。我們從0開始拿取第三個物品，轉移到了狀態5，此時的價值是9。這個時候，我們繼續往后遍歷的話還會遍歷到狀態5，它已經是拿取了物品3，價值9的信息了。因為一個物品只能拿一次，所以我們不能再用物品3轉移狀態5，否則就違反了題意。

你可能會說這個問題不難，我們可以在狀態當中也記錄之前做過的決策嘛，只要在決策的時候加一個判斷就好了。

表上面看是因為物品不能重復拿的限制，實際上是因為我們的狀態之間會有影響。也就是說我們前面做的決策很有可能影響后面的狀態做決策，這種狀態之間的前后影響稱為后效性。顯然在有后效性的場景下我們是不能使用動態規劃算法的，并不是所有問題都可以通過加上判斷解決，我們需要解決后效性這個本質問題，也就是說我們要想辦法消除后效性。

在這個問題當中，這一點很容易做到。我們只需要控制一下狀態和決策的遍歷順序，將之前的決策與之后的決策分開，使它們互不影響即可。如果我們先遍歷狀態，再遍歷每個狀態可以采取的措施，這樣必然會造成前后影響。因為前面做了的決定，后面就不能再做。但是后面并不能感知前面究竟做了什么決定。所以比較好的方法是先遍歷決策，再來遍歷可以采取這個決策的狀態。為了避免決策前后的互相影響，我們采取倒序的方式遍歷狀態。

我們舉個例子，假設背包容量還是10，我們枚舉的第一個物品體積是3，價值是5。我們倒敘遍歷狀態7到0，因為對于大于7的狀態而言，并不能采取這個決策（總體積會超）。因為對于大于7的狀態而言，我們不能采取這個決策（總體積會超過限制），對于狀態7而言，我們可以采取這個決策，轉移到狀態10。我們并不知道這樣轉移會不會達成最優，所以我們這樣來記錄：dp[10] = max(dp[10], dp[3] + 5).

我們接著遍歷體積6，可以轉移到狀態9。

由于我們是倒序遍歷，所以當我們用狀態7更新狀態10時，狀態7本身并沒有被這個決策更新過。即使后面我們在遍歷到狀態4時更新了狀態7，也不會影響狀態10的結果。因為是倒序遍歷的，我們不會再用同一個策略更新到狀態10了。如果是正序遍歷，則無法避免。同樣的物品，我們很有可能會出現，用狀態1更新狀態4，再用狀態4更新狀態7，再用狀態7更新狀態10的情況出現。而這種情況其實對應了使用了多個同樣的物品，這就和題意矛盾了。

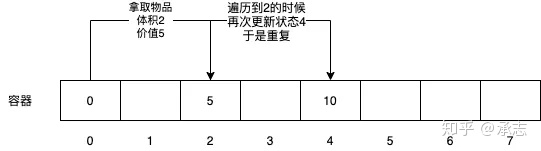
舉個例子，假設有一個物品體積是2，它的價值是5。我們遍歷狀態0的時候，會更新狀態2，我們遍歷到了狀態2，又用同樣的物品更新了狀態4，得到了10。那么對于狀態4而言，它其實相當于拿了2個這個物品，也就是說被同一個決策更新了兩次。但是我們的物品最多只有一個，顯然就不對了。