
?背景介紹
在日益信息化的社會中,各種各樣的嵌入式系統已經全面滲透到日常生活的每一個角落。嵌入式系統的功能越來越復雜,這就使得一個嵌入式系統產品從市場需求立項到方案選擇、樣機研制、定型量產所需要的開發費用越來越多,所需開發時間越來越長。因此,高效的嵌入式系統設計方法就顯得尤為重要。
1.1 傳統的嵌入式系統設計方法
嵌入式系統開發的關鍵就是對核心部分進行功能驗證。傳統的驗證方法是建模模擬和制作目標板評估。
通過建模來進行功能驗證存在不足。首先就是耗時和準確性互相矛盾。建立高層次的模型需要的時間短,但是模擬不夠準確。相反,低層次的模型可以達到滿意的評估效果,但是建模耗時長。其次,建模模擬是靜態的過程,不能很好地反映系統實際運行的情況。好的目標板,各部分連接已經固定。如果需要改動部分連接,只能重新設計制版。這樣一來就會大大延長產品的上市時間,還會增加開發費用。新推出的嵌入式系統產品,開始設計時比較難把所有的技術細節考慮清楚,有時甚至是邊設計邊修改性能指標,因此直接制作專用的目標板原型已經不太適合復雜的嵌入式系統產品的設計。
1.2 嵌入式系統模塊化設計方法
嵌入式系統設計要求做到可測性、高效性和靈活性。目前,嵌入式系統物理尺寸越來越小,功能越來越復雜。為了方便調試、維護系統,完全可測顯得極為重要。另一方面,模塊化的設計方法越來越引起人們的關注。模塊化設計方法將復雜的系統合理地劃分出不同的功能模塊,然后充分利用已有的模塊,設計新的模塊,最后將這些模塊連接起來組成目標系統。模塊化的設計方法減少全新的設計、降低開發難度、節省開發成本、縮短開發時間,是一種高效的嵌入式系統設計方法。另外,各個模塊連接的靈活性是非常重要的,它直接決定模塊的組合能力。
2 基于ARM核的快速原型化平臺
嵌入式系統硬件有如下特點:
1、嵌入式硬件以嵌入式處理器為核心。嵌入式處理器的種類眾多,功能各異。
2、相對嵌入式處理器,嵌入式系統外設的種類較少,接口標準也比較統一。
3、隨著EDA的發展,SOC(system on Chip)的應用越來越廣泛。
2.1 ARM核處理器的特點
ARM核處理器因為其低成本、低功耗、高性能的優點廣泛應用于嵌入式系統。基于ARM核處理器是高度集成的SOC,包括ARM核和各種各樣的外設。圖1是基于ARM核處理器的常見結構。存儲器控制接口為外接存儲器提供了總線接口。該總線接口支持不同種類的存儲器芯片以及不同的存儲操作。此外,還可以用該總線來擴展外設。片內外設包括中斷控制器.html“ target=”_blank“》控制器、OS定時器、UART、I2C、PWM和AC97等等。在這些片內外設中,有些信號是復用的,這樣做的好處是方便用戶使用。用戶如需要片內外設,只需要配置相關的寄存把片內外設連接到通用I/O即可,非常靈活,例如USB接口的服務器/客戶端。有些片內外設有專用的信號。用戶通過連接或者擴展這些通用I/O和專用I/O來使用片內外設。當片內外設不能完成目標系統的功能時,需要通過總線來擴展特殊的外設芯片。
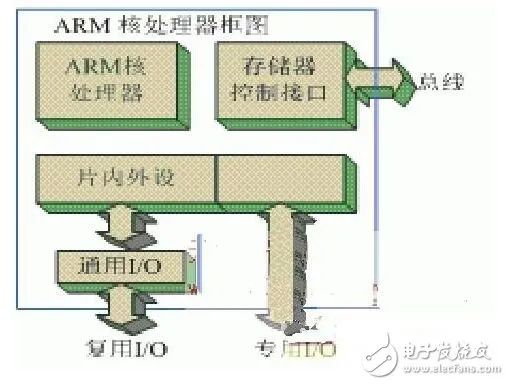
圖1(ARM核處理器框圖)
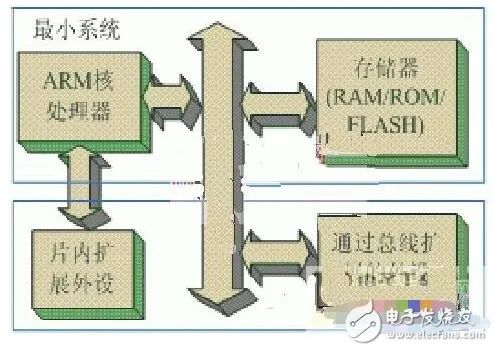
圖2 (ARM核處理器的嵌入式系統的框圖)
2.2 基于ARM的快速原型化平臺的實現
圖2是基于ARM核處理器的嵌入式系統的框圖。該系統分成兩個部分,一部分是最小系統,由嵌入式ARM核處理器和存儲器組成;另外一部分包括從嵌入式處理器片內外設接口直接擴展的外設和通過總線擴展的外設。為了充分利用模塊化設計方法,這些部分應該能夠通過靈活的互連組成一個平臺。靈活的互連功能由互連模塊完成。
可編程器件如CPLD和FPGA,可以在系統編程,修改連接只需要修改相應的控制程序即可,非常方便靈活。CPLD成本低,運行速度快,但是集成度比較低。FPGA集成度高,可以實現CPLD很難實現的復雜的邏輯功能,例如內嵌邏輯分析儀程序,獲取必要的信號,完成系統在線測試。FPGA另外一個優勢就是可以動態配置,例如系統上電時配置自檢程序,自檢通過后再配置實際工作的程序。最后,在FPGA里面嵌入CPU軟核,進行SOC的開發。所以可編程互連模塊選用FPGA來組成。
為了確定可編程互連模塊的插入位置,再來分析圖2嵌入式系統的結構。
最小系統決定了整個系統的處理能力,是整個系統的核心。常用的嵌入式處理器的時鐘周期已經高達400MHz,并且會進一步發展。連接處理器的總線速度和存儲器芯片的速度也超過了100MHz。FPGA引腳到引腳的延時是幾個納秒的數量級,所以FPGA模塊的插入會降低整個系統的處理速度。故在處理器和存儲器之間不能插入FPGA模塊。外設可以使得嵌入式系統和實際應用環境進行通信和交互操作。通常外設已經高度模塊化并且相互獨立,在外設之間幾乎不會有柔性連接的要求,而且處理器和外設之間的數據通信速度比最小系統的運行速度要慢很多。因此,用互連模塊取代最小系統和外設之間的直接物理連接是切實可行的。
按照這種思路,設計出了如圖3所示的快速原型化平臺。
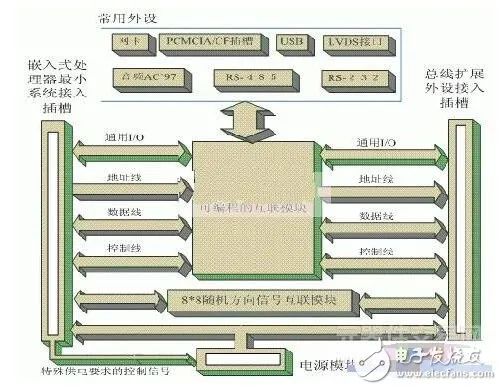
圖3(快速原型化平臺)
圖3中,可編程互連模塊是快速原型化平臺的核心部分。常用的外設部分包括:網卡,USB接口,LVDS接口,RS-232接口,rs-485/' target='_blank'>RS-485接口,音頻AC`97接口,PCMCIA/CF卡接口。這些常用外設就是前文提到的可重復利用的模塊。由于嵌入式處理器的總線、通用I/O、專用I/O和各種外設都連接在可編程互連模塊上,因此不同的嵌入式處理器只需要設計最小系統即可,然后將該最小系統接入快速原型化平臺,利用這個平臺提供的外設進行系統調試。
以上設計的快速原型化平臺,不僅考慮了當前嵌入式硬件系統的發展特點即嵌入式處理器種類多,外設種類相對較少,接口標準趨于統一,同時又充分體現了可測性、靈活性、模塊化的設計思想。
3 隨機方向信號的可配置互連
常見的信號傳輸方向不管是單向的還是雙向的,都可以預先確定。例如,數據總線是雙向的,讀或者寫是完全確定的,可以通過讀寫信號來控制數據的傳輸的方向。但是有一類特殊的總線,例如I2C,它是多主/從的通信總線。如圖4所示,如果設備1發起通信,則SCL上的信號傳輸方向是從設備1到設備2,如果是設備2作主設備發起通信,則SCL的上的信號傳輸方向剛好相反。系統設計中要求總線上可以雙向傳輸信號。FPGA內部由一系列的邏輯門組成,如果I2C 信號通過FPGA來連接的話,就不能正常工作。這是因為,雙向傳輸可以等效視為由兩個反并聯的門來實現(如圖5,用方向控制信號來確定實際的傳輸方向)。但是,I2C信號,沒有明確的方向控制信號,也就無法正確地通過圖5 所示結構的電路。
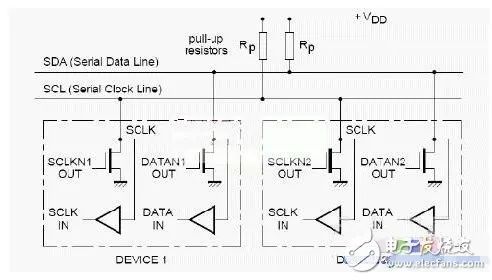
圖4(I2C總線)
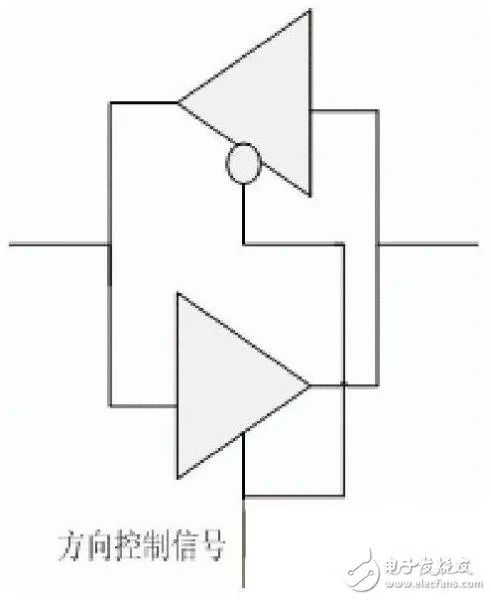
圖5(雙向信號傳輸)
如果直接布線或者跳線來連接I2C信號,就可以保證I2C正常工作,但是,這就和快速原型化平臺可配置互連的靈活性相違背,所以提出以下方案。I2C信號不經過FPGA來配置連接,而是通過基于MOSFET的數據開關。目前,市場上常用的點到點任意方向的MOSFET開關并不能直接使用。因為常見的結構是一路到多路或者多路到一路。利用CPLD來控制選通,多路并聯就可以組成8X8的點到點的隨機方向的可配置連接。是一路到八路的數據開關的內部結構。
來源:本文轉自網絡,版權歸原作者所有。















)





