深入理解softmax函數

　　Softmax回歸模型，該模型是logistic回歸模型在多分類問題上的推廣，在多分類問題中，類標簽? $\textstyle y$ ?可以取兩個以上的值。Softmax模型可以用來給不同的對象分配概率。即使在之后，我們訓練更加精細的模型時，最后一步也需要用softmax來分配概率。本質上其實是一種多種類型的線性分割，當類標簽? $\textstyle y$ ?取 2 時，就相當于是logistic回歸模型。

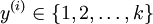　　在 softmax回歸中，我們解決的是多分類問題（相對于 logistic 回歸解決的二分類問題），類標? $\textstyle y$ ?可以取? $\textstyle k$ ?個不同的值（而不是 2 個）。因此，對于訓練集? $\{ (x^{(1)}, y^{(1)}), \ldots, (x^{(m)}, y^{(m)}) \}$ ，我們有? $y^{(i)} \in \{1, 2, \ldots, k\}$ 。（注意此處的類別下標從 1 開始，而不是 0）。例如，在 MNIST 數字識別任務中，我們有? 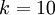$\textstyle k=10$ ?個不同的類別。

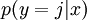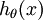　　對于給定的測試輸入? $\textstyle x$ ，我們想用假設函數針對每一個類別j估算出概率值? $\textstyle p(y=j | x)$ 。也就是說，我們想估計? $\textstyle x$ ?的每一種分類結果出現的概率。因此，我們的假設函數將要輸出一個? $\textstyle k$ ?維的向量（向量元素的和為1）來表示這? $\textstyle k$ ?個估計的概率值。具體地說，我們的假設函數? $\textstyle h_{\theta}(x)$ ?形式如下：

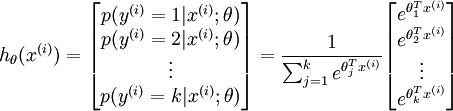
交叉熵代價函數

? ??

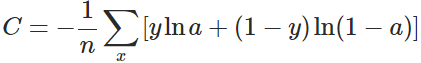
其中，x表示樣本，n表示樣本的總數。

這種代價函數與普通的二次代價函數相比，當預測值與實際值的誤差越大，那么參數調整的幅度就更大，達到更快收斂的效果。

證明如下：

?　?

?其中：

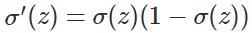
因此，w的梯度公式中原來的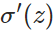被消掉了；另外，該梯度公式中的表示輸出值與實際值之間的誤差。所以，當誤差越大，梯度就越大，參數w調整得越快，訓練速度也就越快。同理可得，b的梯度為：

Softmax 回歸 vs. k 個二元分類器

如果你在開發一個音樂分類的應用，需要對k種類型的音樂進行識別，那么是選擇使用 softmax 分類器呢，還是使用 logistic 回歸算法建立 k 個獨立的二元分類器呢？

這一選擇取決于你的類別之間是否互斥，例如，如果你有四個類別的音樂，分別為：古典音樂、鄉村音樂、搖滾樂和爵士樂，那么你可以假設每個訓練樣本只會被打上一個標簽（即：一首歌只能屬于這四種音樂類型的其中一種），此時你應該使用類別數? $k ?= 4?的softmax回歸。（如果在你的數據集中，有的歌曲不屬于以上四類的其中任何一類，那么你可以添加一個“其他類”，并將類別數? k ?設為5。）$

如果你的四個類別如下：人聲音樂、舞曲、影視原聲、流行歌曲，那么這些類別之間并不是互斥的。例如：一首歌曲可以來源于影視原聲，同時也包含人聲。這種情況下，使用4個二分類的 logistic 回歸分類器更為合適。這樣，對于每個新的音樂作品，我們的算法可以分別判斷它是否屬于各個類別。

現在我們來看一個計算視覺領域的例子，你的任務是將圖像分到三個不同類別中。(i) 假設這三個類別分別是：室內場景、戶外城區場景、戶外荒野場景。你會使用sofmax回歸還是 3個logistic 回歸分類器呢？ (ii) 現在假設這三個類別分別是室內場景、黑白圖片、包含人物的圖片，你又會選擇 softmax 回歸還是多個 logistic 回歸分類器呢？

在第一個例子中，三個類別是互斥的，因此更適于選擇softmax回歸分類器。而在第二個例子中，建立三個獨立的 logistic回歸分類器更加合適。

轉載于:https://www.cnblogs.com/xiaobaituyun/p/7892729.html

本文來自互聯網用戶投稿，該文觀點僅代表作者本人，不代表本站立場。本站僅提供信息存儲空間服務，不擁有所有權，不承擔相關法律責任。
如若轉載，請注明出處：http://www.pswp.cn/news/370482.shtml
繁體地址，請注明出處：http://hk.pswp.cn/news/370482.shtml
英文地址，請注明出處：http://en.pswp.cn/news/370482.shtml

如若內容造成侵權/違法違規/事實不符，請聯系多彩編程網進行投訴反饋email:809451989@qq.com，一經查實，立即刪除！