本文屬于 dotnet 代碼優化系列博客。相信大家都對圈復雜度這個概念很是熟悉,本文來和大家聊聊邏輯的圈復雜度。代碼優化里面,一個關注的重點在于代碼的邏輯復雜度。一段代碼的邏輯復雜度越高,那么維護起來的難度也就越大。衡量代碼的邏輯復雜度的一個維度是通過邏輯圈復雜度進行衡量。本文將告訴大家如何判斷代碼的邏輯圈復雜度以及一些降低圈復雜度的套路,讓大家了解如何寫出更好維護的代碼
回顧一下代碼設計的目標,其中一個很重要的點就是解決 復雜的代碼邏輯 和 人類有限的智商 的矛盾。假設人類的智商非常的高,無論再復雜的代碼邏輯都能理解,且人類寫出的邏輯也不存在漏洞,那其實很多代碼設計都是不需要的。現實剛好不是,一個稍微復雜的項目,就已經不是人類輕而易舉能夠掌控的。即使是自己編寫的代碼,也會隨著時間逐漸遺忘代碼里面當初的實現邏輯。何況在團隊協作中,可能會遇到需要閱讀其他開發者留下的代碼的時候,假設前輩們沒有好好的進行編寫和設計,自然可能是給后來者挖了一個大坑
邏輯的圈復雜度屬于一個度量代碼復雜度的維度,但稍微特別的是,當邏輯的圈復雜度比較低時,能意味著代碼復雜度比較低,比較好維護。但反過來不成立,比較好維護的代碼,不一定是邏輯的圈復雜度比較低的代碼。代碼的可維護是需要綜合考慮多個維度的,雖然說降低邏輯的圈復雜度基本上都是屬于正確的事情,但由于實際項目遇到的情況比較特殊,還請識別主次矛盾,不要強行優化
邏輯的圈復雜度是指在代碼執行過程中,邏輯上形成的圈的數量,更多的是指在面向對象設計里面的類和方法之間的關系。至于方法內的循環判斷等,只屬于(代碼)圈復雜度(Cyclomatic complexity)而不是邏輯圈復雜度
學術的定義,相信大家都不感興趣,下面來舉一個例子,相信大家看完很快就懂了
例子依然是老套的圖書管理系統的故事,假定書籍有 人文、哲學、物理、數學、計算機 等類型的書籍,在圖書管理系統里面,需要有一定的業務邏輯,對其進行處理。其工序有些是所有類型共用的,有些是需要根據類型而來的,假定每個工序都能用一個代碼方法完成。原始的邏輯設計抽象起來如下圖
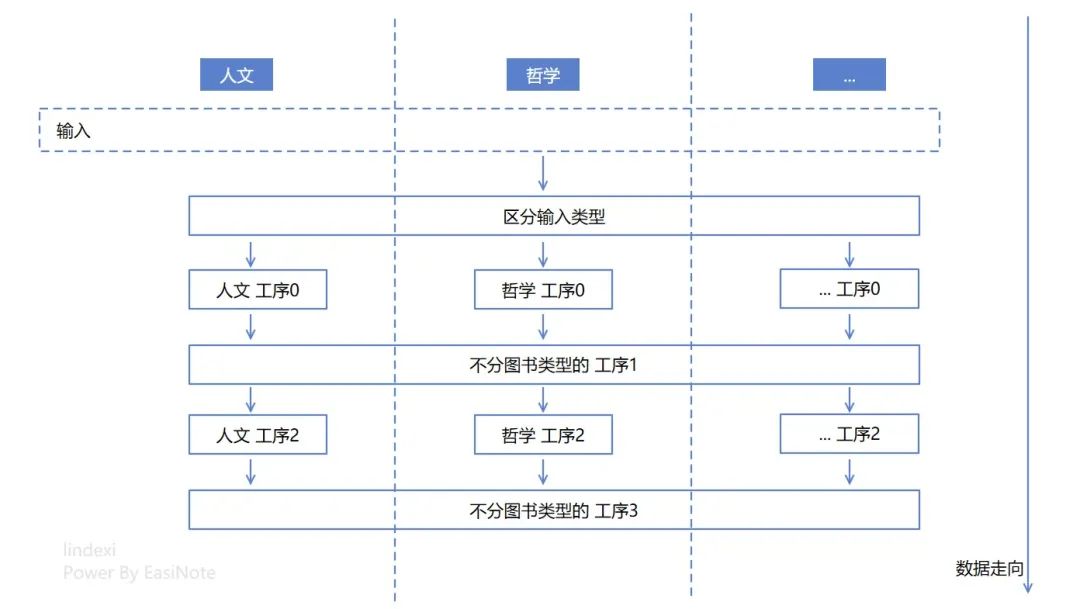
從邏輯上看,以上的邏輯設計是存在很多個圈圈的,相當于不停的拆分、聚合,每一次都是在增加邏輯圈復雜度,這樣的邏輯設計對應到代碼里面,大概就是一堆 if 或者 switch 判斷,控制其后續走向,或者是面向對象的繼承關系,讓調用穿插在基類和子類之間。假定以上的邏輯設計屬于使用了 一堆 if 或者 switch 判斷的方式,那自然在區分輸入類型和工序1里面,都會存在判斷書籍類型,以調用后續邏輯的代碼,偽代碼如下
void 區分輸入類型()
{if (書籍類型 == 人文){人文_工序0();}else if (書籍類型 == 哲學){哲學_工序0();}else if(...){...}
}void 人文_工序0()
{// 工序的邏輯...不分圖書類型的_工序1();
}void 哲學_工序0()
{// 工序的邏輯...不分圖書類型的_工序1();
}void 不分圖書類型的_工序1()
{// 工序的邏輯...if (書籍類型 == 人文){人文_工序2();}else if (書籍類型 == 哲學){哲學_工序2();}else if(...){...}
}...從以上的偽代碼也可以看到,在?區分輸入類型?和?不分圖書類型的_工序1?之間,存在邏輯比較相似的代碼,那就是拆分書籍類型,然后調用不同的方法。當書籍的類型足夠多的時候,這個邏輯維護起來就開始令人煩躁起來了,當工序同樣多起來的時候,那就更加不好玩咯
來數數邏輯的圈圈數量,猜猜有多少個圈圈?如下圖標記出來的只有 4 個圈圈對不
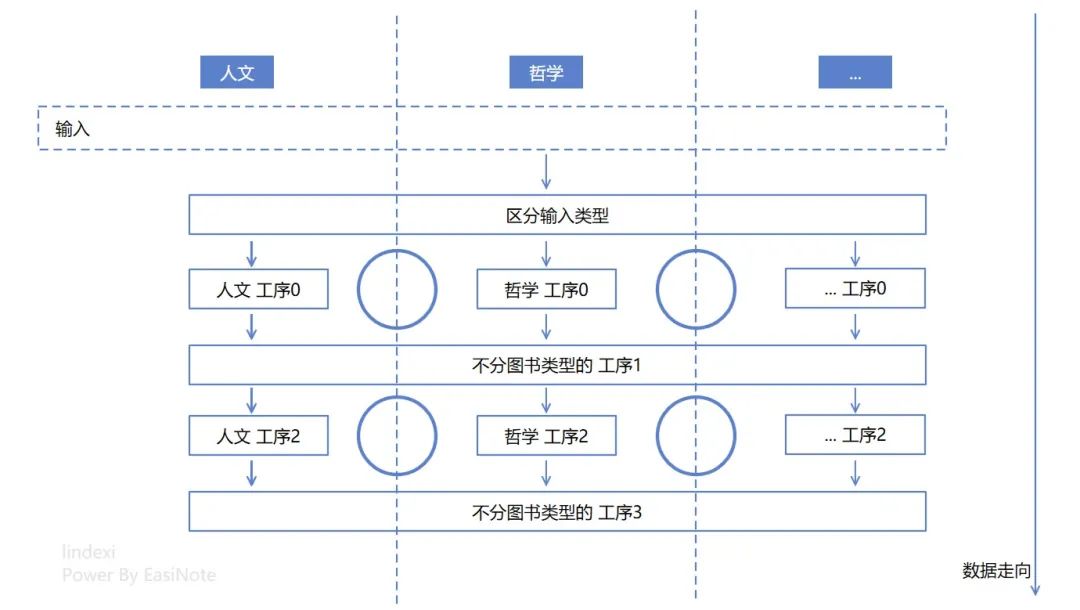
其實沒有那么簡單。嗯,不嚴謹的算,上面的邏輯設計圖至少有 9 個圈圈
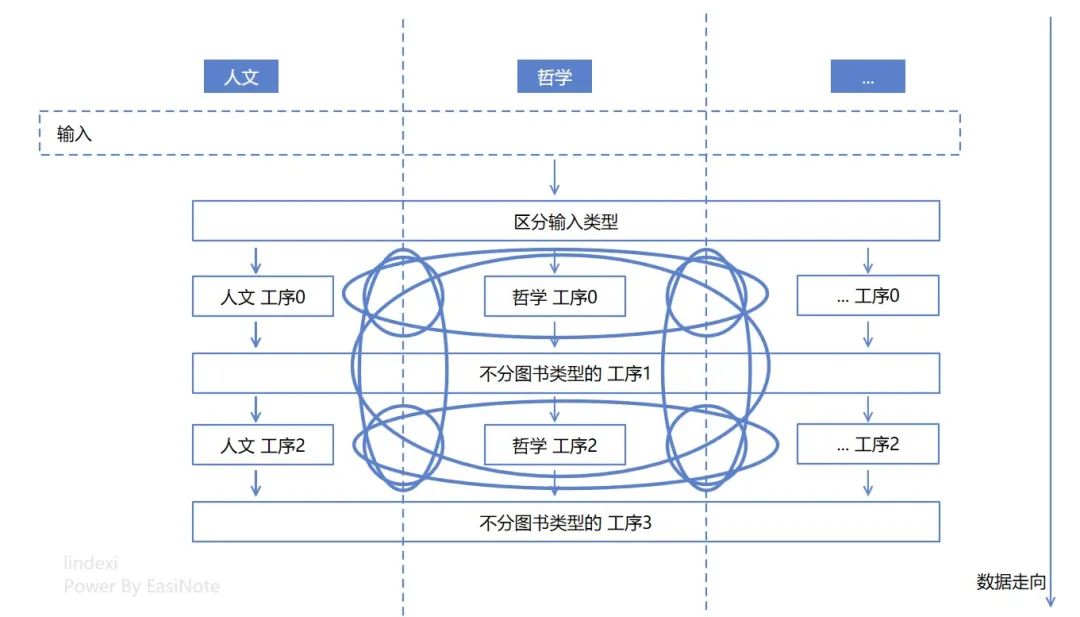
如果列出更多的書籍類型,以及更多的工序,那這個圈的數量能夠更加龐大
大家也可以想想看,每加一個書籍類型,會加多少個圈圈?世界上還有一群專家也在研究加一個模塊或一個功能時,圈復雜度的增加速率。在某些時候的設計上,會導致加一個模塊或加一個功能時,增加的圈圈數量會越來越多。例如上面的邏輯設計圖在兩個書籍類型,也就是兩個模塊時,只有三個圈圈,但是在有三個模塊時,就有 9 個圈圈了。也可以看到,隨著書籍類型的數量,也就是模塊的數量,不斷增加的時候,每加一個時,增加的圈圈數量會越來越多,這也就表示了邏輯復雜度每次增加都會越來越多
換一句話說,如果按照上面的邏輯設計圖的方式進行開發,會發現越開發越復雜。即使開發者有著很好的編寫代碼的能力,也會逐漸發現整個項目越來越難以掌控。在設計上存在將會導致必然出現的代碼邏輯圈復雜度時,會導致項目在開發過程中是上帝和程序猿才能看懂代碼,開發一定時間之后,就只有上帝才能看懂代碼了
在了解基礎的知識之后,大家也許會問,那如何改造降低圈復雜度呢?一個套路方法就是在區分類型之后,讓數據的走向被具體類型進行控制,這也是面向對象里,多態的一個用法。具體來做就是在 區分輸入類型 的類型之后,進入某個類型的書籍的總處理方法,在某個類型的總處理方法里面,可以愉快的從工序的開始執行到工序的結束
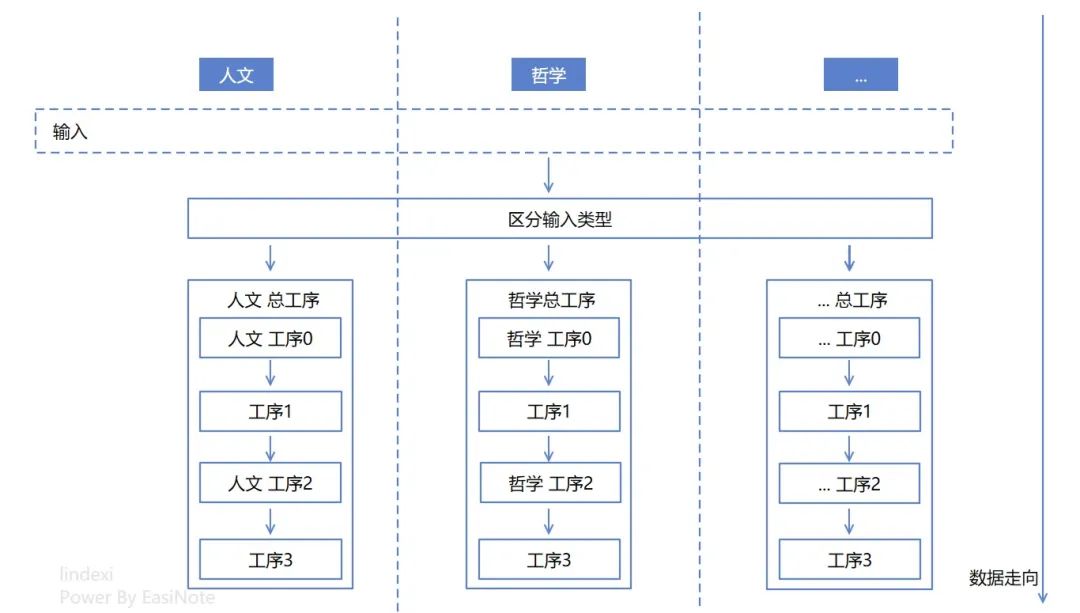
再來數一下邏輯的圈復雜度,是不是一個圈也數不到了?對應的代碼大概如下,可以看到每個總工序里面處理的邏輯一目了然
void 人文_總工序()
{人文_工序0();工序1();人文_工序2();工序3();
}void 哲學_總工序()
{哲學_工序0();工序1();哲學_工序2();工序3();
}啥都不用說,對比代碼量就知道,看代碼的清晰程度也能看起來降低圈復雜度之后的優化
那這時,也許有伙伴說,如果各個總工序都十分相似,是不是也可以再抽一下?是的,但是也需要看情況,如果少部分的重復邏輯可以帶來更多的代碼清晰度,那這部分的邏輯留著也是可以接受的。但如果在抽一下基礎類型之后,發現邏輯依然清晰,那就開干吧,畢竟重復的邏輯也不是什么好的事情
定義一個書籍處理的抽象基類,然后在此基類里面放總工序,接著各個具體的書籍處理類型,繼承基類,編寫實現方法,偽代碼如下
abstract class 書籍管理基類
{public void 總工序(){工序0();工序1();工序2();工序3();}protected abstract void 工序0();private void 工序1(){// ...}protected abstract void 工序2();private void 工序3(){// ...}
}class 人文書籍管理 : 書籍管理基類
{protected override void 工序0(){人文_工序0();}private void 人文_工序0(){// ...}protected override void 工序2(){人文_工序2();}private void 人文_工序2(){// ...}
}class 哲學書籍管理 : 書籍管理基類
{protected override void 工序0(){哲學_工序0();}private void 哲學_工序0(){// ...}protected override void 工序2(){哲學_工序2();}private void 哲學_工序2(){// ...}
}可以看到,這大概也就是一個超級簡單的框架了,具備了一定的擴展性,也就是后續如果還需要加上新的書籍類型,也是非常方便的,只需要定義多一個類型即可,同時邏輯上也相對來說比較清真,沒有那么復雜
以上是借助 C# 里面的抽象類實現的,這個套路需要不斷讓子類型進行重寫方法,導致邏輯上可能部分是在基類,部分是在子類。不過以上的代碼寫法是沒有問題的,因為繼承關系才只有兩層,但如果繼承關系更多了呢?假設有三層甚至更高呢?這時執行邏輯可能需要跨越多個類型,那邏輯復雜度也會上來
假定有如下圖的邏輯,需要按照順序或者是執行時間,分別調用方法1到6來完成業務端的任務。當存在讓子類型層層繼承的基類有三個的時候,如果調用方法散落在這個基類里面,那邏輯復雜度將會是非常高的,很多時候靜態閱讀代碼都非常有難度
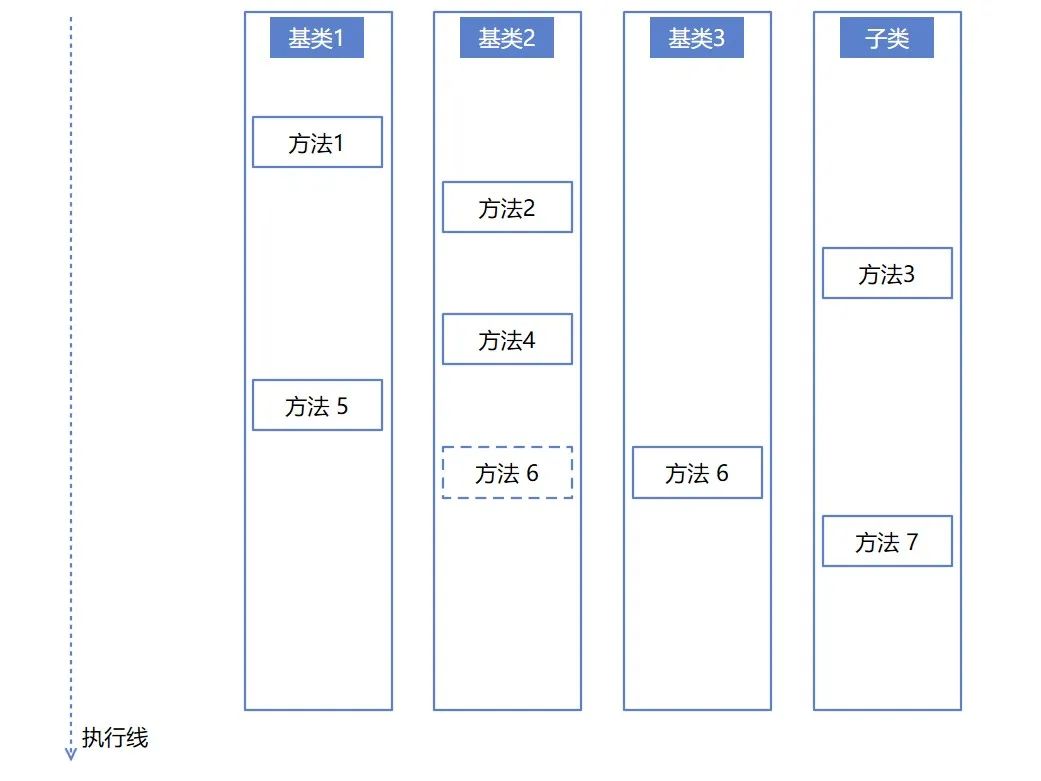
如上圖,假設以上沒有畫出來圖,而是寫成代碼,那想要靜態閱讀代碼,了解其中的執行邏輯,預計看了一會開始亂了,不知道對應的方法應該在哪個類型里面,哪個文件里面。好在 C# 里面禁用了多類型繼承,否則能寫出連示意圖畫出來都能勸退人的代碼。可是 C# 里面也有一個叫虛方法的定義,允許在基類里面定義虛方法,看子類的心情去進行重寫,有重寫就使用子類的,沒重寫就采用基類的,上圖里面的方法 6 是一個虛方法,在基類 2 里面定義,但是在 基類 3 被重寫。這時將會發現靜態閱讀的代碼,不見得就是實際運行的代碼。例如閱讀到基類 2 里面定義了方法 6 的邏輯,然而實際運行的時候,執行的是基類 3 的邏輯
這里需要補充一點的是靜態閱讀代碼指的是和調試閱讀代碼相對的閱讀代碼方式,指的是在不開始進行調試的方式進行閱讀代碼,可以在 IDE 的輔助下,例如在 VisualStudio 這樣的 IDE 輔助下閱讀代碼。好維護的代碼是需要考慮靜態閱讀代碼的,因為很多時候調試的時候能跑的路徑不會特別全,也不會特別多,甚至有些邏輯是存在很多前置條件的,僅靠調試來了解執行方式,可能了解到不全面
這也是某些開發老司機會說的“組合由于繼承”的其中一點原因,大量的繼承將會導致邏輯散落在各地,不夠“內聚”導致邏輯復雜度上升。值得一提是 “組合由于繼承” 這句話是具備大量前提的,還請不要將這句話作為開發的規范
那什么時候應該選擇什么方法?其實十分主觀,我的推薦是多試試看,寫多了,然后將自己坑多了,自然就知道了。主動去看自己之前寫過的復雜邏輯(最好別去看別人的,否則心態可能會炸)看看是否會感覺自己無法理解邏輯,如果會的話,再想想可以使用什么方式,如果再寫一次的話,可以更加方便閱讀代碼理清邏輯
回顧一下,本文告訴了大家什么是代碼邏輯圈復雜度,以及降低邏輯圈復雜度的套路方法。同時也告訴了大家,這個套路也不是萬能的,做的不好也可以提升代碼復雜度.






)

智能引號)



)






