位圖法

???? 判斷集合中存在重復是常見編程任務之一，當集合中數據量比較大時我們通常希望少進行幾次掃描，這時雙重循環法就不可取了。位圖法比較適合于這種情況，它的做法是按照集合中最大元素max創建一個長度為max+1的新數組，然后再次掃描原數組，遇到幾就給新數組的第幾位置上1。如遇到5就給新數組的第六個元素置1，這樣下次再遇到5想置位時發現新數組的第六個元素已經是1了，這說明這次的數據肯定和以前的數據存在著重復。這種給新數組初始化時置零其后置一的做法類似于位圖的處理方法故稱位圖法。它的運算次數最壞的情況為2N。如果已知數組的最大值即能事先給新數組定長的話效率還能提高一倍。Bloom filter可以看做是對bit-map的擴展。下面為利用位圖法實現整形數組的排序代碼。

 public class BitmapSort {
?
 /**
  * 使用位圖法進行排序
  * 找到最小值和最大值，申請位圖數組，對應位賦值為1，最后依次輸出。
  *  @param  arr
  */
 public static void bitmapSort(int[] arr) {
     int max = arr[0];
     int min = max;
     for (int i : arr) {
         if (max < i) {
             max = i;
         }
         if (min > i) {
             min = i;
         }
     }
     System.out.println("最大最小元素分別為："+max + " " + min);
?
     int[] bitArr = new int[max - min + 1];
     for (int i : arr) {
         int index = i - min;
         bitArr[index]++;
     }

     System.out.println("bitmap后的數組元素為：");
     for (int i : bitArr) {
         System.out.print(i+" ");
     }
     System.out.println();
?
     int index = 0;
     for (int i = 0; i < bitArr.length; i++) {
         while (bitArr[i] > 0) {
             arr[index] = i + min;
             index++;
             bitArr[i]--;
         }
     }
 }
?
 public static void main(String[] args) {
     int[] arr = { 1, 7, -3, 0, 0, 6, 6, 9, -11 };
     bitmapSort(arr);
     System.out.println("Bitmap排序后的結果：");
     for (int i : arr) {
         System.out.print(i + " ");
     }
 }
 }

位圖法存數據

???? Bit-map是用一個bit位來標記某個元素對應的Value， 而Key即是該元素。由于采用了Bit為單位來存儲數據，因此在存儲空間方面，可以大大節省。 在 8K 字節的內存空間內，如何存 unsigned short 類型數據？

一般做法：

定義一個數組： unsigned short arrNormal[4096]; 這樣做，最多只能存 4K 個 unsigned short 數據。

利用位圖法：

定義一個數組： unsigned char arrBit[4096]; 這樣做，能存 4K*8=32K 個 unsigned short 數據。

???? 寫數據元素：計算待寫入數據在 arrBit 存放的字節位置和位位置（字節 0~4095 ，位 0~7 ）

比如首先寫 1234 ，字節序： 1234/8 = 154; 比特位序： 1234 & 0b111 = 2 ，那么 1234 放在 arrBit 數組的下標為 154 處，把該字節的 2 號位（ 0~7）置為 1。

字節位置： int nBytePos = 1234/8 = 154;

位位置： int nBitPos = 1234 & 7 = 2;

// 把數組下標為 154 的 第2 個bit位置為 1

unsigned short val = 1<<nBitPos;

arrBit[nBytePos] = arrBit[nBytePos] | val;??? // 寫入 1234 得到 arrBit[154]=0b00000100

此時再寫入 1236 ，

字節位置： int nBytePos = 1236/8 = 154;

位位置： int nBitPos = 1236 & 7 = 4

// 把數組下標為 154 的 第4 個bit位置為 1

val = 1<<nBitPos;

arrBit[nBytePos] = arrBit[nBytePos] | val;??? // 再寫入 1236 得到 arrBit[154]=0b00010100

獲取插入數據后的value值為：

   1: int bytepos = data/8;

   2: int bitpos = data&7;

   3:? 

   4: bitarr[bytepos] = bitarr[bytepos]|(1<<(7-bitpos));

   5:? 

   6: int i = bitarr[bytepos];        

   7: byte[] b = toByteArray(i, 4);   //整型到字節

   8:? 

   9: System.out.println(Integer.toBinaryString(i));

   1: byte[] toByteArray(int iSource, int iArrayLen) {  

   2:     byte[] bLocalArr = new byte[iArrayLen];  

   3:     for ( int i = 0; (i < 4) && (i < iArrayLen); i++) {  

   4:         bLocalArr[i] = (byte)( iSource>>8*i & 0xFF );           

   5:     }  

   6:     return bLocalArr;  

   7: }     

具體事例

??? 結合上述代碼，我們來看一個具體的例子。假設我們要對0-7內的5個元素(4,7,2,5,3)排序（這里假設這些元素沒有重復）。那么我們就可以采用Bit-map的方法來達到排序的目的。要表示8個數，我們就只需要8個Bit（1Bytes），首先我們開辟1Byte的空間，將這些空間的所有Bit位都置為0(如下圖：)

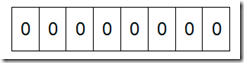
然后遍歷這5個元素，首先第一個元素是4，那么就把4對應的位置為1（可以這樣操作 p+(i/8)|(0×01<<(i%8)) 當然了這里的操作涉及到Big Endian 和 Little Endian的情況，這里默認為Big Endian ）,因為是從零開始的，所以要把第五位置為一（如下圖）：

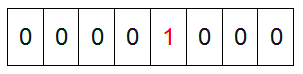
然后再處理第二個元素7，將第八位置為1,，接著再處理第三個元素，一直到最后處理完所有的元素，將相應的位置為1，這時候的內存的Bit位的狀態如下：

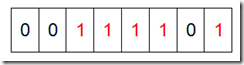
然后我們現在遍歷一遍Bit區域，將該位是一的位的編號輸出（2，3，4，5，7），這樣就達到了排序的目的。

位圖法的缺點：

1. 可讀性差。

2. 位圖存儲的元素個數雖然比一般做法多，但是存儲的元素大小受限于存儲空間的大小。

???? 位圖存儲性質：存儲的元素個數等于元素的最大值。比如， 1K 字節內存，能存儲 8K 個值大小上限為 8K 的元素。（元素值上限為 8K ，這個局限性很大！）比如，要存儲最大值為 65535 的數，就必須要 65535/8=8K 字節的內存。導致了位圖法根本不適合數組中元素差異較大的情況。{1,1000，1000000}

3. 位圖對有符號類型數據的存儲，需要 2 位來表示一個有符號元素。這會讓位圖能存儲的元素個數，元素值大小上限減半。比如 8K 字節內存空間存儲 short 類型（有符號short）數據只能存 8K*4=32K 個，元素值大小范圍為 -32K~32K 。

Big endian與little endian區別附錄：

big endian是指低地址存放最高有效字節（MSB），而little endian則是低地址存放最低有效字節（LSB）。

比如0x12345678在兩種不同字節序中的存儲順序如下所示：
Big Endian

低地址?????????????????????????????????????????????????????????? 高地址
?? ----------------------------------------->
?? +-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+
?? |???? 12???? |????? 34??? |???? 56????? |???? 78??? |
?? +-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+
Little Endian

低地址?????????????????????????????????????????????????????????? 高地址
?? ----------------------------------------->
?? +-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+
?? |???? 78???? |????? 56??? |???? 34????? |???? 12??? |
?? +-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+