?
原文:http://blog.csdn.net/ecitnet/article/details/1799444
.
(Neural Networks in Plain English)
| 因為我們沒有很好了解大腦,我們經常試圖用最新的技術作為一種模型來解釋它。在我童年的時候,我們都堅信大腦是一部電話交換機。(否 則它還能是什么呢?)我當時還看到英國著名神經學家謝林頓把大腦的工作挺有趣地比作一部電報機。更早些時候,弗羅伊德經常把大腦比作一部水力發電機,而萊 布尼茨則把它比作了一臺磨粉機。我還聽人說,古希臘人把大腦功能想象為一付彈弓。顯然,目前要來比喻大腦的話,那只可能是一臺數字電子計算機了。??????????????????????????????????????????????????????????????????? ?-John R.Searle[注1] |
曾有很長一個時期,人工神經網絡對我來說是完全神秘的東西。當然,有關它們我在文獻中已經讀過了,我也能描述它們的結構和工作機理,但我始終沒有能“啊 哈!”一聲,如同你頭腦中一個難于理解的概念有幸突然得到理解時的感覺那樣。我的頭上好象一直有個榔頭在敲著,或者像電影Animal House(中文片名為“動物屋”)中那個在痛苦地尖叫“先生,謝謝您,再給我一個啊!”的可憐家伙那樣。我無法把數學概念轉換成實際的應用。有時我甚至 想把我讀過的所有神經網絡的書的作者都抓起來,把他們縛到一棵樹上,大聲地向他們吼叫:“不要再給我數學了,快給我一點實際東西吧!”。但無需說,這是永遠不可能發生的事情。我不得不自己來填補這個空隙...由此我做了在那種條件下唯一可以做的事情。我開始干起來了。<一笑>
生物學的神經網絡-大腦
???????????? (A Biological Neural Network–The Brain)
.... 你的大腦是一塊灰色的、像奶凍一樣的東西。它并不像電腦中的CPU那樣,利用單個的處理單元來進行工作。如果你有一具新鮮地保存到福爾馬林中的尸體,用一 把鋸子小心地將它的頭骨鋸開,搬掉頭蓋骨后,你就能看到熟悉的腦組織皺紋。大腦的外層象一個大核桃那樣,全部都是起皺的[圖0左],這一層組織就稱皮層(Cortex)。如果你再小心地用手指把整個大腦從頭顱中端出來,再去拿一把外科醫生用的手術刀,將大腦切成片,那么你將看到大腦有兩層[圖0右]: 灰色的外層(這就是“灰質”一詞的來源,但沒有經過福爾馬林固定的新鮮大腦實際是粉紅色的。) 和白色的內層。灰色層只有幾毫米厚,其中緊密地壓縮著幾十億個被稱作neuron(神經細胞、神經元)的微小細胞。白色層在皮層灰質的下面,占據了皮層的 大部分空間,是由神經細胞相互之間的無數連接組成。皮層象核桃一樣起皺,這可以把一個很大的表面區域塞進到一個較小的空間里。這與光滑的皮層相比能容納更 多的神經細胞。人的大腦大約含有1OG(即100億)個這樣的微小處理單元;一只螞蟻的大腦大約也有250,OOO個。
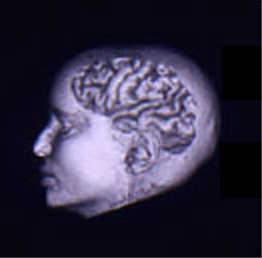 |  |
| 圖0-1 大腦半球像核桃 | 圖0-2 大腦皮層由灰質和白質組成 |
圖0? 大腦的外形和切片形狀
| 動 物 | ?神經細胞的數目(數量級) |
| ?蝸 牛 | ?10,000 (=10^4) |
| ?蜜 蜂 | ?100,000 (=10^5) |
| ?蜂 雀 | ?10,000,000 (=10^7) |
| ?老 鼠 | ?100,000,000 (=10^8) |
| ?人 類 | ??10,000,000,000 (=10^10) |
| ?大 象 | ??100,000,000,000 (=10^11) |
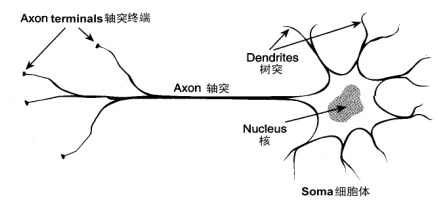 ? ? |
| 圖1神經細胞的結構 |
在人的生命的最初9個月內,這些細胞以每分鐘25,000個的驚人速度被創建出來。神經細胞和人身上任何其他類型細胞十分不同,每個神經細胞都長著一根 像電線一樣的稱為軸突(axon)的東西,它的長度有時伸展到幾厘米[譯注],用來將信號傳遞給其他的神經細胞。神經細胞的結構如圖1所 示。它由一個細胞體(soma)、一些樹突(dendrite) 、和一根可以很長的軸突組成。神經細胞體是一顆星狀球形物,里面有一個核(nucleus)。樹突由細胞體向各個方向長出,本身可有分支,是用來接收信號 的。軸突也有許多的分支。軸突通過分支的末梢(terminal)和其他神經細胞的樹突相接觸,形成所謂的突觸(Synapse,圖中未畫出),一個神經 細胞通過軸突和突觸把產生的信號送到其他的神經細胞。
| 有趣的事實 ??????? 曾經有人估算過,如果將一個人的大腦中所有神經細胞的軸突和樹突依次連接起來,并拉成一根直線,可從地球連到月亮,再從月亮返回地球。如果把地球上所有人腦的軸突和樹突連接起來,則可以伸展到離開們最近的星系! |
神經細胞利用電-化學過程交換信號。輸入信號來自另一些神經細胞。這些神經細胞的軸突末梢(也就是終端) 和本神經細胞的樹突相遇形成突觸(synapse),信號就從樹突上的突觸進入本細胞。信號在大腦中實際怎樣傳輸是一個相當復雜的過程,但就我們而言,重 要的是把它看成和現代的計算機一樣,利用一系列的0和1來進行操作。就是說,大腦的神經細胞也只有兩種狀態:興奮(fire)和不興奮(即抑制)。發射信 號的強度不變,變化的僅僅是頻率。神經細胞利用一種我們還不知道的方法,把所有從樹突上突觸進來的信號進行相加,如果全部信號的總和超過某個閥值,就會激 發神經細胞進入興奮(fire)狀態,這時就會有一個電信號通過軸突發送出去給其他神經細胞。如果信號總和沒有達到閥值,神經細胞就不會興奮起來。這樣的 解釋有點過分簡單化,但已能滿足我們的目的。
能實現無監督的學習。?有 關我們的大腦的難以置信的事實之一,就是它們能夠自己進行學習,而不需要導師的監督教導。如果一個神經細胞在一段時間內受到高頻率的刺激,則它和輸入信號 的神經細胞之間的連接強度就會按某種過程改變,使得該神經細胞下一次受到激勵時更容易興奮。這一機制是50多年以前由Donard Hebb在他寫的Organination of Behavior一書中闡述的。他寫道:
| “當神經細胞 A的一個軸突重復地或持久地激勵另一個神經細胞B后,則其中的一個或同時兩個神經細胞就會發生一種生長過程或新陳代謝式的變化,使得勵 B細胞之一的A細胞,它的效能會增加” |
?
.
(連載之二)
| ?有趣的事實 ?????? 有 一個叫 Hugo de Garis的同行,曾在一個雄心勃勃的工程中創建并訓練了一個包含1000,000,000個人工神經細胞的網絡。這個人工神經網絡被他非常巧妙地建立起 來了,它采用蜂房式自動機結構,目的就是為一機器客戶定制一個叫做CAM BrainMachine(“CAM大腦機器”) 的機器(CAM就是Cellular Automata Machine的縮寫)。此人曾自夸地宣稱這一人工網絡機器將會有一只貓的智能。許多神經網絡研究人員認為他是在“登星”了,但不幸的是,雇用他的公司在 他的夢想尚未實現之前就破產了。此人現在猶他州,是猶他州大腦工程(Utah Brain Project)的領導。時間將會告訴我們他的思想最終是否能變成實際有意義的東西。[譯注]? |
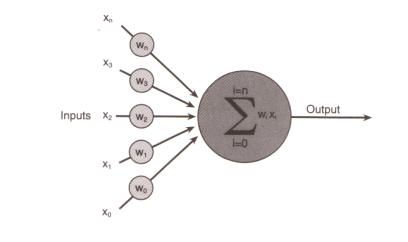
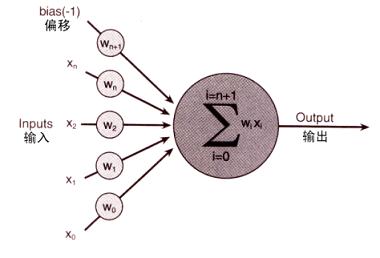
? 我想你現在可能很想知道,一個人工神經細胞究竟是一個什么樣的東西?但是,它實際上什么東西也不像; 它只是一種抽象。還是讓我們來察看一下圖2吧,這是表示一個人工神經細胞的一種形式。
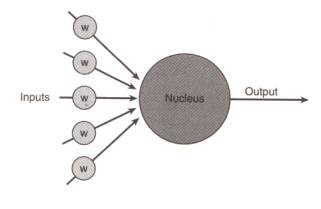
圖2 一個人工神經細胞
?如果到目前為止你對這些還沒有獲得很多感覺,那也不必擔心。竅門就是: 不要企圖去感覺它,暫時就隨波逐流地跟我一起向前走吧。在經歷本章的若干處后,你最終就會開始弄清楚它們的意義。而現在,就放松一點繼續讀下去吧。
?今后討論中,我將盡量把數學降低到絕對少量,但學習一些數學記號對下面還是很有用的。我將把數學一點一點地喂給你,在到達有關章節時向你介紹一些新概 念。我希望采用這樣的方式能使你的頭腦能更舒適地吸收所有的概念,并使你在開發神經網絡的每個階段都能看到怎樣把數學應用到工作中。現在首先讓我們來看一 看,怎樣把我在此之前告訴你的所有知識用數學方式表達出來。
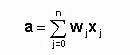
?神經網絡的各個輸入,以及為各個神經細胞的權重設置,都可以看作一個n維的向量。你在許多技術文獻中常常可以看到是以這樣的方式來引用的。?
for(int i=0; i<n; ++i)
?{
?activation += x[i] * w[i];
?}
?在進一步讀下去之前,請你一定要確切弄懂激勵函數怎樣計算。
?
?表2? 神經細胞激勵值的計算
| 輸 入 | ?權 重 | ?輸入*權重的乘積 | ?運行后總和? |
| 1 | ?0.5 | ?0.5 | ?0.5? |
| 0 | -0.2 | ?0 | ?0.5 |
| 1? | -0.3? | -0.3? | ?0.2? |
| 1? | 0.9 | ?0.9? | ?1.1? |
| 0 | 0.1? | ?0 | ?1.1 |
?
3.2? 行,我知道什么是神經細胞了,但用它來干什么呢?
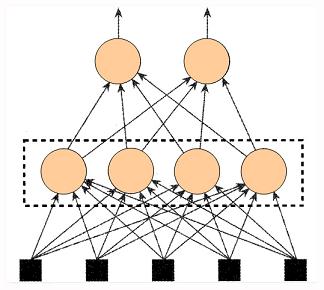
? 大腦里的生物神經細胞和其他的神經細胞是相互連接在一起的。為了創建一個人工神經網絡,人工神經細胞也要以同樣方式相互連接在一起。為此可以有許多不同 的連接方式,其中最容易理解并且也是最廣泛地使用的,就是如圖5所示那樣,把神經細胞一層一層地連結在一起。這一種類型的神經網絡就叫前饋網絡 (feedforword network)。這一名稱的由來,就是因為網絡的每一層神經細胞的輸出都向前饋送(feed)到了它們的下一層(在圖中是畫在它的上面的那一層),直到 獲得整個網絡的輸出為止。
?
圖5 一個前饋網絡
?到此我能想象你或許已對所有這些信息感到有些茫然了。我認為,在這種情況下,我能做的最好的事情,就是向你介紹一個神經網絡在現實世界中的實際應用例子,它有望使你自己的大腦神經細胞得到興奮!不錯吧?好的,下面就來了...
??? 你可能已聽到或讀到過神經網絡常常用來作模式識別。這是因為它們善于把一種輸入狀態(它所企圖識別的模式)映射到一種輸出狀態(它曾被訓練用來識別的模式)。
? 下面我們來看它是怎么完成的。我們以字符識別作為例子。設想有一個由8x8個格子組成的一塊面板。每一個格子里放了一個小燈,每個小燈都可獨立地被打開(格子變亮)或關閉(格子變黑),這樣面板就可以用來顯示十個數字符號。圖6顯示了數字“4”。

? 一旦神經網絡體系創建成功后,它必須接受訓練來認出數字 “4”。為此可用這樣一種方法來完成:先把神經網的所有權重初始化為任意值。然后給它一系列的輸入,在本例中,就是代表面板不同配置的輸入。對每一種輸入 配置,我們檢查它的輸出是什么,并調整相應的權重。如果我們送給網絡的輸入模式不是“4”, 則我們知道網絡應該輸出一個0。因此每個非“4”字符時的網絡權重應進行調節,使得它的輸出趨向于0。當代表“4”的模式輸送給網絡時,則應把權重調整到 使輸出趨向于1。
?如果你考慮一下這個網絡,你就會知道要把輸出增加到10是很容易的。然后通過訓練,就可以使網絡能識別0到9 的所有數字。但為什么我們到此停止呢?我們還可以進一步增加輸出,使網絡能識別字母表中的全部字符。這本質上就是手寫體識別的工作原理。對每個字符,網絡 都需要接受許多訓練,使它認識此文字的各種不同的版本。到最后,網絡不單能認識已經訓練的筆跡,還顯示了它有顯著的歸納和推廣能力。也就是說,如果所寫文 字換了一種筆跡,它和訓練集中所有字跡都略有不同,網絡仍然有很大幾率來認出它。正是這種歸納推廣能力,使得神經網絡已經成為能夠用于無數應用的一種無價 的工具,從人臉識別、醫學診斷,直到跑馬賽的預測,另外還有電腦游戲中的bot(作為游戲角色的機器人)的導航,或者硬件的robot(真正的機器人)的 導航。
???? 這種類型的訓練稱作有監督的學習(supervised learnig),用來訓練的數據稱為訓練集(training set)。調整權重可以采用許多不同的方法。對本類問題最常用的方法就是反向傳播(backpropagation,簡稱backprop或BP)方法。 有關反向傳播問題,我將會在本書的后面,當你已能訓練神經網絡來識別鼠標走勢時,再來進行討論。在本章剩余部分我將集中注意力來考察另外的一種訓練方式, 即根本不需要任何導師來監督的訓練,或稱無監督學習(unsupervised learnig)。
???? 這樣我已向你介紹了一些基本的知識,現在讓我們來考察一些有趣的東西,并向你介紹第一個代碼工程。

圖7 運行中的演示程序。
?
??????? 怎么樣,很酷吧?
| 提示(重要) ???? ?如果你跳過前面的一些章節來到這里,而你又不了解怎樣使用遺? 傳算法,則在進一步閱讀下面的內容之前,你應回到前面去補讀一下有關遺傳算法的內容。 |
?
?????? 首先讓我解釋人工神經網絡(ANN)的體系結構。我們需要決定輸入的數目、輸出的數目、還有隱藏層和每個隱藏層中隱藏單元的數目。
??????? 那么,人工神經網絡怎樣控制掃雷機的行動呢?很好!我們把掃雷機想象成和坦克車一樣,通過左右2個能轉動的履帶式輪軌(track)來行動的。見圖案9.8。
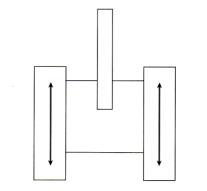
? 掃雷機向前行進的速度,以及向左、向右轉彎的角度,都是通過改變2個履帶輪的相對速度來實現的。因此,神經網絡需要2個輸入,1個是左側履帶輪的速度,另一個是右側履帶輪的速度。
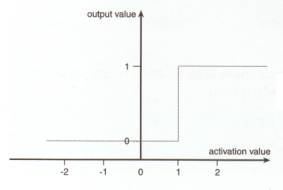
? 啊,但是...,我聽見你在嘀咕了。如果網絡只能輸出一個1或一個0,我們怎么能控制車軌移動的快慢呢? 你是對的;如果利用以前描述的階躍函數來決定輸出,我們就根本無法控制掃雷機實際移動。幸好,我有一套戲法,讓我卷起袖子來,把激勵函數的輸出由階躍式改 變成為在0-1之間連續變化的形式,這樣就可以供掃雷機神經細胞使用了。為此,有幾種函數都能做到這樣,我們使用的是一個被稱為邏輯斯蒂S形函數 (logistic sigmoid function)[譯注1]。該函數所實現的功能,本質上說,就是把神經細胞原有的階躍式輸出曲線鈍化為一光滑曲線,后者繞y軸0.5處點對稱[譯注 2],如圖9所示。
?
[譯注1] logistic有’計算的’或’符號邏輯的’等意思在內,和’邏輯的(logic)’意義不同。
[譯注2] 點對稱圖形繞對稱點轉180度后能與原圖重合。若f(x)以原點為點對稱,則有f(-x)=-f(x)
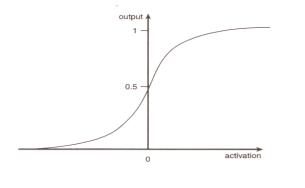
圖9 S形曲線。

?
注:“S型”的英文原名Sigmoid 或Sigmoidal 原來是根據希臘字“Sigma”得來的,但非常巧它也可以說成是曲線的一種形狀。?
?
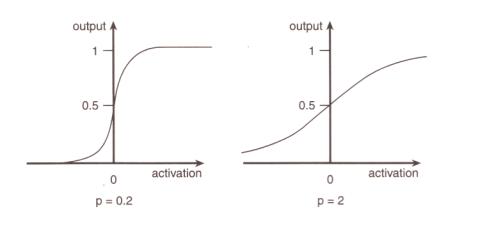
圖7。10? 不同的S形響應曲線。
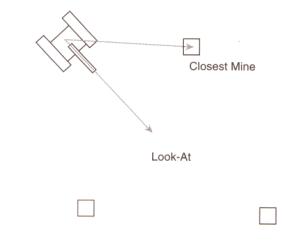
? 上面我們已經把輸出安排好了,現在我們來考慮輸入,確定網絡需要什么樣的輸入?為此,我們必須想象一下掃雷機的具體細節:需要什么樣的信息才能使它朝地雷前進?你可能想到的第一個輸入信息清單是:
- 掃雷機的位置(x1,y1)
- 與掃雷機最靠近的地雷的位置(x2,y2)
- 代表掃雷機前進方向的向量(x3,y3)
? 只要作少量的額外考慮,就能夠把輸入的個數減少為4,這就是圖11中所畫出的兩個向量的4個參數。
??????? 把神經網絡的所有輸入進行規范化是一種好想法。這里的意思并不是說每個輸入都要改變大小使它們都在0~1間,而是說每一個輸入應該受到同等重視。例如,拿 我們已經討論過的掃雷機輸入為例。瞄準向量或視線向量(look-at vector)總是一個規范化向量,即長度等于1,分量x和y都在0~1間。但從掃雷機到達其最近地雷的向量就可能很大,其中的一個分量甚至有可能和窗體 的寬度或高度一樣大。如果這個數據以它的原始狀態輸入到網絡,網絡對有較大值的輸入將顯得更靈敏,由此就會使網絡性能變差。因此,在信息輸入到神經網絡中 去之前,數據應預先定比(scaled)和標準化(standardized),使它們大小相似(similar)。在本特例中,由掃雷機引到與其最接近 地雷的向量需要進行規范化(normalized)。這樣可以使掃雷機的性能得到改良。
?
?
圖11 選擇輸入。
| ?小技巧: ??? 有時,你把輸入數據重新換算(rescale)一下,使它以0點為中心,就能從你的神經網絡獲得最好的性能。這一小竅門在你設計網絡時永遠值得一試。但我在掃雷機工程中沒有采用這一方法,這是因為我想使用一種更直覺的方法。 |
? 到此我們已把輸入、輸出神經細胞的數目和種類確定下來了,下一步是確定隱藏層的數目,并確定每個隱藏層中神經細胞必須有多少?但遺憾的是,還沒有一種確 切的規則可用來計算這些。它們的開發又需要憑個人的“感覺”了。某些書上和文章中確實給過一些提綱性的東西,告訴你如何去決定隱藏神經細胞個數,但業內專 家們的一致看法是:你只能把任何建議當作不可全信的東西,主要還要靠自己的不斷嘗試和失敗中獲得經驗。但你通常會發現,你所遇到的大多數問題都只要用一個 隱藏層就能解決。所以,本領的高低就在于如何為這一隱藏層確定最合適的神經細胞數目了。顯然,個數是愈少愈好,因為我前面已經提及,數目少的神經細胞能夠 造就快速的網絡。通常,為了確定出一個最優總數,我總是在隱藏層中采用不同數目的神經細胞來進行試驗。我在本章所編寫的神經網絡工程的.
.
(連載之四)
? 在CNeuralNet.h 文件中,我們定義了人工神經細胞的結構、定義了人工神經細胞的層的結構、以及人工神經網絡本身的結構。首先我們來考察人工神經細胞的結構。
{
???? // 進入神經細胞的輸入個數
???? int m_NumInputs;
????
???? // 為每一輸入提供的權重
???? vector<double> m_vecWeight;
????
???? //構造函數
???? SNeuron(int NumInputs);
? };
?(
???? // 我們要為偏移值也附加一個權重,因此輸入數目上要 +1
???? for (int i=0; i<NumInputs+1; ++i)
???? {
???????? // 把權重初始化為任意的值
??????? ?m_vecWeight.push_back(RandomClamped());
???? }
?}
? 由上可以看出,構造函數把送進神經細胞的輸入數目NumInputs作為一個變元,并為每個輸入創建一個隨機的權重。所有權重值在-1和1之間。
??????? 這是什么? 我聽見你在說。這里多出了一個權重!不 錯,我很高興看到你能注意到這一點,因為這一個附加的權重十分重要。但要解釋它為什么在那里,我必須更多地介紹一些數學知識。回憶一下你就能記得,激勵值 是所有輸入*權重的乘積的總和,而神經細胞的輸出值取決于這個激勵值是否超過某個閥值(t)。這可以用如下的方程來表示:
 ?
??神經細胞層SNeuronLayer的結構很簡單;它定義了一個如圖13中所示的由虛線包圍的神經細胞SNeuron所組成的層。?
?
{
?? // 本層使用的神經細胞數目
? int???????????????? m_NumNeurons;
?
???? ?// 神經細胞的層
? vector<SNeuron>?? m_vecNeurons;
?
? SNeuronLayer(int NumNeurons, int NumInputsPerNeuron);
};
{
private:
??? int???????? ??? ???m_NumInputs;
??? vector<SNeuronLayer> ?m_vecLayers;
???? void ???CreateNet();
?
??? ?// 從神經網絡得到(讀出)權重
???? vector<double> ? GetWeights()const;
?
??? // 返回網絡的權重的總數
??? int GetNumberOfWeights()const;
??? void PutWeights(vector<double> &weights);
??????? 這一函數所做的工作與函數GetWeights所做的正好相反。當遺傳算法執行完一代時,新一代的權重必須重新插入神經網絡。為我們完成這一任務的是PutWeight方法。
???
???? // S形響應曲線
??? inline double Sigmoid(double activation, double response);
?
??? ?當已知一個神經細胞的所有輸入*重量的乘積之和時,這一方法將它送入到S形的激勵函數。
?
???? // 根據一組輸入,來計算輸出
???? vector<double> Update(vector<double> &inputs);
void CNeuralNet::CreateNet()
{
?? ?// 創建網絡的各個層
??? if (m_NumHiddenLayers > 0)
???? ?{
????? //創建第一個隱藏層[譯注]
???? ?m_vecLayers.push_back(SNeuronLayer(m_NeuronsPerHiddenLyr,
?????????????????????????????????????????? m_NumInputs));
?
??? ?for( int i=O; i<m_NumHiddenLayers-l; ++i)
??? ?{
??????? m_vecLayers.push_back(SNeuronLayer(m_NeuronsPerHiddenLyr,
????????????????????????????????????????????????? m_NeuronsPerHiddenLyr));
????? }
?
[譯注]如果允許有多個隱藏層,則由接著for循環即能創建其余的隱藏層。
????? // 創建輸出層
????? m_vecLayers.push_back(SNeuronLayer(m_NumOutput,m_NeuronsPerHiddenLyr));
?? }
?? {
????? ?// 創建輸出層
?????? ?m_vecLayers.push_back(SNeuronLayer(m_NumOutputs, m_NumInputs));
?? }
}
4.4.3.2? CNeuralNet::Update(神經網絡的更新方法)
{
??? ?// 保存從每一層產生的輸出
??? ?vector<double> outputs;
??? ?if (inputs.size() != m_NumInputs)
????? {
??????? ? // 如果不正確,就返回一個空向量
????????? return outputs;
???? ?}
?
???? // 對每一層,...
???? for (int i=0; i<m_NumHiddenLayers+1; ++i)
???? {
?????? if (i>O)
???????? {
??????????? inputs = outputs;
???????? }
?? ?outputs.clear();
?
?? ?cWeight = 0;
?
?? ?// 對每個神經細胞,求輸入*對應權重乘積之總和。并將總和拋給S形函數,以計算輸出
?? for (int j=0; j<m_vecLayers[i].m_NumNeurons; ++j)
??????? {
????????? double netinput = 0;
????
????????? int NumInputs = m_vecLayers[i].m_vecNeurons[j].m_NumInputs;
????
???????? // 對每一個權重
???????? for (int k=O; k<NumInputs-l; ++k)
???????? {
??????????? // 計算權重*輸入的乘積的總和。
??????????? netinput += m_vecLayers[i].m_vecNeurons[j].m_vecWeight[k] *
???? ?? ????? inputs[cWeight++];
???????? }
????
??????? // 加入偏移值
??????? netinput += m_vecLayers[i].m_vecNeurons[j].m_vecWeight[NumInputs-1] *
????????????????? ??CParams::dBias;
???? // 激勵總值首先要通過S形函數的過濾,才能得到輸出
outputs.push_back(Sigmoid(netinput,CParams::dActivationResponse)); cWeight = 0:
??? }
? }
}
.
(連載之五)
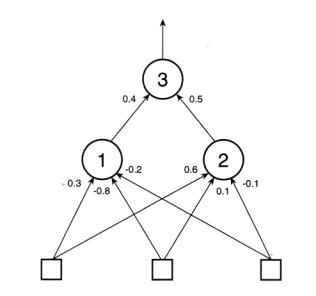
?在本書的開始幾章中,你已經看到過怎樣用各種各樣的方法為遺傳算法編碼。但當時我并沒有向你介紹過
一個用實數編碼的具體例子,因為我知道我要留在這里向你介紹。我曾經講到,為了設計一個前饋型神經網絡,
編碼是很容易的。我們從左到右讀每一層神經細胞的權重,讀完第一個隱藏層,再向上讀它的下一層,把所讀
到的數據依次保存到一個向量中,這樣就實現了網絡的編碼。因此,如果我們有圖14所示的網絡,則它的權重
編碼向量將為:
個權重,否則你肯定無法獲得你所需要的結果。
4.6? 遺傳算法(The Genetic Algorithm)
??????? 到此,所有的權重已經象二進制編碼的基因組那樣,形成了一個串,我們就可以象本書早先討論過的那樣
來應用遺傳算法了。遺傳算法(GA)是在掃雷機已被允許按照用戶指定的幀數(為了某種緣故, 我下面更喜歡
將幀數稱作滴答數,英文是ticks)運轉后執行的。你可以在ini文件中找到這個滴答數(iNumTicks)的設置。
下面是基因組結構體的代碼。這些對于你應該是十分面熟的東西了。
?
Struct SGenome
?{
? vector <double> vecWeights;
?
? double ?dFitness;
?
? SGenome():dFitness(0) {}
?
? SGenome(vector <double> w, double f):vecWeights(w),dFitness(f){}
?
? //重載'<'的排序方法
????? friend bool? operator<(const SGenome& lhs, const SGenome& rhs)
???????? {
???? ????? return (lhs.dFitness < rhs.dFitness);
???????? }
?};
操作。但突變操作則稍微有些不同,這里的權重值是用一個最大值為dMaxPerturbation的隨機數來搔擾的。這一
參數dMaxPerturbation在ini文件中已作了聲明。另外,作為浮點數遺傳算法,突變率也被設定得更高些。在本工
程中,它被設成為0.1。
{
? // 遍歷權重向量,按突變率將每一個權重進行突變
? for (int i=0; i<chromo.size(); ++i)
? {
???? // 我們要騷擾這個權重嗎?
???? if (RandFloat() < m_dMutationRate)
???? {
?????? // 為權重增加或減小一個小的數量
?????? chromo[i] += (RandomClamped() * CParams::dMaxPerturbatlon);
???? }
? }
}
就能給你留下許多余地,可讓你利用以前學到的技術來改進它。就象大多數別的工程一樣,v1.O版只用輪盤賭
方式選精英,并采用單點式雜交。
?當程序運行時,權重可以被演化成為任意的大小,它們不受任何形式的限制。?
4.7? 掃雷機類(The CMinesweeper Class)
?這一個類用來定義一個掃雷機。就象上一章描述的登月艇類一樣,掃雷機類中有一個包含了掃雷機位置、
速度、以及如何轉換方向等數據的紀錄。類中還包含掃雷機的視線向量(look-at vector);它的2個分量被用
來作為神經網絡的2個輸入。這是一個規范化的向量,它是在每一幀中根據掃雷機本身的轉動角度計算出來的,
它指示了掃雷機當前是朝著哪一個方向,如圖11所示。
{
private:
???? // 掃雷機的神經網絡
????? CNeuralNet??????? m_ItsBrain;
???? SVector2D???????? m_vPosition;
???? // 掃雷機面對的方向
???? SVector2D????????? m_vLookAt;
???? double ???? m_dRotation;
???? double???????? m_lTrack,
?????????? ???????? m_rTrack;
???? 這些就是用來決定掃雷機的移動速率和轉動角度的數值。
???? double ?? m_dFitness;
???? double????? m_dScale;
???? int?????? m_iClosestMine;
??? 而m_iClosestMine就是代表最靠近掃雷機的那個地雷在該向量中的位置的下標。
????bool Update(vector<SVector2D> &mines);
????void? WorldTransform(vector<SPoint> &sweeper);
??? // 返回一個向量到最鄰近的地雷
??? 5Vector2D GetClosestMine(vector<SVector2D> &objects);
??? int??????? CheckForMine(vector<SVector2D> &mines, double size);
????
??? void?????? Reset();
??? SVector2D? Position()const { return m_vPosition; }
??? void?????? IncrementFitness(double val) { m_dFitness += val; }
??? double???? Fitness()const { return m_dFitness; }
??? void?????? PutWeights(vector<double> &w) { m_ItsBrain.PutWeights(w); }
??? int??????? GetNumberOfWeights()const
????????????????????????????? { return m_ItsBrain.GetNumberOfWeights(); }
};
4.7.1 The CMinesweeper::Update Function(掃雷機更新函數)
都要被調用,以更新掃雷機神經網絡。讓我們考察這函數的肚子里有些什么貨色:
???? //這一向量用來存放神經網絡所有的輸入
???? vector<double> inputs;
???? SVector2D vClosestMine = GetClosestMine(mines);
???? Vec2DNormalize(vClosestMine);
的長度等于1。)但掃雷機的視線向量(look-at vector)這時不需要再作規范化,因為它的長度已經等于1了。
由于兩個向量都有效地化成了同樣的大小范圍,我們就可以認為輸入已經是標準化了,這我前面已講過了。
?
???? //加入掃雷機->最近地雷之間的向量
???? Inputs.push_back(vClosestMine.x);
???? Inputs.push_back(vCIosestMine.y);
???? Inputs.push_back(m_vLookAt.x);
???? Inputs.push_back(m_vLookAt.y);
???? vector<double> output = m_ItsBrain.Update(inputs);
用這些信息來更新掃雷機網絡,并返回一個std::vector向量作為輸出。
???? if (output.size() < CParams::iNumOutputs)
????? {
???????? return false;
????? }
???? m_lTrack = output[0];
???? m_rTrack = output[1];
到掃雷機左、右履帶輪軌上的力。
???? double RotForce = m_lTrack - m_rTrack;
???? Clamp(RotForce, -CParams::dMaxTurnRate, CParams::dMaxTurnRate);
??
??? ?m_dSpeed = (m_lTrack + m_rTrack);
?掃雷機車的轉動力是利用施加到它左、右輪軌上的力之差來計算的。并規定,施加到左軌道上的力減去施
加到右軌道上的力,就得到掃雷機車輛的轉動力。然后就把此力施加給掃雷機車,使它實行不超過ini文件所規
定的最大轉動率的轉動。而掃雷機車的行進速度不過就是它的左側輪軌速度與它的右側輪軌速度的和。既然我
們知道了掃雷機的轉動力和速度,它的位置和偏轉角度也就都能更新了。
???? m_dRotation += RotForce;
????
???? // 更新視線角度
???? m_vLookAt.x = -sin(m_dRotation);
???? m_vLookAt.y = cos(m_dRotation);
???? m_vPosition += (m_vLookAt* m_dSpeed);
???? If (m_vPosition.x > CParams::WindowWidth) m_vPosition.x = 0;
???? If (m_vPosition.x < 0) m_vPosition.x = CParams::WindowWidth;
???? If (m_vPosition.y > CParams::WindowHeight) m_vPosition.y = 0;
???? If (m_vPosition.y < D) m_vPosition.y = CParams::WindowHeight;
?
? 為了使事情盡可能簡單,我已讓掃雷機在碰到窗體邊框時就環繞折回(wrap)。采用這種方法程序就不再需
要做任何碰撞-響應方面的工作。環繞一塊空地打轉對我們人來說是一樁非常不可思議的動作,但對掃雷機,這
就像池塘中的鴨子。
?}
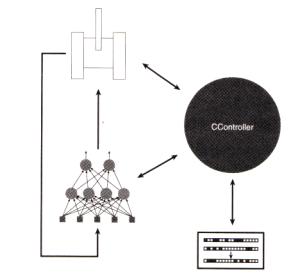
?CController類是和一切都有聯系的類。圖15指出了其他的各個類和CController類的關系。
?下面就是這個類的定義:
?
?class CController
?{
?private:
???? // 基因組群體的動態存儲器(一個向量)
????? vector<SGenome> ??m_vecThePopulation;
?
????? 圖15? minesweeper工程的程序流程圖
??? // 保存掃雷機的向量
??? vector<CMinesweeper> ?m_vecSweepers;
????
??? // 保存地雷的向量
??? vector<SVector2D> ??m_vecMines;
? ? CGenAIg* ???????? m_pGA;
?
? ? int ????????????? m_NumSweepers;
?
? ? int ????????????? m_NumMines;
? ? int ????????????? m_NumWeightsInNN;
??? vector<SPoint> ???m_SweeperVB;
? ? vector<SPoint> ???m_MineVB;
? ? vector<double> ???m_vecAvFitness;
?
? ? // 存放每一代的最高適應性分
??? vector<double> ???m_vecBestFitness;
? ? HPEN ???????????? m_RedPen;
? ? HPEN ???????????? m_BluePen;
? ? HPEN ???????????? m_GreenPen;
? ? HPEN ???????????? m_OldPen;
? ? HWND ???????????? m_hwndMain;
??? bool ???????????? m_bFastRender;
???
??? // 每一代的幀數(滴答數)
??? int ????????????? m_iTicks;
??? int ????????????? m_iGenerations;
??? int ????????????? cxClient,cyClient;
??? void????????????? PlotStats(HDC surface);
?????????? SVector2D??????? vPos);
??? bool ??FastRender() { return m_bFastRender; }
??? void ??FastRender(bool arg){ m_bFastRender = arg; }
??? void ??FastRenderToggle() { m_bFastRender = !m_bFastRender; }
};
統計神經網絡中所使用的權重的總數,然后此數字即被利用來初始化遺傳算法類的一個實例。
從遺傳算法對象中隨機提取染色體(權重)并(利用細心的腦外科手術)插入到掃雷機的經網絡中。
創建了大量的地雷并被隨機地散播到各地。
為繪圖函數創建了所有需要用到的GDI畫筆。
為掃雷機和地雷的形狀創建了頂點緩沖區。
?
?所有的一切現都已完成初始化,由此Update方法就能在每一幀中被調用來對掃雷機進行演化。
?
?
4.8.1? CController::Update Method(控制器的更新方法)
的 前一半通過對所有掃雷機進行循環,如發現某一掃雷機找到了地雷,就update該掃雷機的適應性分數。由于m_vecThePopulation包含了所 有基因組的拷貝,相關的適應性分數也要在這時進行調整。如果為完成一個代(generation)所需要的幀數均已通過,本方法就執行一個遺傳算法的時代 (epoch)來產生新一代的權重。這些
權重被用來代替掃雷機神經網絡中原有的舊的權重,使掃雷機的每一個參數被重新設置,從而為進入新一generation做好準備。
???
?bool CController::Update()
?{
???? // 掃雷機運行總數為CParams::iNumTicks次的循環。在此循環周期中,掃雷機的神經網絡
???? // 不斷利用它周圍特有的環境信息進行更新。而從神經網絡得到的輸出,使掃雷機實現所需的
???? // 動作。如果掃雷機遇見了一個地雷,則它的適應性將相應地被更新,且同樣地更新了它對應
???? // 基因組的適應性。
???? if (m_iTicks++ < CParams::iNumTicks)
?????? {
??????? for (int i=O; i<m_NumSweepers; ++i)
??????? {
??????? //更新神經網絡和位置
????????? if (!m_vecSweepers[i].Update(m_vecMines))
?????????? {
??????????? //處理神經網絡時出現了錯誤,顯示錯誤后退出
???????????? MessageBox(m_hwndMain, 'Wrong amount of NN inputs!",
????????????? ?"Error", MB_OK);
?
???????????? return false;
????????? ?}
???????? int GrabHit = m_vecSweepers[i].CheckForMine(m_vecMines,
???????????????????????????????????????????????? ??? CParams::dMineScale);
????????? {
??????????? // 掃雷機已找到了地雷,所以要增加它的適應性分數
??????????? m_vecSweepers[i].IncrementFitness();
??????????? m_vecMines[GrabHit] = SVector2D(RandFloat() * cxClient,
?????????????????????????????????????? ?? RandFloat() * cyClient);
????????? }
??????? m-vecThePopulation[i].dFitness = m_vecSweepers[i].Fitness();
????? }
?? }
?? // 一個代已被完成了。
?? // 進入運行遺傳算法并用新的神經網絡更新掃雷機的時期
?? else
??? {
???? // 更新用在我們狀態窗口中狀態
???? m_vecAvFitness.push_back(m_pGA->AverageFitness());
???? m_vecBestFitness.push_back(m_pGA->BestFitness());
???? ++m_iGenerations;
?
???? // 將幀計數器復位
???? m_iTicks = 0;
???? m-vecThePopulation = m_pGA->Epoch(m_vecThePopulation);
???? // 并將它們的位置進行復位,等
???? for(int i=O; i<m_NumSweepers; ++i)
????? {m_vecSweepers[i].m_ItsBrain.PutWeights(m_vecThePopulation[i].vecWeights);
????? }
??? }
? returen true;
}
?????? 并根據情況增加掃雷機適應值的得分。
???? 2.從掃雷機神經網絡提取權重向量。
???? 3.用遺傳算法去演化出一個新的網絡權重群體。
???? 4.把新的權重插入到掃雷機神經網絡。
? 5.轉到第1步進行重復,直到獲得理想性能時為止。
?
?最后,表3列出了Smart Sweepers工程 v1.0版所有缺省參數的設置值。
| 神經網絡 | |
| 參???? 數 | 設 置 值 |
| 輸入數目 | 4 |
| 輸出數目 | 2 |
| 隱藏層數目 | 1 |
| 隱藏層神經元數目 | 10 |
| 激勵響應 | 1 |
| 遺 傳 算 法 | |
| 參?? 數 | 設 置 值 |
| 群體大小 | 30 |
| 選擇類型 | 旋轉輪 |
| 雜交類型 | 單點 |
| 雜交率 | 0.7 |
| 突變率 | 0.1 |
| 精英設置(on/off) | On |
| 精英數目(N/copies) | 4/1 |
| 總 體 特 性 | |
| 參?? 數 | 設 置 值 |
| 每時代的幀數 | 2000 |
4.9? 運行此程序 (Running the Program)
??? 當你運行程序時,“F”鍵用來切換2種不同的顯示狀態,一種是顯示掃雷機怎樣學習尋找地雷,一種是
示在運行期中產生的最優的與平均的適當性分數的統計圖表。?當顯示圖表時,程序將會加速運行。
.
(連載之六)
盡管掃雷機學習尋找地雷的本領十分不錯,這里我仍有兩件事情要告訴你,它們能進一步改進掃雷機的性能。
首先,單點crossover算子留下了許多可改進的余地。按照它的規定,算子是沿著基因組長度任意地方切開的,這樣常有可能使個別神經細胞的基因組在權重的中間被一刀兩段地分開。
里,雜交算子可以沿向量長度的任意一處切開,這樣,就會有極大幾率在某個神經細胞(如第二個)的權重中
間斷開,也就是說,在權重0.6和-0.1之間某處切開。這可能不會是我們想要的,因為,如果我們把神經細胞作
為一個完整的單元來看待,則它在此以前所獲得的任何改良就要被騷擾了。事實上,這樣的雜交操作有可能非
常非常象斷裂性突變(disruptive mutation)操作所起的作用。
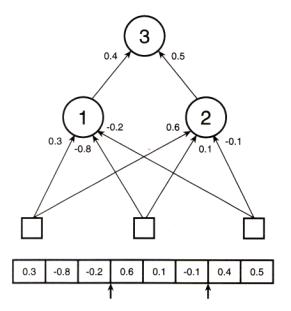 ?
?就是在第3、4或第6、7的兩個基因之間切開,如小箭頭所示。 為了實現這一算法,我已在CNeuralNet類中補
充了另一個切割方法: CalculateSplitPoints。這一方法創建了一個用于保存所有網絡權重邊界的矢量,它的代
碼如下:
{
?? vector<int> SplitPoints;
?
?? int WeightCounter = 0;
?
?? // 對每一層
?? for (int i=O; i<m_NumHiddenLayers + 1; ++i)
??? {
???? // 對每一個神經細胞
???? for (int j=O; j<m_vecLayers[i].m_NumNeurons; ++j)
? {
??????? // 對每一個權重
??????? for (int k=O; k<m_vecLayers[i].m_vecNeurons[j].m_NumInputs; ++k)
???????? {
??????????? ++WeightCounter;
???????? }
????? }
?? }
}
在一個名叫m_vecSplitPoints的std::vector向量中。然后遺傳算法就利用這些斷裂點來實現兩點雜交操作,其代
碼如下:
??????????????????????????????? ?? const vector<double>? &dad,
??????????????????????????????? ?? vector<double>???????? &babyl,
??????????????????????????????? ?? vector<double>???????? &baby2)
{
?? // 如果超過了雜交率,就不再進行雜交,把2個上代作為2個子代輸出
?? // 如果2個上輩相同,也把它們作為2個下輩輸出
?? if ( (RandFloat() > m_dCrossoverRate) || (mum == dad))
???? {
????? baby1 = mum;
????? baby2 = dad;
???? }
?? int index1 = RandInt(0, m_vecSplitPoints.size()-2);
?? int index2 = RandInt(Index1, m_vecSplitPoints.size()-1);
?? int cp2 = m_vecSplitPoints[Index2];
?
?for (int i=0; i<mum.size(); ++i)
?? {
???? if ( (i<cp1) || (i>=cp2) )
?????? {
?????????? // 如果在雜交點外,保持原來的基因
?????????? babyl.push_back(mum[i]);
?????????? baby2.push_back(dad[i]);
?????? }
?????? {
?????????? // 把中間段進行交換
?????????? baby1.push_back(dad[1]);
?????????? baby2.push_back(mum[1]);
?????? }
?? }
}
一點分裂基因組,能得到更好的結果。
網絡使用了4個輸入參數: 2個用于表示掃雷機視線方向的向量,另外2個用來指示掃雷機與其最靠近的地雷的方
向的向量。然而,有一種辦法,可以把這些參數的個數減少到只剩下一個。
向右轉動多大的一個角度這一簡單的信息就夠了(如果你已經考慮到了這一點,那我在這里要順便向您道賀了)。
由于我們已經計算了掃雷機的視線向量和從它到最鄰近地雷的向量,再來計算它們之間的角度(θ)應是一件極為
簡單的事情 – 這就是這兩個向量的點積,這我們在第6章“使登陸月球容易一點”中已討論過。見圖17。
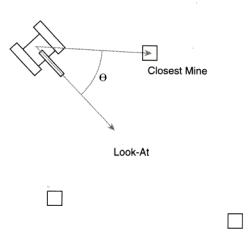
量函數返回一個向量相對于另一個向量的正負號。該函數的原型如下所示:
按順時針方向轉的,則函數返回 +1;如果v1至v2是按逆時針方向轉,則函數返回 -1。
把點積和Vec2Dsign二者聯合起來,就能把輸入的精華提純出來,使網絡只需接受一個輸入就行了。下面
就是新的CMinesweeper::Update函數有關段落的代碼形式:
?
???? // 計算到最鄰近地雷的向量
???? SVector2D vClosestMine = GetClosestMine(mines);
? Vec2DNormalize(vClosestMine);
?
?// 計算掃雷機視線向量和它到最鄰近地雷的向量的點積。它給出了我們要面對
?// 最鄰近地雷所需轉動的角度
???? double dot = Vec2DDot(m_vLookAt, vClosestMine);
???? int sign = Vec2DSign(m_vLookAt, vClosestMine);
????
? 運行一下光盤Chapter7/Smart Sweepers v1.1目錄下的可執行程序executable,你就知道經過以上2個改
進,能為演化過程提速多少。
? 需要注意的一樁重要事情是,帶有4個輸入的網絡要花很長時間進行演化,因為它必須在各輸入數據之間找
出更多的關系才能確定它應如何行動。事實上,網絡實際就是在學習怎么做點積并確定它的正負極性。因此,當
你設計自己的網絡時,你應仔細權衡一下,是由你自己預先來計算許多輸入數據好呢(它將使CPU負擔增加,但
導致進化時間加快)還是讓網絡來找輸入數據之間的復雜關系好(它將使演化時間變長,但能使CPU減少緊張)?
?我希望你已享受到了你第一次攻入神經網絡這一奇妙世界的快樂。我打賭你一定在為如此簡單就能使用它
們而感到驚訝吧,對嗎?我想我是猜對了。
? 在下面幾章里我將要向你介紹更多的知識,告訴你一些新的訓練手段和演繹神經網絡結構的更多的方法。
但首先請你利用本章下面的提示去玩一下游戲是有意義的。
1。 在v1.0中,不用look-at向量作為輸入,而改用旋轉角度θ作為輸入,由此就可以使網絡的輸入個數減少
成為1個。請問這對神經網絡的演化有什么影響?你對此的看法怎樣?
2。 試以掃雷機的位置(x1,y1)、和掃雷機最接近的地雷的位置(x2,y2)、以及掃雷機前進方向的向量
(x3,y3)等6個參數作為輸入,來設計一個神經網絡,使它仍然能夠演化去尋找地雷。
3。 改變激勵函數的響應。試用O.1 - O.3 之間的低端值,它將產生和階躍函數非常相像的一種激勵函數。
然后再試用高端值,它將給出較為平坦的響應曲線。考察這些改變對演化進程具有什么影響?
4。 改變神經網絡的適應性函數,使得掃雷機不是去掃除地雷,而是要演化它,使它能避開地雷。
5。 理一理清楚有關遺傳算法的各種不同設置和運算中使你感到模糊的東西!
6。 加入其他的對象類型,比如人。給出一個新環境來演化掃雷機,使它能避開人,但照樣能掃除地雷。
(這可能沒有你想象那么容易!)
神經網絡編程入門
Posted on 2011-03-07 22:30 蒼梧 閱讀(48399) 評論(22) 編輯 收藏本文主要內容包括: (1) 介紹神經網絡基本原理,(2)AForge.NET實現前向神經網絡的方法,(3) Matlab實現前向神經網絡的方法 。
?
第0節、引例?
?????? 本文以Fisher的Iris數據集作為神經網絡程序的測試數據集。Iris數據集可以在http://en.wikipedia.org/wiki/Iris_flower_data_set? 找到。這里簡要介紹一下Iris數據集:
有一批Iris花,已知這批Iris花可分為3個品種,現需要對其進行分類。不同品種的Iris花的花萼長度、花萼寬度、花瓣長度、花瓣寬度會有差異。我們現有一批已知品種的Iris花的花萼長度、花萼寬度、花瓣長度、花瓣寬度的數據。
一種解決方法是用已有的數據訓練一個神經網絡用作分類器。
如果你只想用C#或Matlab快速實現神經網絡來解決你手頭上的問題,或者已經了解神經網絡基本原理,請直接跳到第二節——神經網絡實現。
?
第一節、神經網絡基本原理?
1. 人工神經元(Artificial Neuron )模型?
?????? 人工神經元是神經網絡的基本元素,其原理可以用下圖表示:

圖1. 人工神經元模型
?
?????? 圖中x1~xn是從其他神經元傳來的輸入信號,wij表示表示從神經元j到神經元i的連接權值,θ表示一個閾值 ( threshold ),或稱為偏置( bias )。則神經元i的輸出與輸入的關系表示為:
?

圖中yi表示神經元i的輸出,函數f稱為激活函數 ( Activation Function )或轉移函數 ( Transfer Function ) ,net稱為凈激活(net activation)。若將閾值看成是神經元i的一個輸入x0的權重wi0,則上面的式子可以簡化為:
?

若用X表示輸入向量,用W表示權重向量,即:
X = [ x0 , x1 , x2 , ....... , xn ]
 ?
?
則神經元的輸出可以表示為向量相乘的形式:
?
?
?????? 若神經元的凈激活net為正,稱該神經元處于激活狀態或興奮狀態(fire),若凈激活net為負,則稱神經元處于抑制狀態。
?????? 圖1中的這種“閾值加權和”的神經元模型稱為M-P模型 ( McCulloch-Pitts Model ),也稱為神經網絡的一個處理單元( PE, Processing Element )。
?
2. 常用激活函數?
?????? 激活函數的選擇是構建神經網絡過程中的重要環節,下面簡要介紹常用的激活函數。
(1) 線性函數( Liner Function )
?
(2) 斜面函數( Ramp Function )
?
(3) 閾值函數( Threshold Function )
?
?
?
?????? 以上3個激活函數都屬于線性函數,下面介紹兩個常用的非線性激活函數。
(4) S形函數( Sigmoid Function )

該函數的導函數:

(5) 雙極S形函數?

該函數的導函數:

S形函數與雙極S形函數的圖像如下:

圖3. S形函數與雙極S形函數圖像
雙極S形函數與S形函數主要區別在于函數的值域,雙極S形函數值域是(-1,1),而S形函數值域是(0,1)。
由于S形函數與雙極S形函數都是可導的(導函數是連續函數),因此適合用在BP神經網絡中。(BP算法要求激活函數可導)
?
3. 神經網絡模型?
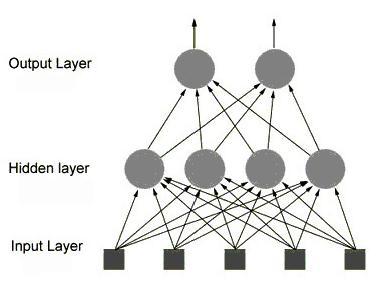
?????? 神經網絡是由大量的神經元互聯而構成的網絡。根據網絡中神經元的互聯方式,常見網絡結構主要可以分為下面3類:
(1) 前饋神經網絡 ( Feedforward Neural Networks )
?????? 前饋網絡也稱前向網絡。這種網絡只在訓練過程會有反饋信號,而在分類過程中數據只能向前傳送,直到到達輸出層,層間沒有向后的反饋信號,因此被稱為前饋網絡。感知機( perceptron)與BP神經網絡就屬于前饋網絡。
?????? 圖4 中是一個3層的前饋神經網絡,其中第一層是輸入單元,第二層稱為隱含層,第三層稱為輸出層(輸入單元不是神經元,因此圖中有2層神經元)。

圖4. 前饋神經網絡
?
對于一個3層的前饋神經網絡N,若用X表示網絡的輸入向量,W1~W3表示網絡各層的連接權向量,F1~F3表示神經網絡3層的激活函數。
那么神經網絡的第一層神經元的輸出為:
O1 = F1( XW1 )
第二層的輸出為:
O2 = F2 ( F1( XW1 ) W2 )
輸出層的輸出為:
O3 = F3( F2 ( F1( XW1 ) W2 ) W3 )
?????? 若激活函數F1~F3都選用線性函數,那么神經網絡的輸出O3將是輸入X的線性函數。因此,若要做高次函數的逼近就應該選用適當的非線性函數作為激活函數。
(2) 反饋神經網絡 ( Feedback Neural Networks )
?????? 反饋型神經網絡是一種從輸出到輸入具有反饋連接的神經網絡,其結構比前饋網絡要復雜得多。典型的反饋型神經網絡有:Elman網絡和Hopfield網絡。

圖5. 反饋神經網絡
?
(3) 自組織網絡 ( SOM ,Self-Organizing Neural Networks )
?????? 自組織神經網絡是一種無導師學習網絡。它通過自動尋找樣本中的內在規律和本質屬性,自組織、自適應地改變網絡參數與結構。

圖6. 自組織網絡
?
4. 神經網絡工作方式?
?????? 神經網絡運作過程分為學習和工作兩種狀態。
(1)神經網絡的學習狀態?
?????? 網絡的學習主要是指使用學習算法來調整神經元間的聯接權,使得網絡輸出更符合實際。學習算法分為有導師學習( Supervised Learning )與無導師學習( Unsupervised Learning )兩類。
?????? 有導師學習算法將一組訓練集 ( training set )送入網絡,根據網絡的實際輸出與期望輸出間的差別來調整連接權。有導師學習算法的主要步驟包括:
1)? 從樣本集合中取一個樣本(Ai,Bi);
2)? 計算網絡的實際輸出O;
3)? 求D=Bi-O;
4)? 根據D調整權矩陣W;
5) 對每個樣本重復上述過程,直到對整個樣本集來說,誤差不超過規定范圍。
BP算法就是一種出色的有導師學習算法。
?????? 無導師學習抽取樣本集合中蘊含的統計特性,并以神經元之間的聯接權的形式存于網絡中。
?????? Hebb學習律是一種經典的無導師學習算法。
(2) 神經網絡的工作狀態?
?????? 神經元間的連接權不變,神經網絡作為分類器、預測器等使用。
下面簡要介紹一下Hebb學習率與Delta學習規則 。
(3) 無導師學習算法:Hebb學習率?
Hebb算法核心思想是,當兩個神經元同時處于激發狀態時兩者間的連接權會被加強,否則被減弱。?
?????? 為了理解Hebb算法,有必要簡單介紹一下條件反射實驗。巴甫洛夫的條件反射實驗:每次給狗喂食前都先響鈴,時間一長,狗就會將鈴聲和食物聯系起來。以后如果響鈴但是不給食物,狗也會流口水。

圖7. 巴甫洛夫的條件反射實驗
?
受該實驗的啟發,Hebb的理論認為在同一時間被激發的神經元間的聯系會被強化。比如,鈴聲響時一個神經元被激發,在同一時間食物的出現會激發附近的另 一個神經元,那么這兩個神經元間的聯系就會強化,從而記住這兩個事物之間存在著聯系。相反,如果兩個神經元總是不能同步激發,那么它們間的聯系將會越來越 弱。
Hebb學習律可表示為:

?????? 其中wij表示神經元j到神經元i的連接權,yi與yj為兩個神經元的輸出,a是表示學習速度的常數。若yi與yj同時被激活,即yi與yj同時為正,那么Wij將增大。若yi被激活,而yj處于抑制狀態,即yi為正yj為負,那么Wij將變小。
(4) 有導師學習算法:Delta學習規則
Delta學習規則是一種簡單的有導師學習算法,該算法根據神經元的實際輸出與期望輸出差別來調整連接權,其數學表示如下:

?
?????? 其中Wij表示神經元j到神經元i的連接權,di是神經元i的期望輸出,yi是神經元i的實際輸出,xj表示神經元j狀態,若神經元j處于激活態則xj為 1,若處于抑制狀態則xj為0或-1(根據激活函數而定)。a是表示學習速度的常數。假設xi為1,若di比yi大,那么Wij將增大,若di比yi小, 那么Wij將變小。
?????? Delta規則簡單講來就是:若神經元實際輸出比期望輸出大,則減小所有輸入為正的連接的權重,增大所有輸入為負的連接的權重。反之,若神經元實際輸出比 期望輸出小,則增大所有輸入為正的連接的權重,減小所有輸入為負的連接的權重。這個增大或減小的幅度就根據上面的式子來計算。
(5)有導師學習算法:BP算法?
采用BP學習算法的前饋型神經網絡通常被稱為BP網絡。

圖8. 三層BP神經網絡結構
?
BP網絡具有很強的非線性映射能力,一個3層BP神經網絡能夠實現對任意非線性函數進行逼近(根據Kolrnogorov定理)。一個典型的3層BP神經網絡模型如圖7所示。
BP網絡的學習算法占篇幅較大,我打算在下一篇文章中介紹。
?
第二節、神經網絡實現?
?
1. 數據預處理?
?????? 在訓練神經網絡前一般需要對數據進行預處理,一種重要的預處理手段是歸一化處理。下面簡要介紹歸一化處理的原理與方法。
(1) 什么是歸一化??
數據歸一化,就是將數據映射到[0,1]或[-1,1]區間或更小的區間,比如(0.1,0.9) 。
(2) 為什么要歸一化處理??
<1>輸入數據的單位不一樣,有些數據的范圍可能特別大,導致的結果是神經網絡收斂慢、訓練時間長。
<2>數據范圍大的輸入在模式分類中的作用可能會偏大,而數據范圍小的輸入作用就可能會偏小。
<3> 由于神經網絡輸出層的激活函數的值域是有限制的,因此需要將網絡訓練的目標數據映射到激活函數的值域。例如神經網絡的輸出層若采用S形激活函數,由于S形 函數的值域限制在(0,1),也就是說神經網絡的輸出只能限制在(0,1),所以訓練數據的輸出就要歸一化到[0,1]區間。
<4>S形激活函數在(0,1)區間以外區域很平緩,區分度太小。例如S形函數f(X)在參數a=1時,f(100)與f(5)只相差0.0067。
(3) 歸一化算法?
一種簡單而快速的歸一化算法是線性轉換算法。線性轉換算法常見有兩種形式:
?????? <1>
y = ( x - min )/( max - min )
其中min為x的最小值,max為x的最大值,輸入向量為x,歸一化后的輸出向量為y 。上式將數據歸一化到 [ 0 , 1 ]區間,當激活函數采用S形函數時(值域為(0,1))時這條式子適用。
?????? <2>
y = 2 * ( x - min ) / ( max - min ) - 1
?????? 這條公式將數據歸一化到 [ -1 , 1 ] 區間。當激活函數采用雙極S形函數(值域為(-1,1))時這條式子適用。
(4) Matlab數據歸一化處理函數?
Matlab中歸一化處理數據可以采用premnmx , postmnmx , tramnmx 這3個函數。
<1> premnmx
語法:[pn,minp,maxp,tn,mint,maxt] = premnmx(p,t)
參數:
pn: p矩陣按行歸一化后的矩陣
minp,maxp:p矩陣每一行的最小值,最大值
tn:t矩陣按行歸一化后的矩陣
mint,maxt:t矩陣每一行的最小值,最大值
作用:將矩陣p,t歸一化到[-1,1] ,主要用于歸一化處理訓練數據集。
<2> tramnmx
語法:[pn] = tramnmx(p,minp,maxp)
參數:
minp,maxp:premnmx函數計算的矩陣的最小,最大值
pn:歸一化后的矩陣
作用:主要用于歸一化處理待分類的輸入數據。
<3> postmnmx
語法: [p,t] =postmnmx(pn,minp,maxp,tn,mint,maxt)
參數:
minp,maxp:premnmx函數計算的p矩陣每行的最小值,最大值
mint,maxt:premnmx函數計算的t矩陣每行的最小值,最大值
作用:將矩陣pn,tn映射回歸一化處理前的范圍。postmnmx函數主要用于將神經網絡的輸出結果映射回歸一化前的數據范圍。
2. 使用Matlab實現神經網絡?
使用Matlab建立前饋神經網絡主要會使用到下面3個函數:
newff :前饋網絡創建函數
train:訓練一個神經網絡
sim :使用網絡進行仿真
?下面簡要介紹這3個函數的用法。
(1) newff函數
<1>newff函數語法?
?????? newff函數參數列表有很多的可選參數,具體可以參考Matlab的幫助文檔,這里介紹newff函數的一種簡單的形式。
語法:net = newff ( A, B, {C} ,‘trainFun’)
參數:
A:一個n×2的矩陣,第i行元素為輸入信號xi的最小值和最大值;
B:一個k維行向量,其元素為網絡中各層節點數;
C:一個k維字符串行向量,每一分量為對應層神經元的激活函數;
trainFun :為學習規則采用的訓練算法。
<2>常用的激活函數
常用的激活函數有:
a) 線性函數 (Linear transfer function)
f(x) = x
該函數的字符串為’purelin’。
?
b) 對數S形轉移函數( Logarithmic sigmoid transfer function )

??? 該函數的字符串為’logsig’。
c) 雙曲正切S形函數 (Hyperbolic tangent sigmoid transfer function )

也就是上面所提到的雙極S形函數。
?
該函數的字符串為’ tansig’。
Matlab的安裝目錄下的toolbox\nnet\nnet\nntransfer子目錄中有所有激活函數的定義說明。
<3>常見的訓練函數
??? 常見的訓練函數有:
traingd :梯度下降BP訓練函數(Gradient descentbackpropagation)
traingdx :梯度下降自適應學習率訓練函數
<4>網絡配置參數
一些重要的網絡配置參數如下:
net.trainparam.goal ?:神經網絡訓練的目標誤差
net.trainparam.show ??: 顯示中間結果的周期
net.trainparam.epochs :最大迭代次數
net.trainParam.lr ?? : 學習率
(2) train函數
??? 網絡訓練學習函數。
語法:[ net, tr, Y1, E ]? = train( net, X, Y )
參數:
X:網絡實際輸入
Y:網絡應有輸出
tr:訓練跟蹤信息
Y1:網絡實際輸出
E:誤差矩陣
(3) sim函數
語法:Y=sim(net,X)
參數:
net:網絡
X:輸入給網絡的K×N矩陣,其中K為網絡輸入個數,N為數據樣本數
Y:輸出矩陣Q×N,其中Q為網絡輸出個數
(4) Matlab BP網絡實例?
?????? 我將Iris數據集分為2組,每組各75個樣本,每組中每種花各有25個樣本。其中一組作為以上程序的訓練樣本,另外一組作為檢驗樣本。為了方便訓練,將3類花分別編號為1,2,3 。
使用這些數據訓練一個4輸入(分別對應4個特征),3輸出(分別對應該樣本屬于某一品種的可能性大小)的前向網絡。
?????? Matlab程序如下:
?
以上程序的識別率穩定在95%左右,訓練100次左右達到收斂,訓練曲線如下圖所示:

圖9. 訓練性能表現
?
(5)參數設置對神經網絡性能的影響?
?????? 我在實驗中通過調整隱含層節點數,選擇不通過的激活函數,設定不同的學習率,
?
<1>隱含層節點個數?
隱含層節點的個數對于識別率的影響并不大,但是節點個數過多會增加運算量,使得訓練較慢。
?
<2>激活函數的選擇?
?????? 激活函數無論對于識別率或收斂速度都有顯著的影響。在逼近高次曲線時,S形函數精度比線性函數要高得多,但計算量也要大得多。
?
<3>學習率的選擇?
?????? 學習率影響著網絡收斂的速度,以及網絡能否收斂。學習率設置偏小可以保證網絡收斂,但是收斂較慢。相反,學習率設置偏大則有可能使網絡訓練不收斂,影響識別效果。
?
3. 使用AForge.NET實現神經網絡?
(1) AForge.NET簡介?
?????? AForge.NET是一個C#實現的面向人工智能、計算機視覺等領域的開源架構。AForge.NET源代碼下的Neuro目錄包含一個神經網絡的類庫。
AForge.NET主頁:http://www.aforgenet.com/
AForge.NET代碼下載:http://code.google.com/p/aforge/
Aforge.Neuro工程的類圖如下:
?

圖10. AForge.Neuro類庫類圖
?
下面介紹圖9中的幾個基本的類:
Neuron —神經元的抽象基類
Layer — 層的抽象基類,由多個神經元組成
Network —神經網絡的抽象基類,由多個層(Layer)組成
IActivationFunction - 激活函數(activation function)的接口
IUnsupervisedLearning - 無導師學習(unsupervised learning)算法的接口ISupervisedLearning - 有導師學習(supervised learning)算法的接口
?
(2)使用Aforge建立BP神經網絡?
?????? 使用AForge建立BP神經網絡會用到下面的幾個類:
<1> ?SigmoidFunction : S形神經網絡
構造函數:public SigmoidFunction( doublealpha )
參數alpha決定S形函數的陡峭程度。
<2>? ActivationNetwork :神經網絡類
構造函數:
public ActivationNetwork( IActivationFunction function, int inputsCount, paramsint[] neuronsCount )
???????????????????????? : base(inputsCount, neuronsCount.Length )
public virtual double[] Compute( double[]input )
?
參數意義:
inputsCount:輸入個數
neuronsCount :表示各層神經元個數
<3>? BackPropagationLearning:BP學習算法
?構造函數:
public BackPropagationLearning( ActivationNetwork network )
?參數意義:
network :要訓練的神經網絡對象
BackPropagationLearning類需要用戶設置的屬性有下面2個:
learningRate :學習率
momentum :沖量因子
下面給出一個用AForge構建BP網絡的代碼。
?
?
?????? 改程序對Iris 數據進行分類,識別率可達97%左右 。
?
?? ? 點擊下載源代碼
?
文章來自:http://www.cnblogs.com/heaad/ ?
?








)
 RE的歡迎來看看)




4.pdf)


~~~~)


