POJ 1228 Grandpa's Estate --深入理解凸包

題意： 判斷凸包是否穩定。

解法： 穩定凸包每條邊上至少有三個點。

這題就在于求凸包的細節了，求凸包有兩種算法：?

1.基于水平序的Andrew算法

2.基于極角序的Graham算法

兩種算法都有一個類似下面的語句：

for(int i=0;i<n;i++) {while(m > 1 && Cross(ch[m-1]-ch[m-2], p[i]-ch[m-2]) <= 0) m--;ch[m++] = p[i];}

這樣的話，求出來就是最簡凸包，即點數盡量少的凸包，因為Cross == 0的情況也被出棧了，所以一條凸包邊上就會三點共線了。

我們把語句改下，把Cross.. <=0 ?改成 Cross.. < 0 ，那么求的就是最繁凸包，即可能一條凸包邊上包含很多點也屬于凸包的點。

即下面的情況：

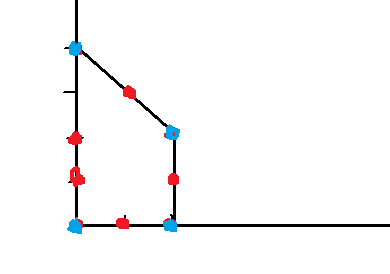
最簡凸包即為藍色的四個點。 最繁凸包求出的是所有藍點和紅點。

作為這個題，我們怎么求其實都可以：

1.如果求最簡凸包，我們只需判斷總共有多少個點在該凸包邊上即可（端點也算），如果 < 3 ，則不符。

2.如果求的是最繁的凸包，就不能用上面的判法，因為怎么判都只有兩個點了，這時候可以采用下面的方法：

假設要判斷的邊i，那么判斷邊i和邊i-1，邊i和邊i+1的夾角是否都為0（180）。                                        ----XDruid

?

代碼： （這里我用的是Andrew算法）

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <cmath>
#include <algorithm>
#define eps 1e-8
using namespace std;struct Point{double x,y;Point(double x=0, double y=0):x(x),y(y) {}void input() { scanf("%lf%lf",&x,&y); }
};
typedef Point Vector;
int dcmp(double x) {if(x < -eps) return -1;if(x > eps) return 1;return 0;
}
template <class T> T sqr(T x) { return x * x;}
Vector operator + (Vector A, Vector B) { return Vector(A.x + B.x, A.y + B.y); }
Vector operator - (Vector A, Vector B) { return Vector(A.x - B.x, A.y - B.y); }
Vector operator * (Vector A, double p) { return Vector(A.x*p, A.y*p); }
Vector operator / (Vector A, double p) { return Vector(A.x/p, A.y/p); }
bool operator < (const Point& a, const Point& b) { return a.x < b.x || (a.x == b.x && a.y < b.y); }
bool operator >= (const Point& a, const Point& b) { return a.x >= b.x && a.y >= b.y; }
bool operator <= (const Point& a, const Point& b) { return a.x <= b.x && a.y <= b.y; }
bool operator == (const Point& a, const Point& b) { return dcmp(a.x-b.x) == 0 && dcmp(a.y-b.y) == 0; }
double Dot(Vector A, Vector B) { return A.x*B.x + A.y*B.y; }
double Length(Vector A) { return sqrt(Dot(A, A)); }
double Angle(Vector A, Vector B) { return acos(Dot(A, B) / Length(A) / Length(B)); }
double Cross(Vector A, Vector B) { return A.x*B.y - A.y*B.x; }
double angle(Vector v) { return atan2(v.y, v.x); }bool OnSegment(Point P, Point A, Point B) {         //端點不算return dcmp(Cross(A-P,B-P)) == 0 && dcmp(Dot(A-P,B-P)) <= 0;
}
int ConvexHull(Point* p, int n, Point* ch) {sort(p,p+n);int m = 0;for(int i=0;i<n;i++) {while(m > 1 && Cross(ch[m-1]-ch[m-2], p[i]-ch[m-2]) <= 0) m--;ch[m++] = p[i];}int k = m;for(int i=n-2;i>=0;i--) {while(m > k && Cross(ch[m-1]-ch[m-2], p[i]-ch[m-2]) <= 0) m--;ch[m++] = p[i];}if(n > 1) m--;return m;
}
Point ch[1006],p[1006];int main()
{int t,n,i,j;scanf("%d",&t);while(t--){scanf("%d",&n);for(i=0;i<n;i++) p[i].input();if(n <= 5) { puts("NO"); continue; }int m = ConvexHull(p,n,ch);if(m <= 2) { puts("NO"); continue; }for(i=0;i<m;i++) {int cnt = 0;for(j=0;j<n;j++)if(OnSegment(p[j],ch[i],ch[(i+1)%m]))cnt++;if(cnt < 3) break;}if(i == m) puts("YES");else       puts("NO");}return 0;
}

?

現在終于對自己的凸包版有了全面的了解了，媽媽再也不用擔心我用錯凸包了。哈哈。