分治法

我們首先先介紹分治法。分治法的思想：將原問題分解為幾個規模較小但類似于原問題的子問題，遞歸地求解這些子問題，然后在合并這些子問題的解來解決原問題的解。

還是拿撲克牌舉例子，假設桌上有兩堆牌面朝上的牌(牌面朝上：有值)，每堆都已排序，最小的牌在頂上。我們希望把這兩堆牌合并成單一的排好序的輸出堆，牌面朝下地放在桌上。應該怎么做呢？

我們的做法是：在牌面朝上的兩堆牌的頂上兩張牌中選取較小的一張，將該牌從其堆中移開(該堆的頂上將顯示一張新牌)并牌面朝下地將該牌放置到輸出堆。重復這個步驟直到兩堆牌都沒有牌。

下面我們來實現上面所提的思想

為了避免在某個基本步驟必須檢查是否有堆為空。在每個堆的底部放置一張哨兵牌，它包含一個特殊的值(很大的值，使它不可能是較小的牌，除非兩個堆都已顯露出其哨兵牌。一旦發生這種情況，說明非哨兵牌都已被放置到輸出堆)，用于簡化代碼。

偽代碼：

MERGE(A,p,q,r)

n1 = q - p + 1

n2 = r - q

//L[1..n1+1] and R[1..n2+1]是新的數組

for i = 1 to n1

L[i] = A[p + i -1]

for j = 1 to n2

R[j] = A[q + j]

L[n1 + 1] = ∞

R[n2 + 1] = ∞

i = 1

j = 1

for k = p to r

if L[i] <= R[j]

A[k] = L[i]

i = i + 1

else

A[k] = R[j]

j = j + 1

Java實現：

public void Merge(int[] A,int p,int q,int r){

int n1 = q - p + 1;

int n2 = r - q;

//L[1..n1+1] and R[1..n2+1]是新的數組

int[] L = new int[n1 + 1];

int[] R = new int[n2 + 1];

for (int i = 0;i < n1;i++){

L[i] = A[p + i];

}

for (int j = 0;j < n2;j++){

R[j] = A[q + j + 1];

}

L[n1] = Integer.MAX_VALUE;

R[n2] = Integer.MAX_VALUE;

int i = 0,j = 0;

for (int k = p;k <= r;k++){

if (L[i] <= R[j]){

A[k] = L[i];

i = i + 1;

}else{

A[k] = R[j];

j = j + 1;

}

}

}

下面我們來看一下分治法的步驟

對數組A[2,4,7,1,3,6]調用Merge(A,0,2,5)

初始狀態

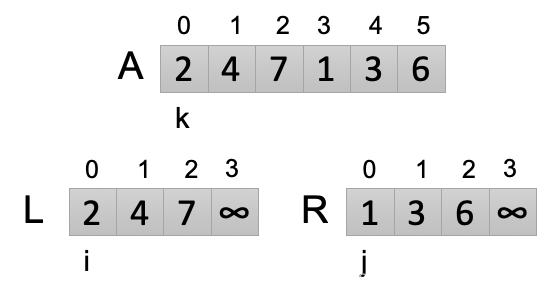
初始完L和R數組之后，現在進入for循環階段。讓L中i所指的值和R數組中j所指的值進行比較，把較小的值放入數組A中k所指的位置。并且讓較小的值的索引i或j前進一格(+1)。因為L和R數組已經從小到大排好序了，所以找出來的最小值一定是當前L和R數組的最小值，放入了數組A中也是排好序的，所以讓k前進一步，k=k+1,然后執行下一次循環。

第一此循環：i和j初始為0，k=p=0，讓L[0]與R[0]進行比較 L[0]>R[0]所以R[0]是較小值，把A[0]替換為R[0]。讓j=j+1，i保持不變。k=k+1=1，開啟下一次循環。本次循環結果如下圖所示：

A中的灰色位置包含將被覆蓋的值，L和R中的灰色位置包含有待于被復制回A的值，A中的黃色位置包含它們的最終值，L和R中的黃色位置包含已被復制回A的值。

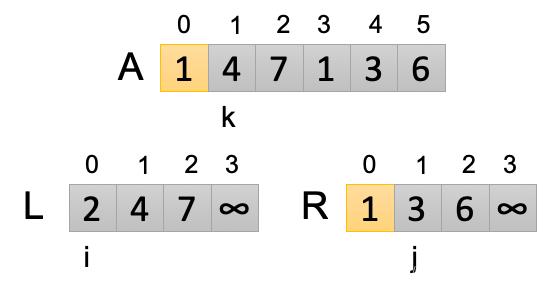
第二次循環：此時i=0，j=1，k=1，讓L[i]和R[j]進行比較，L[0]

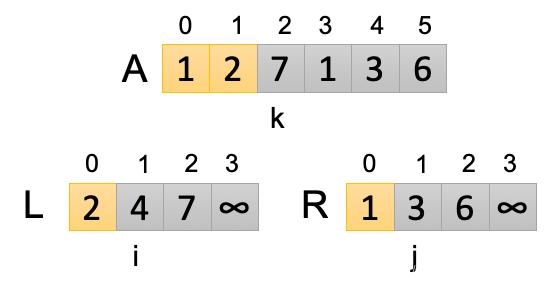
第三次循環：此時i=1，j=1，k=2，讓L[i]和R[j]進行比較，L[1]>R[1]，所以R[1]是較小值，把A[2]即A[2]替換為R[1]。讓j=j+1，i保存不變。k=k+1=3，開啟下一次循環。本次循環結果如下圖所示：

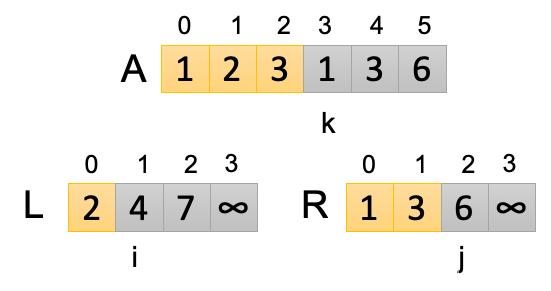
第四次循環：此時i=1，j=2，k=3，讓L[i]和R[j]進行比較，L[1]

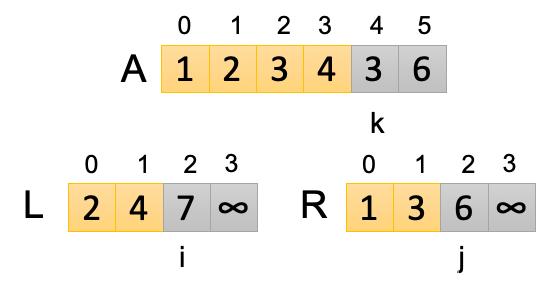
第五次循環：此時i=2，j=2，k=4，讓L[i]和R[j]進行比較，L[2]>R[2]，所以R[2]是較小值，把A[k]即A[4]替換為R[2]。讓j=j+1，j保存不變。k=k+1=4，開啟下一次循環。本次循環結果如下圖所示：

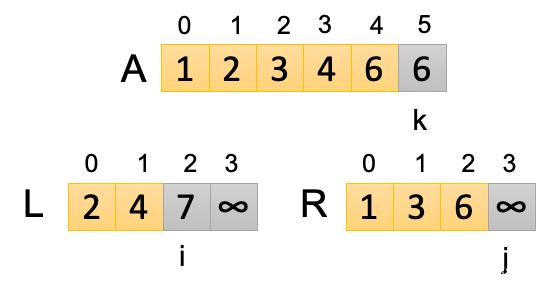
注意：此時j已經到達了R數組的最后一個數∞，L數組中的每個數都比∞小，即不等式L[i]>R[j]恒成立。所以不管L剩下多少個數，都會按照順序放置A中，直到i也達到了最后一個數∞，此時k>r，循環已經全部結束。

第六次循環：此時i=2，j=3，k=5，讓L[i]和R[j]進行比較，L[2]

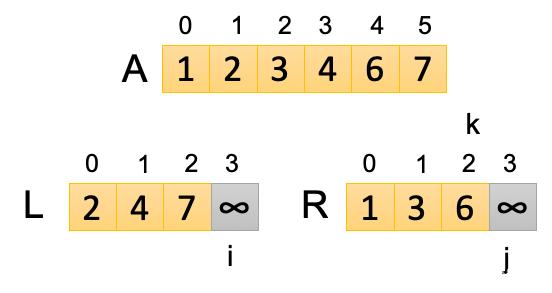
第七次循環，此時i=2，j=3，k=6，我們的r=5，判斷條件k<=r為false，循環結束。

分治法的應用——歸并排序

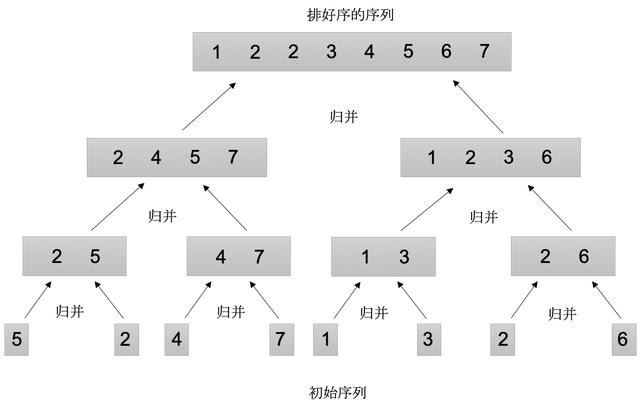
上面講到了分治法，分治法有個很大的限制就是L和R是排好序的才可以。但是許多數組都是很亂的順序。那么怎么解決這個問題呢？試想一下如果L和R數組的大小為1，那么L和R數組肯定是排好序的。對的！我們可以把一個大的數組遞歸拆分成小的子數組，子數組在遞歸拆分成更小的子數組。直到遞歸到的L和R數組的大小為1時，調用MERGE分治法。隨著算法自底向上地推進：合并只含1項的序列對形成長度為2的排好序的序列，合并長度為2的序列對形成長度為4的排好序的序列，依次下去，直到長度為n/2的兩個序列被合并最終形成長度為n的排好序的序列，數組最終會排序完成。

如下圖所示

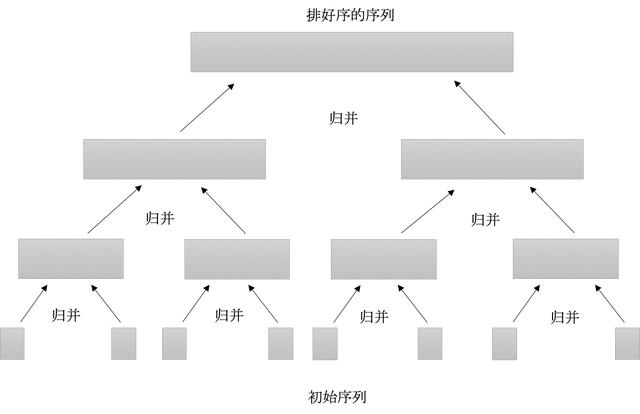
我們可以把上面提到的MERGE作為歸并排序算法中的一個子程序來用。

下面的過程MERGE-SORT(A,p,r)排序子數組A[p…r]中的元素。若p>=r,則該子數組最多有一個元素，所以已經排好序。否則，分解步驟簡單地計算一個下標q，將A[p…r]分成兩個子數組A[p…q]和A[q+1…r]，前者包含?n/2?個元素，后者包含?n/2?個元素。

偽代碼：

MERGE-SORT(A,p,r)

if p < r

q = ?(p+r)/2?

MERGE-SORT(A,p,q)

MERGE-SORT(A,q+1,r)

MERGE(A,p,q,r)

java實現：

public void MergeSort(int[] A,int p,int r) {

if (p < r){

int q =(int)Math.floor((p+r)/2);

MergeSort(A,p,q); //將左半邊排序

MergeSort(A,q+1,r); //將右半邊排序

Merge(A,p,q,r); //歸并結果

}

}

下面我們來看一下歸并排序在數組A=[5,2,4,7,1,3,2,6]上的操作，隨著算法自底向上地推進，待合并的已排好序的各序列的長度不斷增加。