第二章? 線性規劃（重點：單純形法）

1.線性規劃問題及其模型（重點：標準形式）

題型：是否為標準形式？不是的話化為標準形式！

1）問題的提出

提出問題：利率最大化???

確定決策變量>>>定義目標函數>>>確定約束條件>>>數學模型

2）基本概念

3）線性規劃問題的共同特征：線性——最高次數為1

4）線性規劃問題的一般形式與標準形式

①一般形式：><——表示可以大于也可以小于

②標準形式：三大特征——目標函數最小化、約束條件等式、決策變量非負

5）線性規劃問題的標準化（按照標準形式三特征進行修改）

?

例1：非負松弛變量："<="變為"="——加上一個非負松弛變量使得等式可以成立

一般式：

標準化后：

?

例2：剩余變量：“>=”變為“=”——減去一個非負剩余變量（見例3）

?

例3：可正可負（無約束）變為“=”——用兩個非負變量來代替那個無約束變量

2.線性規劃求解基本原理

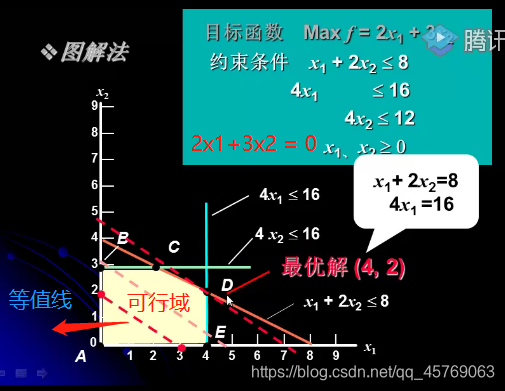
2.1 圖解法（根據約束條件在坐標系中畫出可行域，尋求最優解）

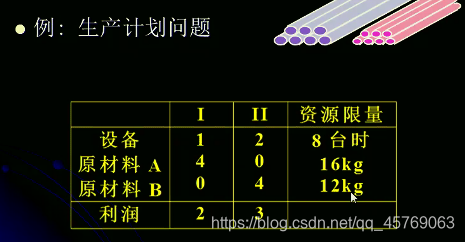
例1：

步驟：

1）可行域繪制

2）畫目標函數的等值線（得到目標函數的斜率，一般令f=0）

3)移動等值線，往最優方向移動，直到不能移動

注：線性規劃問題求解的幾種可能結果

1）唯一解：只有一個解

2）無窮解：等值線與邊界平行

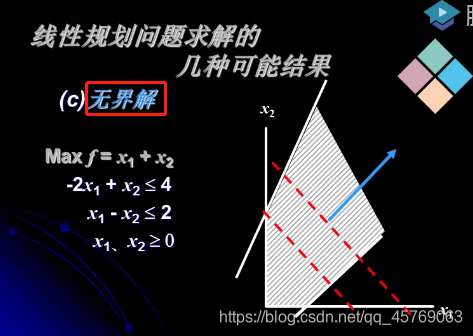
3）無界解：可行域在最優的方向沒有邊界

4）無可行解：可行域為空集

?

2.2? 線性規劃問題解的概念

1. 可行解+最優解

正在上傳…重新上傳取消?

2.基：若B矩陣是A矩陣的非負子矩陣（|B|不等于0），則稱B為A的一個基矩陣

?

?