????Erode腐蝕， Dilate膨脹，這兩個形態學函數總是成對出現，前者可以消除較小的點如噪音，后者可以使不連通的圖像合并成塊。

void cvErode( const CvArr* src, CvArr* dst, IplConvKernel* element=NULL, int iterations=1 );
void cvDilate( const CvArr* src, CvArr* dst, IplConvKernel* element=NULL, int iterations=1 );

#include<iostream>  
#include <opencv2/core/core.hpp>  
#include <opencv2/highgui/highgui.hpp>  #include "cv.h"
#include "cxcore.h"
#include "highgui.h"
int main(int argc, char** argv)
{if (argc<2)return 0;//檢查輸入參數int a = 1;int eIter = 1, dIter = 1, exitFlag = 1;IplImage *image, *image1, *image2;image = cvLoadImage(argv[1]);image1 = cvCreateImage(cvSize(image->width, image->height), 8, 1);//創建首地址并分配存儲空間image2 = cvCreateImage(cvSize(image->width, image->height), 8, 1);cvCvtColor(image, image1, CV_RGB2GRAY);//實現RGB顏色向HSV,HSI等顏色空間的轉換. 參數CV_RGB2GRAY是RGB到gray(灰度圖）c參數 CV_GRAY2RGB是gray到RGB.cvCvtColor(image, image2, CV_RGB2GRAY);cvNamedWindow("image", 1);cvShowImage("image", image);/* 對話框未使用cvNamedWindow("Select", 1);cvCreateTrackbar("eIterations", "Select", &eIter, 20, 0); //參數1滑塊名稱  參數2顯示窗口  參數3 OPENCV將當前滑塊位置值傳給指針指向的整數   參數4滑塊調整范圍最大值  參數5指向回調函數的指針，當滑動條被拖動時，函數自動調用  cvCreateTrackbar("dIterations", "Select", &dIter, 20, 0);//參數1滑塊名稱  參數2顯示窗口  參數3 OPENCV將當前滑塊位置值傳給指針指向的整數   參數4滑塊調整范圍最大值  參數5指向回調函數的指針，當滑動條被拖動時，函數自動調用*/cvNamedWindow("Erode_fushi", 1);cvNamedWindow("Dilate_pengzhang", 1);cvShowImage("Erode_fushi", image1);cvShowImage("Dilate_pengzhang", image2);cvWaitKey(0);while (1){cvErode(image1, image1, 0, 1);		/*cvErode腐蝕，消除細小物質src  輸入圖像.dst  輸出圖像.element   用于腐蝕的結構元素。若為 NULL, 則使用 3×3 長方形的結構元素iterations   腐蝕的次數.  腐蝕可以重復進行(iterations) 次.對彩色圖像，每個彩色通道單獨處理。*/cvShowImage("Erode_fushi", image1);std::cout << "Erode_fushi" << std::endl;a = cvWaitKey(0);if ((char)a == 'q')break;}cvCopy(image1, image2);a = 1;while (1){cvDilate(image2, image2, 0, 1);		//膨脹，填充物體內細小物質/*cvDilate膨脹，消除細小物質src  輸入圖像.dst  輸出圖像.element   用于膨脹的結構元素。若為 NULL, 則使用 3×3 長方形的結構元素iterations   膨脹的次數.  膨脹可以重復進行(iterations) 次.對彩色圖像，每個彩色通道單獨處理。*/cvShowImage("Dilate_pengzhang", image2);std::cout << "Dilate_pengzhang" << std::endl;a = cvWaitKey(0);if ((char)a == 'q')break;}//釋放窗口資源return 0;
}

原圖：

腐蝕：

膨脹：

一???引言
???????數學形態學是一門建立在集論基礎上的學科，是幾何形態學分析和描述的有力工具。數學形態學的歷史可回溯到19世紀。1964年法國的Matheron和Serra在積分幾何的研究成果上，將數學形態學引入圖像處理領域，并研制了基于數學形態學的圖像處理系統。1982年出版的專著《ImageAnalysis and MathematicalMorphology》是數學形態學發展的重要里程碑，表明數學形態學在理論上趨于完備及應用上不斷深入。數學形態學蓬勃發展，由于其并行快速，易于硬件實現，已引起了人們的廣泛關注。目前，數學形態學已在計算機視覺、信號處理與圖像分析、模式識別、計算方法與數據處理等方面得到了極為廣泛的應用。
???????數學形態學可以用來解決抑制噪聲、特征提取、邊緣檢測、圖像分割、形狀識別、紋理分析、圖像恢復與重建、圖像壓縮等圖像處理問題。該文將主要對數學形態學的基本理論及其在圖像處理中的應用進行綜述。

二???數學形態學的定義和分類
???????數學形態學是以形態結構元素為基礎對圖像進行分析的數學工具。它的基本思想是用具有一定形態的結構元素去度量和提取圖像中的對應形狀以達到對圖像分析和識別的目的。數學形態學的應用可以簡化圖像數據，保持它們基本的形狀特征，并除去不相干的結構。數學形態學的基本運算有4個：膨脹、腐蝕、開啟和閉合。它們在二值圖像中和灰度圖像中各有特點。基于這些基本運算還可以推導和組合成各種數學形態學實用算法。

（1）二值形態學
???????數學形態學中二值圖像的形態變換是一種針對集合的處理過程。其形態算子的實質是表達物體或形狀的集合與結構元素間的相互作用，結構元素的形狀就決定了這種運算所提取的信號的形狀信息。形態學圖像處理是在圖像中移動一個結構元素，然后將結構元素與下面的二值圖像進行交、并等集合運算。
???????基本的形態運算是腐蝕和膨脹。
???????在形態學中，結構元素是最重要最基本的概念。結構元素在形態變換中的作用相當于信號處理中的“濾波窗口”。用B（x）代表結構元素，對工作空間E中的每一點x，腐蝕和膨脹的定義為：
???????
???????用B（x）對E進行腐蝕的結果就是把結構元素B平移后使B包含于E的所有點構成的集合。用B（x）對E進行膨脹的結果就是把結構元素B平移后使B與E的交集非空的點構成的集合。先腐蝕后膨脹的過程稱為開運算。它具有消除細小物體，在纖細處分離物體和平滑較大物體邊界的作用。先膨脹后腐蝕的過程稱為閉運算。它具有填充物體內細小空洞，連接鄰近物體和平滑邊界的作用。
???????可見，二值形態膨脹與腐蝕可轉化為集合的邏輯運算，算法簡單，適于并行處理，且易于硬件實現，適于對二值圖像進行圖像分割、細化、抽取骨架、邊緣提取、形狀分析。但是，在不同的應用場合，結構元素的選擇及其相應的處理算法是不一樣的，對不同的目標圖像需設計不同的結構元素和不同的處理算法。結構元素的大小、形狀選擇合適與否，將直接影響圖像的形態運算結果。因此，很多學者結合自己的應用實際，提出了一系列的改進算法。如梁勇提出的用多方位形態學結構元素進行邊緣檢測算法既具有較好的邊緣定位能力，又具有很好的噪聲平滑能力。許超提出的以最短線段結構元素構造準圓結構元素或序列結構元素生成準圓結構元素相結合的設計方法，用于骨架的提取，可大大減少形態運算的計算量，并可同時滿足尺度、平移及旋轉相容性，適于對形狀進行分析和描述。

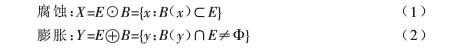
（2）灰度數學形態學
???????二值數學形態學可方便地推廣到灰度圖像空間。只是灰度數學形態學的運算對象不是集合，而是圖像函數。以下設f（x，y）是輸入圖像，b（x，y）是結構元素。用結構元素b對輸入圖像y進行膨脹和腐蝕運算分別定義為：

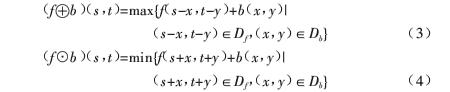
對灰度圖像的膨脹（或腐蝕）操作有兩類效果：
（1）如果結構元素的值都為正的，則輸出圖像會比輸入圖像亮（或暗）；
（2）根據輸入圖像中暗（或亮）細節的灰度值以及它們的形狀相對于結構元素的關系，它們在運算中或被消減或被除掉。灰度數學形態學中開啟和閉合運算的定義與在二值數學形態學中的定義一致。用b對f進行開啟和閉合運算的定義為：

（3）模糊數學形態學
???????將模糊集合理論用于數學形態學就形成了模糊形態學。模糊算子的定義不同，相應的模糊形態運算的定義也不相同。在此，選用Shinba的定義方法。模糊性由結構元素對原圖像的適應程度來確定。用有界支撐的模糊結構元素對模糊圖像的腐蝕和膨脹運算按它們的隸屬函數定義為：

?

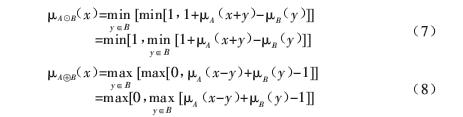
其中，x,y∈Z²代表空間坐標，u_a，u_b分別代表圖像和結構元素的隸屬函數。從（7），（8）式的結果可知，經模糊形態腐蝕膨脹運算后的隸屬函數均落在[0,1]的區間內。模糊形態學是傳統數學形態學從二值邏輯向模糊邏輯的推廣，與傳統數學形態學有相似的計算結果和相似的代數特性。模糊形態學重點研究n維空間目標物體的形狀特征和形態變換，主要應用于圖像處理領域，如模糊增強、模糊邊緣檢測、模糊分割等。

?

三?數學形態學在圖像處理中的主要應用

?

近年來，數學形態學在圖像處理方面得到了日益廣泛的應用。下面主要就數學形態學在邊緣檢測、圖像分割、圖像細化以及噪聲濾除等方面的應用做簡要介紹。

?

（1）???????邊緣檢測

邊緣檢測是大多數圖像處理必不可少的一步，提供了物體形狀的重要信息。對于二值圖像，邊緣檢測是求一個集合A的邊界，記為B（A）：

?

?

對于灰度圖像，邊緣檢測是求一幅圖像的形態學梯度，記為g：

?

?

數學形態學運算用于邊緣檢測，存在著結構元素單一的問題。它對與結構元素同方向的邊緣敏感，而與其不同方向的邊緣（或噪聲）會被平滑掉，即邊緣的方向可以由結構元素的形狀確定。但如果采用對稱的結構元素，又會減弱對圖像邊緣的方向敏感性。所以在邊緣檢測中，可以考慮用多方位的形態結構元素，運用不同的結構元素的邏輯組合檢測出不同方向的邊緣。

梁勇等人構造了8個方向的多方位形態學結構元素，應用基本形態運算，得到8個方向的邊緣檢測結果，再把這些結果進行歸一化運算、加權求和，得到最終的圖像邊緣。該算法在保持圖像細節特征和平滑邊緣等方面，取得了較好的效果。

?

（2）???????圖像分割

基于數學形態學的圖像分割算法是利用數學形態學變換，把復雜目標X分割成一系列互不相交的簡單子集X₁，X₂，…，X_N，即：

?

對目標X的分割過程可按下面的方法完成：首先求出X的最大內接“圓”X₁，然后將X₁從X中減去，再求X-X₁的最大內接“圓”X₂，…，依此類推，直到最后得到的集合為空集為止。下面以二值圖像為例，介紹用數學形態學方法求解子集X₁，X₂，…，X_N的過程。

設B為結構元素，B可以是圓、三角形、正方形等簡單的幾何基元，那么“簡單”形狀集合X_i可以用下面的公式來定義：

?

式中n_i為一整數，用上式定義X_i分割目標，有時會產生分割過程不唯一的現象。為此可采用下面公式來定義簡單集合X_i：

?

其中L_i為一個點或一條線，當L_i為點時，則與（12）式定義等價。（13）式定義的簡單形狀X_i可由n_iB沿線L_i移動而產生。即將“產生器”n_iB的中心沿“脊骨”L_i移動產生。如果n_iB為圓，則得到的X_i稱Blum帶。它具有一些特殊的性質，如X_i的邊界是光滑的，X_i的最大圓與其邊界相切，X_i的脊骨與產生器都是唯一的等等。

有了簡單形狀集合X_i的定義，則目標X可按下面方法分割。首先按式（14）求出X的最大內切結構元素X_i：

?

?

數學形態學用于圖像分割的缺點是對邊界噪聲敏感。為了改善這一問題，劉志敏等人提出了基于圖像最大內切圓的數學形態學形狀描述圖像分割算法和基于目標最小閉包結構元素的數學形態學形狀描述圖像分割算法，并使用該算法對二值圖像進行了分割，取得了較好的效果。鄧世偉等人提出一種基于數學形態學的深度圖像分割算法。作者首先利用形態學算子獲得分別含有階躍邊緣與屋脊邊緣的凸脊和凹谷圖像，然后利用控制區域生長過程得到最終的分割結果。與傳統方法相比，該方法速度快，抗噪性能好。

?

（3）???????形態骨架提取

形態骨架描述了物體的形狀和方向信息。它具有平移不變性、逆擴張性和等冪性等性質，是一種有效的形狀描述方法。二值圖像A的形態骨架可以通過選定合適的結構元素B，對A進行連續腐蝕和開啟運算來求取，設S（A）代表A的骨架，定義為：

?

蔣剛毅等人運用數學形態學方法，對交通標志的內核形狀提取形態骨架函數，將其作為用于模式匹配的形狀特征。A的形態骨架函數SKF（A）表示為：

?

SKF（X）中值較大的點對應大的n，并代表了形態骨架的主要成分，即表達了形狀的主體結構；而SKF（X）中值較小的點對應小的n，是形態骨架的細節成分，與形狀的邊緣信息相聯系。

形態骨架函數完整簡潔地表達了形態骨架的所有信息，因此，根據形態骨架函數的模式匹配能夠實現對不同形狀物體的識別。算法具有位移不變性，因而使識別更具穩健性。

?

（4）???????噪聲濾除

對圖像中的噪聲進行濾除是圖像預處理中不可缺少的操作。將開啟和閉合運算結合起來可構成形態學噪聲濾除器。

對于二值圖像，噪聲表現為目標周圍的噪聲塊和目標內部的噪聲孔。用結構元素B對集合A進行開啟操作，就可以將目標周圍的噪聲塊消除掉；用B對A進行閉合操作，則可以將目標內部的噪聲孔消除掉。該方法中，對結構元素的選取相當重要，它應當比所有的噪聲孔和噪聲塊都要大。

對于灰度圖像，濾除噪聲就是進行形態學平滑。實際中常用開啟運算消除與結構元素相比尺寸較小的亮細節，而保持圖像整體灰度值和大的亮區域基本不變；用閉合運算消除與結構元素相比尺寸較小的暗細節，而保持圖像整體灰度值和大的暗區域基本不變。將這兩種操作綜合起來可達到濾除亮區和暗區中各類噪聲的效果。同樣的，結構元素的選取也是個重要問題。

?

四?選取結構元素的方法

分析表明，各種數學形態學算法的應用可分解為形態學運算和結構元素選擇兩個基本問題，形態學運算的規則已由定義確定，于是形態學算法的性能就取決于結構元素的選擇，亦即結構元素決定著形態學算法的目的和性能。因此如何自適應地優化確定結構元素，就成為形態學領域中人們長期關注的研究熱點和技術難點。目前較多采用多個結構元素對圖像進行處理的方法。

?

（1）???????多結構元素運算

在許多形態學應用中，往往只采用一個結構元素，這通常不能產生滿意的結果。在模式識別中，如果要提取某個特定的模式，只采用一個結構元素，那么，只有與結構元素形狀、大小完全相同的模式才能被提取，而與此結構元素表示的模式即使有微小差別的其他模式的信息都不能獲取。

解決此問題的一個有效方法之一就是將形態學運算與集合運算結合起來，同時采用多個結構元素，分別對圖像進行運算，然后將運算后的圖像合并起來，即多結構元素形態學運算。

?

（2）???????用遺傳算法選取結構元素

遺傳算法的思想來源于自然界物競天擇、優勝劣汰、適者生存的演化規律和生物進化原理，并引用隨機統計理論而形成，具有高效并行全局優化搜索能力，能有效地解決機器學習中參數的復雜優化和組合優化等難題。

近年來不少國外學者已進行了這方面的探索與研究，Ehrgardt設計了形態濾波的遺傳算法，用于二值圖像的去噪和根據二值紋理特性消除預定目標；Huttumen利用遺傳算法構造了軟式形態濾波器及其參數優化的設計方法，以實現灰度圖像的降噪功能。余農、李予蜀等人用遺傳算法在自然景象的目標檢測與提取方面進行了研究，通過自適應優化訓練使結構元素具有圖像目標的形態結構特征，從而賦予結構元素特定的知識，使形態濾波過程融入特有的智能，以實現對復雜變化的圖像具有良好的濾波性能和穩健的適應能力。其實質是解決濾波器設計中知識獲取和知識精煉的機器學習問題。

?

五?數學形態學存在的問題與進一步的研究方向

數學形態學是一門建立在集論基礎之上的學科，是幾何形狀分析和描述的有力工具。近年來，數學形態學在數字圖像處理、計算機視覺與模式識別等領域中得到了越來越廣泛的應用，漸漸形成了一種新的數字圖像分析方法和理論，引起了國內外相關領域研究人員的廣泛關注。目前，數學形態學存在的問題及研究方向主要集中在以下幾個方面：

（1）????????????形態運算實質上是一種二維卷積運算，當圖像維數較大時，特別是用灰度形態學、軟數學形態學、模糊形態學等方法時，運算速度很慢，因而不適于實時處理。

（2）????????????由于結構元素對形態運算的結果有決定性的作用，所以，需結合實際應用背景和期望合理選擇結構元素的大小與形狀。

（3）?????????????軟數學形態學中關于結構元素核心、軟邊界的定義，及對加權統計次數*的選擇也具有較大的靈活性，應根據圖像拓撲結構合理選擇，沒有統一的設計標準。

（4）???????????為達到最佳的濾波效果，需結合圖像的拓撲特性選擇形態開、閉運算的復合方式。

（5）????????????對模糊形態學，不同的模糊算子會直接影響模糊形態學的定義及其運算結果。

（6）???????????有待進一步將數學形態學與神經網絡、模糊數學結合研究灰度圖像、彩色圖像的處理和分析方法。

（7）????????????有待進一步研究開發形態運算的光學實現及其它硬件實現方法。

（8）????????????有待將形態學與小波、分形等方法結合起來對現有圖像處理方法進行改進，進一步推廣應用。所以如何實現灰度形態學、軟數學形態學、模糊軟數學形態學的快速算法，如何改善形態運算的通用性，增強形態運算的適應性，并結合數學形態學的最新應用進展，將其應用到圖像處理領域，豐富和發展利用數學形態學的圖像處理與分析方法，成為數學形態學今后的發展方向。

?

六?結論

數學形態學對圖像的處理具有直觀上的簡明性和數學上的嚴謹性，在定量描述圖像的形態特征上具有獨特的優勢，為基于形狀細節進行圖像處理提供了強有力的手段。建立在集合理論基礎上的數學形態學，主要通過選擇相應的結構元素采用膨脹、腐蝕、開啟、閉合#種基本運算的組合來處理圖像。數學形態學在圖像處理中的應用廣泛，有許多實用的算法，但在每種算法中結構元素的選取都是一個重要的問題。

用3x3的結構元素，掃描圖像的每一個像素，用結構元素與其覆蓋的二值圖像做“與”操作：如果都為1，結果圖像的該像素為1。否則為0。
結果：使二值圖像減小一圈
定義：E = B ? S = { x,y | Sxy?B}膨脹的算法：
用3x3的結構元素，掃描圖像的每一個像素，用結構元素與其覆蓋的二值圖像做“與”操作：如果都為0，結果圖像的該像素為0。否則為1
結果：使二值圖像擴大一圈
定義：E = B ? S = { x,y | Sxy∩B ≠Ф}

一般先將處理圖像轉為整型或邏輯型再處理即可。