受限玻爾茲曼機（RBM）以及對比散度（CD）

1. RBM 的提出

BM 的缺點：

• 計算時間漫長，尤其是無約束自由迭代的負向階段；
• 對抽樣噪音敏感；
• 流行軟件的不支持；

受限玻爾茲曼機（Restricted Boltzmann Machine,簡稱 RBM，以解決 BM 的學習效率過慢的嚴重缺陷）是由 Hinton 和 Sejnowski 于 1986 年提出的一種生成式隨機神經網絡（generative stochastic neural network），該網絡由一些可見單元(visible unit，對應可見變量，亦即數據樣本)和一些隱藏單元(hidden unit，對應隱藏變量)構成，可見變量和隱藏變量都是二元變量，亦即其狀態取{0,1}。整個網絡是一個二部圖，只有可見單元和隱藏單元之間才會存在邊，可見單元之間以及隱藏單元之間都不會有邊連接，如下圖所示：

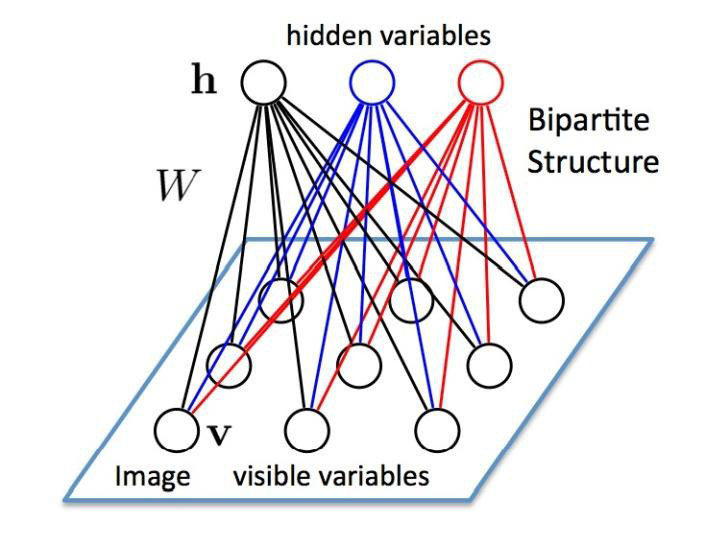
2. BM 與 RBM 的對比

• RBM 和 BM 一樣，都可視為一種無向圖（undirected graph），所謂無向的涵義即在于，權值對稱，wji=wij（自然對于有向圖而言，與指向有關；）

• RBM 同層節點之間沒有連接（BM 有連接），

  • 可見層，隱層：結點之間彼此獨立（簡化的思路）（條件獨立假設），

3. 數學記號

• 能量函數的定義：

  E(v,h|θ)=?∑iaivi?∑jbjhj?∑in∑jmaiWijbj
  • 顯然可以將上述公式簡化為：一種向量的記法；
  • ai：可見層的偏置（bias）
  • bj：隱層的偏置（bias）
  • 豎線右邊的 θ 就像條件概率的形式一樣，一般理解為固定 θ（θ={Wij,ai,bj}）的條件下，E 關于 v,h 的函數；

• v,h 的聯合概率分布為（由玻爾茲曼分布而來）：

  P(v,h)=e?E(v,h|θ)Z(θ)

  Z 十分難計算（2n+m 種組合）

4. CD 算法

θ?=argmaxL(θ)=argmax∑t=1TlogP(v(t)|θ)

目標函數，即在參數（θ）確定的情況，最大化重現（再現）輸入；

5. AE 與 RBM

• AE：
  
  • 出于簡化的考慮：輸入層，隱層，輸出層；
  • 因為通過低維的隱層，可以重構出輸出層，可見低維的隱層，是一種對輸入本質特征的描述，又可從側面說明，輸入層是可以被壓縮，也即存在冗余，進一步我們可認為其是可以被稀疏表示的；
    
    • 平方損失，BP反向傳播，
• RBM：
  
  • 可見層，隱層，可見層，隱層 ,,, ，是一種橫向的展開；
  • 這種周期性的循環結構可以被視為：不同的可見層其實是相互重疊的；
  • 可見層既作為輸入，也作為輸出，（之所以稱其為可見層，隱層，而不是輸入層，隱層，輸出層，就在于，可見層既作為輸入層，也作為輸出層） -