- 概述
在SLAM中,機器人位姿和地圖都是狀態變量,我們需要同時對這兩個狀態變量進行估計,即機器人獲得一張環境地圖的同時確定自己相對于該地圖的位置。我們用x表示機器人狀態,m表示環境地圖,z表示傳感器觀測情況,u表示輸入控制,下標表示時刻,則對
進行估計。而由條件貝葉斯法則,可以得到
這一分解相當于把SLAM分離為定位和構建地圖兩步,大大降低的SLAM問題的復雜度。基于此,Gmaping算法的大致過程為用上一時刻的地圖和運動模型預測當前時刻的位姿,然后根據傳感器觀測值計算權重,重采樣,更新粒子的地圖,如此往復。ROS中實現的Gmapping算法框架大致如下,后面講述原理時將說明對應的代碼模塊:

- 定位
Gmapping算法基于粒子濾波,因此定位部分和粒子濾波大致相同:粒子狀態預測,測量,更新,重采樣。接下來分別說明:
1、狀態預測(draw from motion)
??當前時刻粒子的狀態首先由運動模型進行更新,在初始值上增加高斯采樣的噪聲,進行一個粗略狀態估計。

??在Gmapping算法中,則采用以下算法對運動進行采樣:

2、測量(scan match)
??? 這一步是在粗略估計的基礎上做一次掃描匹配,找到一個使當前觀測最貼合地圖的位姿,以改進基于里程計模型的提議分布。基本思路是在基于運動模型預測的位姿,向負x,正x,負y,正y,左旋轉,右旋轉一共六個狀態移動預測位姿,計算每個狀態下的匹配得分,選擇最高得分對應的位姿為最優位姿。
掃描匹配的重點就在于如何計算匹配得分。所謂匹配,是將當前采集的激光數據與環境地圖進行對準:1)激光點的坐標轉換至網格地圖坐標;2)分別處理六個狀態:當確定激光點網格坐標的地圖值為障礙物時,進行打分(原理與NDT類似,距離越小,分數越大);3)得分最高的位姿為最優位姿。

?? 獲得最優粒子位姿后,可以把粒子采樣范圍從又扁又寬的區域更改到激光雷達觀測模型所代表的尖峰區域L,新的粒子分布就可以更貼近于真實分布。

???? 掃描匹配之后,我們就找到了L所代表的尖峰區域,接下來的任務是確定
該尖峰區域所代表的高斯分布的均值和方差。作者的方法是,在L中隨機采樣K個點,根據這K個點的里程計和觀測模型計算均值和方差,如下式所示。

3、計算權重
???? 然后,對于每個粒子,我們需要計算它的權重,以供后續的重采樣步驟使用。由于在前面我們利用激光數據對提議分布進行了優化:

???? 那么粒子的權重公式變成了:

??? 這里還有一個問題就是權重計算,權重描述的是目標分布和提議分布之間的差別。因此我們在計算權重時就是計算我們模擬出的提議分布和目標分布的不同。而這種不同體現在我們是由有限的采樣模擬出目標分布,因此權重的計算公式為:

4、重采樣(update Tree Weights)
??? 在執行重采樣之前計算了每個粒子的權重,有時會因為環境相似度高或是由于測量噪聲的影響會使接近正確狀態的粒子數權重較小而錯誤狀態的粒子的權重反而會大。重采樣是依據粒子權重來重新采粒子的,這樣正確的粒子就很有可能會被丟棄,頻繁的重采樣更加劇了正確但權重較小粒子被丟棄的可能性。
Gmapping算法中,作者采用權重值離差的量度進行重采樣的判定。
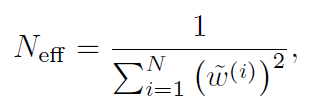
Neff越大,粒子權重差距越小。想象極端情況,當所有粒子權重都一樣的時候(比如重采樣之后),這些粒子恰好可以表示真實分布(類似于按照某個分布隨機采樣的結果)。當Neff降低到某個閾值以下,說明粒子的分布與真實分布差距很大,在粒子層面表現為某些粒子離真實值很近,而很多粒子離真實值較遠,這時候恰好進行重采樣。
- 建圖
Gmapping算法會構建一個柵格地圖,對二維環境進行了柵格尺度劃分,而假設每一個柵格的狀態是獨立的。
對于環境中的一個點,我們用![]() 來表示它是Free狀態的概率,用
來表示它是Free狀態的概率,用![]() 來表示它是Occupied狀態的概率,當然兩者的和為1。為了更方便的表示,我們用
來表示它是Occupied狀態的概率,當然兩者的和為1。為了更方便的表示,我們用![]() 作為該點的狀態,比值越大說明該點約可能是障礙物。
作為該點的狀態,比值越大說明該點約可能是障礙物。
對于一個點,對于一個點,新來了一個測量值z之后我們需要更新它的狀態。假設測量值來之前,該點的狀態為![]() ,我們要更新它為:
,我們要更新它為:
![]() 。
。
由貝葉斯公式計算可得:

為了方便計算,我們對兩邊取對數:
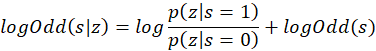
在沒有任何測量值的初始狀態下,一個點的初始狀態為0,而這一部分關鍵的地方在于![]() 的計算,我們稱這個比值為測量值的模型,標記為lomeas。實際上測量值的模型只有兩種:
的計算,我們稱這個比值為測量值的模型,標記為lomeas。實際上測量值的模型只有兩種:![]() 和
和![]() ?,而且都是定值。這樣每獲得一次測量值,我們都能用加減法對點狀態進行更新。從而完成更新地圖的工作。以下圖為例:
?,而且都是定值。這樣每獲得一次測量值,我們都能用加減法對點狀態進行更新。從而完成更新地圖的工作。以下圖為例:

x是真實世界中的坐標,![]() 為柵格地圖中的坐標,r為一格的長度,1/r表示分辨率,則
為柵格地圖中的坐標,r為一格的長度,1/r表示分辨率,則![]() 。則二維情況下:
。則二維情況下:![]() 。假設圖中機器人的位姿為(x,y,
。假設圖中機器人的位姿為(x,y,![]() ),我們可以很容易計算障礙物的位置:
),我們可以很容易計算障礙物的位置:
![]()
其中,d為測量得到的距離,![]() 為激光線與機器人位姿角的夾角。我們得到兩個坐標后能計算出兩點在柵格地圖的位置(i,j )與(
為激光線與機器人位姿角的夾角。我們得到兩個坐標后能計算出兩點在柵格地圖的位置(i,j )與(![]() )。
)。
然后,我們利用bresenham算法(compute active area)來計算非障礙物格點的集合。然后利用上文所述結論,更新柵格地圖即可。

Bresenham算法基本思想是采用遞推步進的辦法,令每次最大變化方向的坐標步進一個像素,同時另一個方向的坐標依據誤差判別式的符號來決定是否也要步進一個像素。舉例說明:

由于顯示直線的象素點只能取整數值坐標,可以假設直線上第i個像素點坐標為(xi,yi),它是直線上點(xi,yi)的最佳近似,并且xi=xi(假設直線斜率小于1)。那么,直線上下一個像素點的可能位置是(xi+1,yi)或(xi+1,yi+1)。由圖中可以知道,在x=xi+1處,直線上點的y值是y=m(xi+1)+b,該點離像素點(xi+1,yi)和像素點(xi+1,yi+1)的距離分別是d1和d2:?
![]()
![]()
這兩個距離差是
![]()
分析d1-d2,有以下三種情況:
- 當此值為正時,d1>d2,說明直線上理論點離(xi+1,yi+1) 像素較近,下一個像素點應取(xi+1,yi+1)。
- 當此值為負時,d1<d2,說明直線上理論點離(xi+1,yi) 像素較近,則下一個像素點應取(xi+1,yi)。
- 當此值為零時,說明直線上理論點離上、下兩個像素點的距離相等,取哪個點都行,算法規定這種情況下取(xi+1,yi+1)作為下一個像素點。
因此只要利用(d1-d2)的符號就可以決定下一個像素點的選擇。
參考文獻
- https://blog.csdn.net/qq_36355662/article/details/90301219
- https://blog.csdn.net/shixiaolu63/article/details/93739379
- https://www.jianshu.com/p/f044da681454
- https://blog.csdn.net/liuyanpeng12333/article/details/81946841
- https://www.cnblogs.com/yhlx125/p/5634128.html
- 概率機器人
- 粒子濾波:從推導到應用
- Improved Techniques for Grid Mapping with Rao-Blackwellized Particle Filters
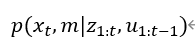









![[TOOLS] 移動端調試進行時 - whistle](http://pic.xiahunao.cn/[TOOLS] 移動端調試進行時 - whistle)




)




