????????圖像降噪處理主要分為2D（空域）與3D降噪（時域/多幀），而2D降噪由于相關的實現算法豐富，效果各異，有著豐富的研究價值。理解2D降噪算法的流程，也對其他的增強算法有很大的幫助，本文將介紹均值濾波到非局部均值濾波算法的原理及實現方式。

????????細數主要的2D降噪算法，如下圖所示，從最基本的均值濾波到相對最好的BM3D降噪，本文將詳解這些算法的實現流程，并給予一定的FPGA加速實現的實現思路。

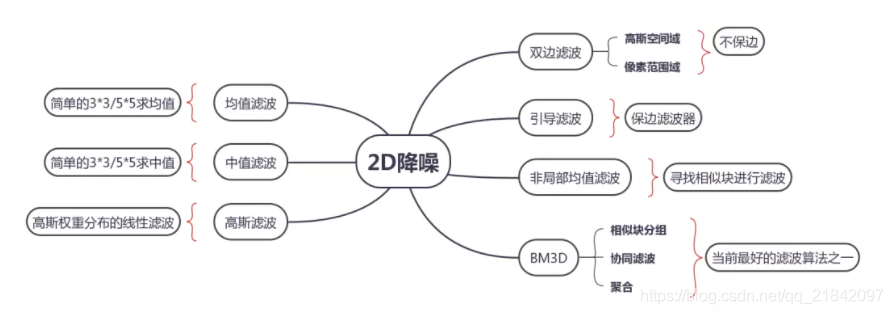
一、均值/中值濾波

? ? ? ? 現所有濾波算法都是通過當前像素周邊的像素，以一定的權重來計算濾波的像素值。因此主要涉及兩個變量：窗口的大小，以及窗口內像素的權重。以最簡單的均值濾波/中值濾波，3*3窗口為例，計算及優缺點如下：

均值濾波? ? ? ??

????????對于FPGA的硬件加速實現，過程還好，唯一頭疼的就是涉及了除法，由于除法計算時鐘周期長且耗費LE，我們需要升級改造下，因此優化公式如下（sum為9個像素累加的結果），將除法巧妙變成乘法：

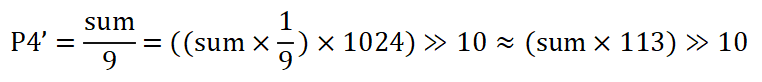
因此實現的流程如下

1）sum1=P0+P1+P2; sum2=P3+P4+P5; sum3=P6+P7+P8，即先求每行3像素累加

2）sum=sum1+sum2+sum3，即求三行9像素累加

3）sum*144，取結果的[17:10]，即為均值濾波的結果。

4）以上過程流水線，最終每個clk輸出一個計算結果。

備注：這里1024/9取了floor，這樣保證不會溢出。

中值濾波

對于中值濾波而言，本身計算并不復雜，就看怎么取巧最快得到中間數，網上流傳了一個三步法，即如下圖所示，

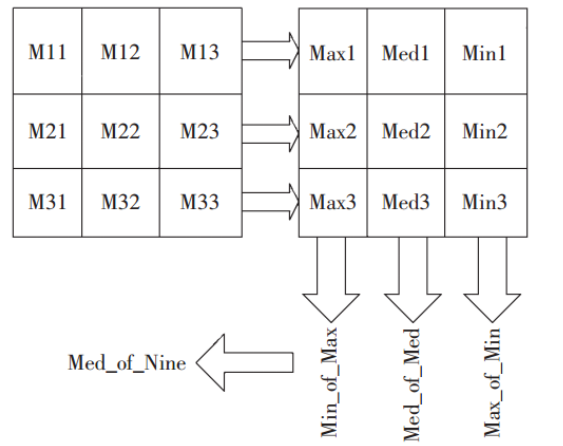
那么FPGA硬件加速實現，流程如下：

1）計算每行3個像素的最大中、中值、最小值

2）計算三個最大值的最小值，中間值的中間值，以及最小值的最大值。

3）對上述三個值求得中間值。

4）以上過程流水線，最終每個clk輸出一個計算結果。

中值濾波計算相對均值濾波稍微復雜一點，但是好處是只用了比較器，沒用乘法器，比均值濾波更省資源。

對于椒鹽圖像的均值濾波、中值濾波計算效果對比，如下所示，分別為椒鹽圖像、均值濾波、中值濾波結果。

二、高斯濾波

????????前面講的均值/中值濾波，對于窗口內每個像素的權重都是一樣的，噪聲在圖像當中常表現為一引起較強視覺效果的孤立像素點或像素塊，那么他必然不是平均分布。

????????正態分布是最重要的一種概率分布，也叫做高斯分布。在正態分布里，中間狀態是常態，過高和過低都屬于少數，因此正態分布具有相當的普遍性。

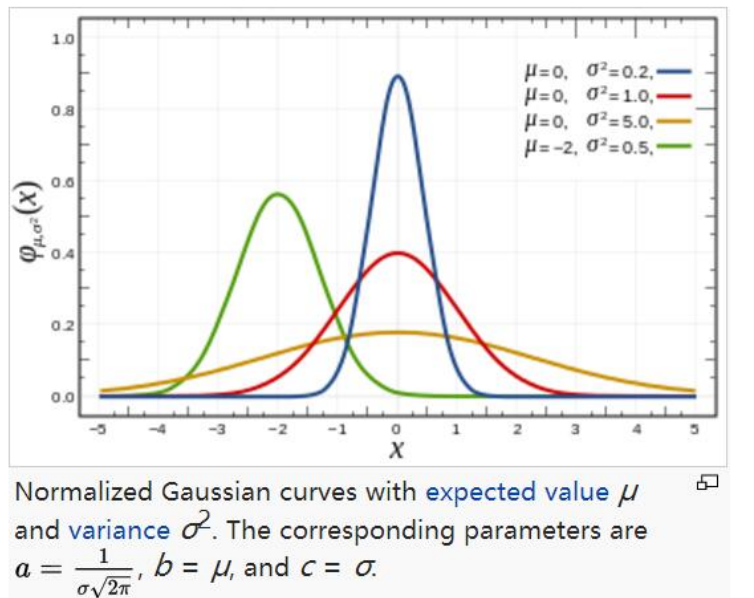
?????????因此以概率論及中心極限定理猜想，大部分噪聲應該也符合正態分布/高斯分布（高斯白噪聲），所以也就有了高斯濾波，及根據正態分布進行權重計算的濾波方法。上圖曲線是高斯分布的一維函數，而圖像應該是二維的，圖解如下二維高斯分布：

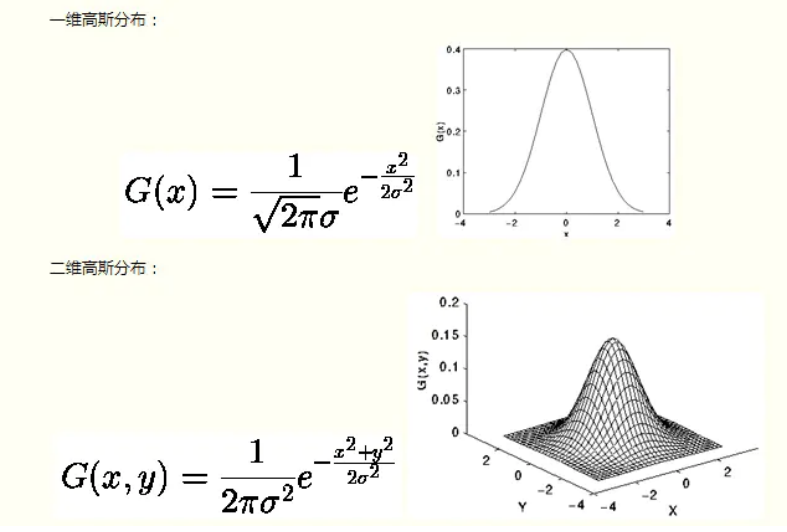
????????既然已經得到二維高斯分布函數，那么根據窗口到目標像素的距離，就可以是計算出周邊像素的權重——高斯模板。均值濾波每個像素的權重都是1/9，再通過卷積后計算得到結構，而高斯濾波就是根據正態分布，去計算當前像素相對距離的權重值，假定σ=1.5（σ就是濾波的強度），3*3的高斯模板計算計算過程如下：

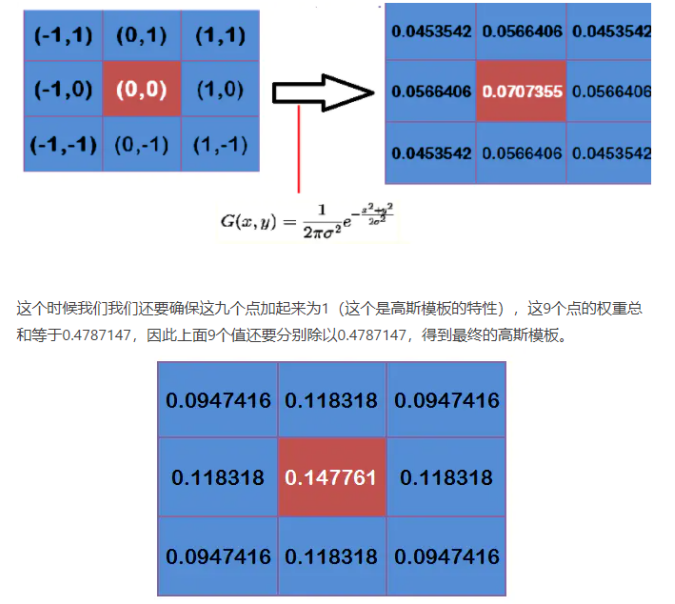
????????但是這還不夠，畢竟我們的目標是直接上FPGA，那必須頂定點化，因此假設擴大1024倍，則3*3的高斯模板定點化如下：

????????對于3*3或者5*5，選定的σ，高斯模板那么，現在計算就簡單了，卷積后再縮小1024倍即可，采用FPGA計算，過程如下：

1）計算9個像素的對應卷積參數的乘法

2）9累加9個乘法結果

3）右移10bit或取結果的[17:10]，即為高斯濾波的結果。

4）以上過程流水線，最終每個clk輸出一個計算結果。

備注：當然實現還可優化，比如只用3個乘法器，算一行累加一行，也就4個時鐘算完。

最后，暫且盜用別人針對不同σ的3*3高斯濾波效果圖，如下（σ越大越模糊）：

?三、雙邊濾波

????????雙邊濾波是一種非線性濾波器，它可以達到保持邊緣、降噪平滑的效果。和其他濾波原理一樣，雙邊濾波也是采用加權平均的方法，用周邊像素亮度值的加權平均代表某個像素的強度，所用的加權平均基于高斯分布。

????????但是，雙邊濾波的權重不僅考慮了像素的歐式距離（如高斯濾波）——核域，還考慮了像素范圍域中的輻射差異（比如像素與中心像素之間相似程度）——值域，計算時同時考慮這兩個權重。?

????????借用上網的一個圖，如上為同時考慮核域與值域的像素濾波計算公式，其中space weight和range weight都符合高斯分布，但前者僅靠了距離，后者考慮了差值，因此兩者結合就是同時考慮了space & range濾波。上述公式太抽象，重新梳理如下（其中1/Wp為歸一化因子）：

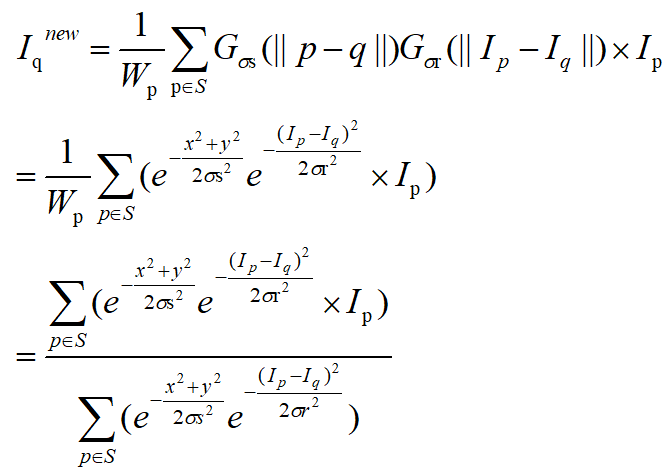
????????由于雙邊濾波同時考慮了空間距離和像素相似度的影響，因此尤其在具有邊緣梯度的圖像中，能夠有不錯的效果。即在平坦區域，空間距離占優勢，在邊緣區域，像素間相似度占優勢，可以直觀的用下面這個圖來表示：

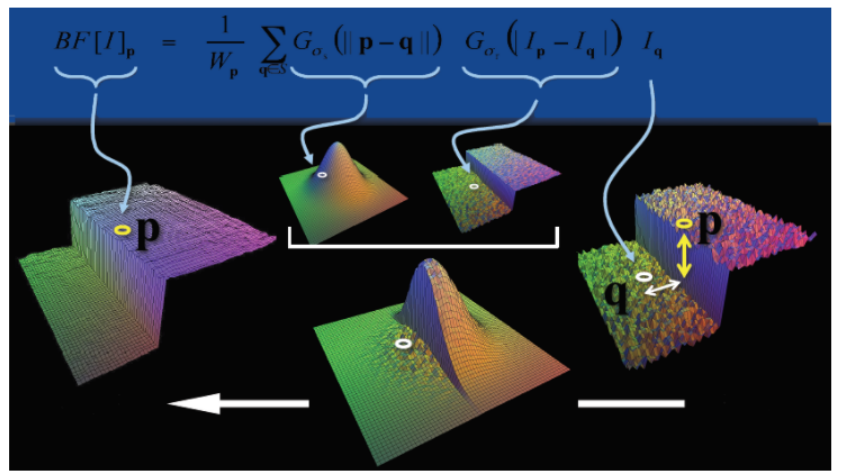
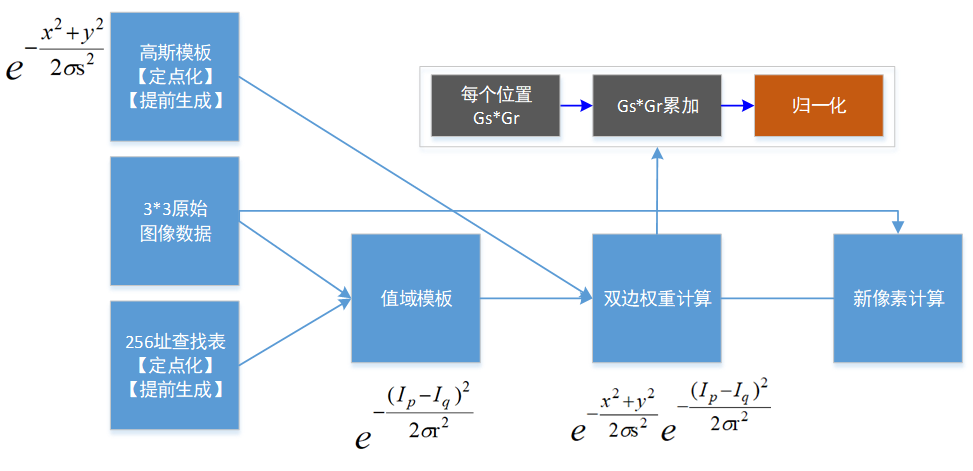
根據上圖，繼續進一步細化步驟，詳解在FPGA中的實現方式，如下：

1）提前計算好高斯模板，和用于值域權重計算的256地址數據（均已擴大1024倍定點化）

2）根據3*3原圖和中心點差值判斷，得到值域模板

3）將提前準備的高斯模板和上一步的值域模板相乘，得到雙邊權重模板

4）將得到的3*3個新的權重累加，

5）根據累加結果，歸一化（歸1024化）完成最終權重模板的計算

6）最新模板和原始3*3原圖卷積，得到新的目標像素。

7）以上過程流水線，最終每個clk輸出一個計算結果。

OK，搞定，巧妙使用1024倍定點化，及查找表的方法，所有指數相關操作全部解決，在允許的誤差范圍內，實現FPGA的加速運算。

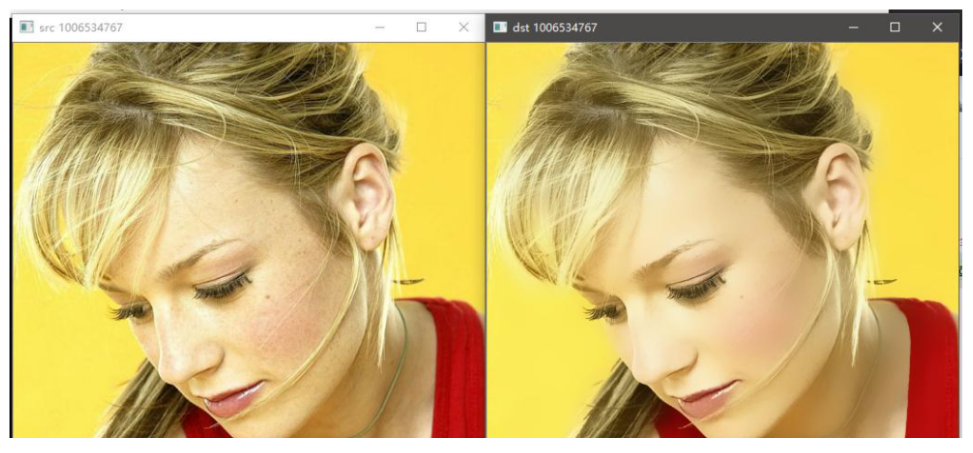
雙邊濾波其實就是個磨皮算法，用于美容養顏還是不錯，所以網上找了一個圖給大家參考下，如此下：

????但是，這里的歸一化還是有不盡人意的地方，因為不確定9個權重累加的值是多少，因此無法采用乘法來替代除法，這一塊暫且在后面想好了再追加討論。

參考文章

1. https://blog.csdn.net/qinghuaci666/article/details/81737624
2. https://www.cnblogs.com/yoyo-sincerely/p/6058944.html
3. https://www.jianshu.com/p/73e6ccbd8f3f
4. https://blog.csdn.net/abcjennifer/article/details/7616663
5. https://blog.csdn.net/u013066730/article/details/87859184