洛谷 P2296 尋找道路

題目描述

在有向圖G 中，每條邊的長度均為1 ，現給定起點和終點，請你在圖中找一條從起點到終點的路徑，該路徑滿足以下條件：

1 ．路徑上的所有點的出邊所指向的點都直接或間接與終點連通。

2 ．在滿足條件1 的情況下使路徑最短。

注意：圖G 中可能存在重邊和自環，題目保證終點沒有出邊。

請你輸出符合條件的路徑的長度。

輸入輸出格式

輸入格式：

?

輸入文件名為road .in。

第一行有兩個用一個空格隔開的整數n 和m ，表示圖有n 個點和m 條邊。

接下來的m 行每行2 個整數x 、y ，之間用一個空格隔開，表示有一條邊從點x 指向點y 。

最后一行有兩個用一個空格隔開的整數s 、t ，表示起點為s ，終點為t 。

?

輸出格式：

?

輸出文件名為road .out 。

輸出只有一行，包含一個整數，表示滿足題目?述的最短路徑的長度。如果這樣的路徑不存在，輸出- 1 。

?

輸入輸出樣例

輸入樣例#1：

3 2  
1 2  
2 1  
1 3  

輸出樣例#1：

-1

輸入樣例#2：

6 6  
1 2  
1 3  
2 6  
2 5  
4 5  
3 4  
1 5  

輸出樣例#2：

3

說明

解釋1：

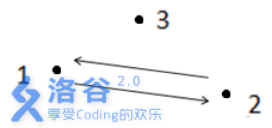
如上圖所示，箭頭表示有向道路，圓點表示城市。起點1 與終點3 不連通，所以滿足題

目?述的路徑不存在，故輸出- 1 。

解釋2：

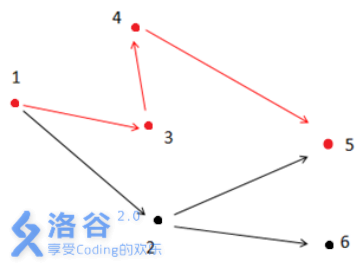
如上圖所示，滿足條件的路徑為1 - >3- >4- >5。注意點2 不能在答案路徑中，因為點2連了一條邊到點6 ，而點6 不與終點5 連通。

對于30%的數據，0<n≤10，0<m≤20；

對于60%的數據，0<n≤100，0<m≤2000；

對于100%的數據，0<n≤10,000，0<m≤200,000，0<x，y，s，t≤n，x≠t。

?

?

正反存邊

反跑dfs標記終點能到達的點 也就是能到達終點的點

然后把出邊不能到達終點的點標記為不能走

然后正跑spfa

屠龍寶刀點擊就送

#include <vector>
#include <cstdio>
#include <queue>
#define N 10005
using namespace std;
vector<int>G1[N],G2[N];
bool cant[N],vis[N];
int n,m,s,t,dis[N];
void dfs(int x)
{vis[x]=1;for(int i=0;i<G2[x].size();++i){int v=G2[x][i];if(!vis[v]) dfs(v);}
}
int main()
{scanf("%d%d",&n,&m);for(int x,y,i=1;i<=m;++i){scanf("%d%d",&x,&y);G1[x].push_back(y);G2[y].push_back(x); }scanf("%d%d",&s,&t);dfs(t);for(int i=1;i<=n;++i){bool flag=false;if(!vis[i]) {cant[i]=1;continue;}for(int j=0;j<G1[i].size();++j){int v=G1[i][j];if(!vis[v]) {flag=1;break;} }if(flag) {cant[i]=1;continue;}}for(int i=1;i<=n;++i) dis[i]=0x3f3f3f3f,vis[i]=0;dis[s]=0;vis[s]=1;queue<int>q;q.push(s);for(int now;!q.empty();){now=q.front();q.pop();vis[now]=0;if(cant[now]) continue;for(int i=0;i<G1[now].size();++i){int v=G1[now][i];if(dis[v]>dis[now]+1){dis[v]=dis[now]+1;if(!vis[v]){q.push(v);vis[v]=1; }}}}dis[t]==0x3f3f3f3f?printf("-1"):printf("%d",dis[t]);return 0;
}

?