排序

參考：https://www.bilibili.com/video/av38482633/?spm_id_from=trigger_reload

排序

插入排序

直接插入排序

折半排序

希爾排序

交換排序

冒泡排序

快速排序

?選擇排序

堆排序

流量單位計算

什么是計數排序

復雜度分析：

什么是基數排序？

復雜度分析（原始數列的規模是N,最大最小整數的差值是M）

插入排序

（有序插入，在有序序列中插入一個元素，保持序列有序，有序長度增加）

直接插入排序

——零號位為哨兵，i位要排序，順序查找j，依次比較哨兵，大則j往后移覆蓋，否則原地不動，i賦值j+1（比較后單向移動，不是交換）

折半排序

（循環比較mid=（low+height）/ 2? 與哨兵位置的大小，如果哨兵小，則到左半區查找，height=mid-1，否則右半區low=mid+1，直至low大于height，確定插入位置，然后將插入位置后面的所有對象都往后移動位置，將哨兵插入height+1）

希爾排序

（算法是一步一步來的，兩兩對比，相隔n個數據，然后模仿直接插入排序，完事兒后接著下一個數據接著同樣的以上來插入排序，最后一個間隔數值一定是1）

交換排序

冒泡排序

（基于簡單的交換思想，兩兩比較，大的沉底，前小后大，需要一個臨時空間暫存交換操作中的元素）

如果發現一次排序后沒有交換數據，那咋說明前排的數據都是有序的了，不需要再冒泡排序了

快速排序

（改進的交換排序，取中點放捎點，low、hign指針比較捎點大小分為左右區域，之后左右區域遞歸，不穩定）

?選擇排序

簡單選擇排序（選擇未排序里最小的并與第一個進行交換，之后依次步驟一樣）

堆排序

無序的話就按數組順序，由根往下排，并從第一個非葉子節點（n/2 | 0）開始堆調整，直至符合堆的定義

流量單位計算

流量單位G,M,K,B,是什么意思？
G, M, K, B, 都是數據或數據流量的單位符號。
其中，B 是字節的符號，字節是數據或數據流量的基本單位。
它們之間的換算關系是：

什么是計數排序

先考一道算法題:

數組里有20個隨機整數，取值范圉從0到10，要求用最快的速度把這20個整數從小到大進行排序。有沒有比快速排序 0（ nlogn）更快的排序方法呢？有的，就是用計數排序。

讓我們先來回顧一下咱們以前所學過的排序算法，無論是冒泡排序，還是快速排序等等，都是基于元素之間的比較來進行排序。有一種特殊的排序算法叫做【計數排序】，這種排序算法不是基于元素比較，而是利用數組下標來確定元素的正確位置。

基于上題中，整數的取值范圍只是從0-10之間，讓我們根據這個整數取值范圍，建立一個長度為11的數組。數組下標從0到10，元素初始值全為0。

假定20個隨機整數的值如下

9，3，5，4，9，1，2，7，8，1，3，6，5，3，4，0，10，9，7，9

如何給這些無序的隨機整數排序呢？

非常簡單，讓我們遍歷這個無序的隨機數列，每一個整數按照其值對號入座，對應數組下標的元素進行加1操作。

比如第一個整數是9，那么數組下標為9的元素加1:

第二個整數是3，那么數組下標為3的元素加1:

最終，數列遍歷完畢時，數組的狀態如下

數組每一個下標位置的值，代表了數列中對應整數出現的次數

有了這個“統計結果”，排序就很簡單了。直接遍歷數組，輸出數組元素的下標值，

元素的值是幾，就輸出幾次

0，1，1，2，3，3，3，4，4，5，5，6，7，7，8，9，9，9，9，10

顯然，這個輸出的數列已經是有序的了。

這就是計數排序的基本過程，它適用于一定范圍的整數排序。在取值范圍不是很大的情況下，它的性能甚至快過那些0(nlogn)的排序。

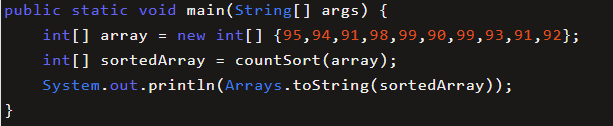
初步代碼如下：

這段代碼在一開頭補充了一一個步驟,就是求得數列的最大整數值max。后面創建的統計數組countArray ,長度就是max+1 ,以此保證數組的最后-一個下標是max。

只以數列的最大值來決定統計數組的長度，其實并不嚴謹。而應該以最大值和最小值的差來作為數組的大小。不然會浪費空間。

我們不再以(輸入數列的最大值+1 )作為統計數組的長度,而是以(數列最大值和最小值的差+1 )作為統計數組的長度。同時,數列的最小值作為-一個偏移量,用于統計數組的對號入座。

以這個數列為例,統計數組的長度為99-90+1 = 10 , 偏移量等于數列的最小值90。對于第一個整數95 ,對應的統計數組下標是95-90 = 5 ,如圖所示:

此外，樸素版的計數排序只是簡單地按照統計數組的下標輸出了元素值，并沒有真正給原始數列進行排序。

如果是單純的給整數排序，這樣并沒有問題。但如果放在現實業務里,比如給學生的考試分數排序，遇到相同的分數就會分不清誰是誰。
?

給定一個學生的成績表,要求按成績從低到高排序,如果成績相同,則遵循原表固有順序。
那么,當我們填充統計數組以后,我們只知道有兩個成績并列95分的小伙伴,卻不知道哪一個是小紅，哪一一個是小綠:
我們需要稍微改變之前的邏輯,在填充完統計數組以后，對統計數組做一下變形。

統計數組從第二個元素開始，每一個元素都加上前面所有元素之和。

這樣相加的目的，是讓統計數組存儲的元素值，等于相應整數的最終排序位置。比如下標是9的元素值為5，代表原始數列的整數9，最終的排序是在第5位。

接下來，我們創建輸出數組sortedArray，長度和輸入數列一致。然后從后向前遍歷輸入數列：

第一步，我們遍歷成績表最后一行的小綠：

小綠是95分，我們找到countArray下標是5的元素，值是4，代表小綠的成績排名位置在第4位。（位置下標是3，因為成績最少的是第一位，而他下標的位置對應就是0）

同時，我們給countArray下標是5的元素值減1，從4變成3,，代表著下次再遇到95分的成績時，最終排名是第3。

這樣一來，同樣是95分的小紅和小綠就能夠清楚地排出順序了，也正因此，優化版本的計數排序屬于穩定排序。

復雜度分析：

如果原始數列的規模是N,最大最小整數的差值是M,你說說計數排序的時間復雜度和空間復雜度是多少?
代碼第1, 2, 4步都涉及到遍歷原始數列，運算量都是N,第3步遍歷統計數列,運算量是M，所以總體運算量是3N+M,去掉系數，時間復雜度是0 (N+M)。
至于空間復雜度，如果不考慮結果數組，只考慮統計數組大小的話,空間復雜度是0 (M) 。
而計數排序存在它的局限性，主要表現在兩點:

1.當數列最大最小值差距過大時，并不適用計數排序。

比如給定20個隨機整數，范圍在0到1億之間，這時候如果使用計數排序，需要創建長度1億的數組。不但嚴重浪費空間，而且時間復雜度也隨之升高。

2.當數列元素不是整數，并不適用計數排序。

如果數列中的元素都是小數，比如25.213，或是0.00000001這樣子，則無法創建對應的統計數組。這樣顯然無法進行計數排序。

對于這些局限性，另一種線性時間排序算法做出了彌補，這種排序算法叫做[桶排序]，我們后續將會講到。
參考：?什么是計數排序？

什么是基數排序？

讓我們接著來看兩個特殊的需求：

需求 A，為一組給定的手機號排序：

18914021920

13223132981

13566632981

13660891039

13361323035

........

按照計數排序的思路，我們要根據手機號的取值范圍，創建一個空數組。

可是，11 位手機號有多少種組合？恐怕要建立一個大得不可想象的數組，才能裝下所有可能出現的 11 位手機號！

需求 B，為一組英文單詞排序：

banana

apple

orange

peach

cherry

........

計數排序適合的場景是對整數做排序，如果遇到英文單詞，就無能為力了。

如何有效處理諸如手機號、英文單詞等復雜元素的排序呢？僅僅靠一次計數排序很難實現。

這時候，我們不妨把排序工作拆分成多個階段，每一個階段只根據一個字符進行計數排序，一共排序 k 輪（k 是元素長度）。

或許這樣的描述有些抽象，我們來舉一個例子。

數組中有若干個字符串元素，每個字符串元素都是由三個英文字母組成：

bda，cfd，qwe，yui，abc，rrr，uee

如何將這些字符串按照字母順序排序呢？

由于每個字符串的長度是 3 個字符，我們可以把排序工作拆分成 3 輪：

第一輪：按照最低位字符排序。排序過程使用計數排序，把字母的 ascii 碼對應到數組下標，第一輪排序結果如下：

第二輪：在第一輪排序結果的基礎上，按照第二位字符排序。

需要注意的是，這里使用的計數排序必須是穩定排序，這樣才能保證第一輪排出的先后順序在第二輪還能繼續保持。

比如在第一輪排序后，元素 uue 在元素 yui 之前。那么第二輪排序時，兩者的第二位字符雖然同樣是 u，但先后順序萬萬不能變，否則第一輪排序就白做了。

第三輪：在第二輪排序結果的基礎上，按照最高位字符排序。

如此一來，這些字符串的順序就排好了。

像這樣把字符串元素按位拆分，每一位進行一次計數排序的算法，就是基數排序（Radix Sort）。

基數排序既可以從高位優先進行排序（Most Significant Digit first，簡稱MSD），也可以從低位優先進行排序（Least Significant Digit first，簡稱LSD）。

不過，如果排序的字符串長度不規則呢?這個問題不難解決。我們以最長的字符串為準，其他度不足的字符串，在末尾補0即可。在排序時，我們把字符 0 當做是比 a 更小的字符，排序結果如下：

ape000

apple0

banana

he0000

orange

代碼如下：

備注：

ASCII ((American Standard Code for Information Interchange): 美國信息交換標準代碼）是基于拉丁字母的一套電腦編碼系統，主要用于顯示現代英語和其他西歐語言。它是最通用的信息交換標準，并等同于國際標準ISO/IEC 646。ASCII到目前為止共定義了128個字符??。

空字符的ASCII碼如下：