https://blog.csdn.net/hustqb/article/details/77922031
-
- 評分參數定義模型評價規則
- 公共案例預定義值
- 根據度量函數定義你的評分策略
- 應用你自己的評分對象
- 使用多種度量指標
- 分類度量
- 從二分類到多分類多標簽
- 精確度
- Cohens kappa
- 混亂矩陣
- 分類報告
- 漢明損失
- Jaccard 相似性相關系數
- 準確率召回率和F度量
- 二分類
- 多分類多標簽
- Hinge損失
- Log損失
- Matthews 相關系數
- ROC
- 0-1損失
- Brier score損失
- 多標簽分級度量
- Coverage誤差
- 分級標簽平均準確度
- 分級損失
- 回歸度量
- Explained variance score
- 均值絕對誤差
- 均值平方誤差
- 均值平方對數誤差
- 中位數絕對誤差
- R2R2 score定義相關性
- 聚類度量
- 簡陋評分器
- 評分參數定義模型評價規則
?
在sklearn庫里,用于評估模型預測的質量的API一共有3種:
- 評分方法:評估者具有
score(),面向其要解決的問題,可以提供一個默認評估標準。 這部分內容不在本文中講述,因為它因不同的模型而異,所以會在各個模型的介紹文檔中講述。 - 評分參數:使用交叉驗證的模型評估工具(如
model_selection.cross_val_score和model_selection.GridSearchCV)依賴于內部評分策略。這些內容會在其他章節(評分參數:定義模型評判規則)中討論。 - 度量函數:
metrics模塊實現了針對特定目的評估誤差的功能。 這些指標會在下面這些章節詳細介紹:Classification metrics,?Multilabel ranking metrics,?Regression metrics?and?Clustering metrics.?
最后,Dummy estimators對于獲得隨機預測的這些指標的基準值是有用的。
聲明:
- 本文譯自Python庫sklearn里的官方文檔
- 需要讀者對Python有一定的了解
- 本文超長…而且因為水平有限,有些地方翻譯的較為生硬。
評分參數:定義模型評價規則
??模型選擇和評估通常使用工具(比如model_selection.GridSearchCV和model_selection.cross_val_score),使用一個scoring參數控制那個被我們應用在我們的評價系統的度量方法。
公共案例:預定義值
??對于最常見的用例,您可以指定一些自帶scoring參數的評分對象; 下表顯示了所有可能的值。 所有得分手對象遵循慣例:返回值越大,分數越高,模型越優。 因此,衡量模型和數據之間距離的度量(如metrics.mean_squared_error)可以用它們的負值作為評分對象的返回值。
| Scoring | Function | Comment |
|---|---|---|
| 分類 | ? | ? |
| ‘accuracy’ | metrics.accuracy_score | ? |
| ‘average_precision’ | metrics.average_precision_score | ? |
| ‘f1’ | metrics.f1_score | ? |
| ‘f1_micro’ | metrics.f1_score | ? |
| f1_macro’ | metrics.f1_score | ? |
| ‘f1_weighted’ | metrics.f1_score | ? |
| ‘f1_samples’ | metrics.f1_score | ? |
| ‘neg_log_loss’ | metrics.log_loss | ? |
| ‘precision’ etc | metrics.precision_score | ? |
| ‘recall’ etc | metrics.recall_score | ? |
| ‘roc_auc’ | metrics.roc_aur_score | ? |
| 聚類 | ? | ? |
| ‘adjusted_mutual_info_score’ | metrics.adjusted_mutual_info_score | ? |
| ‘adjusted_rand_score’ | metrics.adjusted_rand_score | ? |
| ‘completeness_score’ | metrics.completeness_score | ? |
| ‘fowlkes_mallow | s_score’ | metrics.fowlkes_mallows_score |
| ‘homogeneity_score’ | metrics.homogeneity_score | ? |
| ‘mutual_info_score’ | metrics.mutual_info_score | ? |
| ‘normalized_mutual_info_score’ | metrics.normalized_mutual_info_score | ? |
| ‘v_measure_score’ | metrics.v_measure_score | ? |
| 回歸 | ? | ? |
| ‘explained_variance’ | metrics.explained_variance_score | ? |
| ‘neg_mean_absolute_error’ | metrics.mean_absolute_error | ? |
| ‘neg_mean_squared_error’ | metrics.mean_squared_error | ? |
| ‘neg_mean_squared_log_error’ | metrics.mean_squared_log_error | ? |
| ‘neg_median_absolute_error’ | metrics.median_absolute_error | ? |
| ‘r2’ | metrics.r2_score | ? |
例子:
from sklearn import svm, datasets # 導入SVM模型庫和數據集庫
from sklearn.model_selection import cross_val_score # 導入模型選擇庫中的交叉驗證分數函數'''加載鳶尾花數據集'''
iris = datasets.load_iris()
X, y = iris.data, iris.target
clf = svm.SVC(probability=True, random_state=0) # 創建SVC分類器
'''輸出分類器的評分''' score_arr = cross_val_score(clf, X, y, scoring='neg_log_loss') print score_arr # 輸出 [-0.0757138 -0.16816241 -0.07091847] print score_arr.shape # 輸出 (3L,) model = svm.SVC() # 在創建一個SVC分類器 '''應用另一種不存在的評分方式''' cross_val_score(model, X, y, scoring='wrong_choice') # 會報錯ValueError
PS:ValueError異常列出的值對應于以下部分中描述的測量預測精度的函數。 這些評分對象存儲在字典sklearn.metrics.SCORERS中。
根據度量函數定義你的評分策略
??模塊sklearn.metrics還展示了一組測量預測誤差(給出了真實值和預測值)的簡單函數:
- 以
_score結尾的函數返回值用于最大化,越高越好 - 以
_error或_loss結尾的函數返回一個值用于最小化,越低越好。當使用make_scorer()函數將其轉換為評分對象時,請將greater_is_better參數設置為False(默認為True)。
可用于各種機器學習任務的指標在下面詳細介紹。?
??許多指標不會以scoring為名稱,有時是因為它們需要其他參數,例如fbeta_score。在這種情況下,您需要生成一個適當的scorer對象。生成可評估對象進行評分的最簡單的方法是使用make_scorer()函數。該函數將度量轉換為可用于模型評估的可調用的數據類型(callable)。?
??一個典型的用例是使用無默認值的參數轉換包裝庫中已存在的度量函數,例如fbeta_score()函數的beta參數:
from sklearn.metrics import fbeta_score, make_scorer # 導入fbeta評分函數和一個轉換函數
ftwo_scorer = make_scorer(fbeta_score, beta=2) # 通過make_scorer創建新方法 from sklearn.model_selection import GridSearchCV from sklearn.svm import LinearSVC '''待評價的分類模型是線性SVC,超參數域為{1, 10}, 評分方法為前面新轉換的方法''' grid = GridSearchCV(LinearSVC(), param_grid={'C': [1, 10]}, scoring=ftwo_scorer)??第二個用例是使用make_scorer將一個簡單的python函數構建一個完全自定義的scorer對象,它可以使用幾個參數:
- 你要使用的python函數(在下面的示例中為
my_custom_loss_func()) - 明確python函數是否返回一個分數(
greater_is_better = True,默認值)或一個損失值(greater_is_better= False)。 如果一個損失,得分器對象的python函數的輸出被取負值以符合交叉驗證慣例,更優的模型返回更高的值。 - 僅用于分類度量的時候:判斷您提供的python函數是否需要連續性判斷(
needs_threshold = True)。 默認值為False。 - 任何其他參數,如
f1_score()函數中的參數:beta和labels。
以下是建立自定義scorer,以及使用greater_is_better參數的示例:
import numpy as np
def my_custom_loss_func(ground_truth, predictions): """ 自定義損失函數——其實就是典型的SVM損失函數 groud_truth: 真實值 predictions: 預測值 """ diff = np.abs(ground_truth - predictions).max() return np.log(1 + diff)loss = make_scorer(my_custom_loss_func, greater_is_better=False) # 創建為scorer
score = make_scorer(my_custom_loss_func, greater_is_better=True)
ground_truth = [[1], [1]]
predictions = [0, 1]
from sklearn.dummy import DummyClassifier
clf = DummyClassifier(strategy='most_frequent', random_state=0) # 創建簡陋分類模型 clf = clf.fit(ground_truth, predictions) # 訓練模型 loss(clf,ground_truth, predictions) # 損失值,False:取負 score(clf,ground_truth, predictions) # 評分, True:取正這個代碼是沒有實際意義的,只是為了體現兩點
- 自定義評分函數時,需要用到真實值和預測值,然后根據自己的想法輸出預測的誤差或者分值,這里輸出的是誤差。
make_scorer()函數的參數greater_is_better是為了適應靈活的自定義評分函數的。當你的評分函數輸出損失值的時候,參數為False,即對損失值取負;輸出分值的時候,反之。這都是為了遵從前面所說的越大越優的慣例。
應用你自己的評分對象
??您可以通從頭開始構建自己的評分對象,而不使用make_scorer()工廠函數,這樣生成的scorer模型更靈活。 要成為scorer,需要符合以下兩個規則所指定的協議:
- 可以使用參數
(estimator,X,y)調用,其中estimator是應該評估的模型,X是驗證數據,y是X(在監督的情況下)的真實標簽或None(在無監督的情況下)。 - 它返回一個浮點數,用于量化X上的estimator參考y的預測質量。 再次,按照慣例,更高的值表示更好的預測模型,所以如果你的返回的是損失值,應取負。
使用多種度量指標
??Scikit-learn還允許在GridSearchCV,RandomizedSearchCV和cross_validate中使用多個度量指標。為評分參數指定多個評分指標有兩種方法:
- 作為一個包含字符串的迭代器:
scoring = ['accuracy', 'precision']- 作為一個scorer名字到scorer函數的映射:
from sklearn.metrics import accuracy_score
from sklearn.metrics import make_scorer
scoring = {'accuracy': make_scorer(accuracy_score), 'prec': 'precision'}??請注意,字典中的值可以是scorer函數,也可以是一個預定義的度量指標的字符串。目前,只有那些返回單一分數的scorer函數才能在dict內傳遞。 不允許返回多個值的Scorer函數,并且需要一個包裝器才能返回一個度量:
from sklearn.model_selection import cross_validate # 交叉驗證函數
from sklearn.metrics import confusion_matrix X, y = datasets.make_classification(n_classes=2, random_state=0) # 一個簡陋的二分類數據集 svm = LinearSVC(random_state=0) def tp(y_true, y_pred): return confusion_matrix(y_true, y_pred)[0, 0] def tn(y_true, y_pred): return confusion_matrix(y_true, y_pred)[0, 0] def fp(y_true, y_pred): return confusion_matrix(y_true, y_pred)[1, 0] def fn(y_true, y_pred): return confusion_matrix(y_true, y_pred)[0, 1] scoring = {'tp' : make_scorer(tp), 'tn' : make_scorer(tn), 'fp' : make_scorer(fp), 'fn' : make_scorer(fn)} cv_results = cross_validate(svm.fit(X, y), X, y, scoring=scoring) print(cv_results['test_tp']) # 獲取test數據集的tp值 [12 13 15] print(cv_results['test_fn']) # 獲取test數據集的fn值 [5 4 1]?
分類度量
??sklearn.metrics模塊實現了幾種損失函數、評分函數和功能函數來測量分類性能。 某些指標可能需要正例,置信度值或二進制決策值的概率估計。 大多數指標應用的是:通過sample_weight參數,讓每個樣本為總分提供加權貢獻。?
其中一些僅限于二進制分類案例:
| ? |
|---|
| precision_recall_curve(y_true, probas_pred) |
| roc_curve(y_true, y_score[, pos_label, …]) |
還有一些僅限于多分類情形:
| ? |
|---|
| cohen_kappa_score(y1, y2[, labels, weights, …]) |
| confusion_matrix(y_true, y_pred[, labels, …]) |
| hinge_loss(y_true, pred_decision[, labels, …]) |
| matthews_corrcoef(y_true, y_pred[, …]) |
還有一些可用于多標簽情形:
| ? |
|---|
| accuracy_score(y_true, y_pred[, normalize, …]) |
| classification_report(y_true, y_pred[, …]) |
| f1_score(y_true, y_pred[, labels, …]) |
| fbeta_score(y_true, y_pred, beta[, labels, …]) |
| hamming_loss(y_true, y_pred[, labels, …]) |
| jaccard_similarity_score(y_true, y_pred[, …]) |
| log_loss(y_true, y_pred[, eps, normalize, …]) |
| precision_recall_fscore_support(y_true, y_pred) |
| precision_score(y_true, y_pred[, labels, …]) |
| recall_score(y_true, y_pred[, labels, …]) |
| zero_one_loss(y_true, y_pred[, normalize, …]) |
一些是通常用于分級的:
| ? |
|---|
| dcg_score(y_true, y_score[, k]) |
| ndcg_score(y_true, y_score[, k]) |
而且許多是用于二分類和多標簽問題的,但不適用于多分類:
| ? |
|---|
| average_precision_score(y_true, y_score[, …]) |
| roc_auc_score(y_true, y_score[, average, …]) |
下面的章節中,我們會描述每一個函數。
從二分類到多分類多標簽
??一些度量基本上是針對二進制分類任務(例如f1_score,roc_auc_score)定義的。在這些情況下,假設默認情況下,正類標記為1(盡管可以通過pos_label參數進行配置),默認情況下僅評估正標簽。?
??將二進制度量擴展為多類或多標簽問題時,數據將被視為二分類問題的集合,即一對多類型。下面是綜合二分類度量的值的多種方法,不同的方法可能適用于不同的情況,通過參數average來選擇:
"macro"簡單地計算二分類度量的平均值,賦予每個類別相同的權重。"weighted"計算的是每個二分類度量的加權平均。"micro",每個二分類對總體度量的貢獻是相等的(除了作為樣本權重的結果)。"sample"僅適用于多標簽問題。它不計算每個類別的度量,而是計算評估數據中每個樣本的真實和預測類別的度量,并返回(sample_weight-weighted)平均值。- 選擇
average = None將返回每個類的分值。
這里不懂的可以看下面章節——多分類多標簽分類的例子?
??多標簽數據用于指標評估時,也像二分類的標簽傳入一個類別標簽的數組,傳入的是一個標簽矩陣,元素ij在樣本i的標簽是j的時候取值為1,否則為0。
精確度
??accuracy_score函數用于計算預測的精度。在多標簽分類中,函數返回子集精度。 如果樣本的整套預測標簽與真正的標簽組一致,則子集精度為1.0; 否則為0.0。如果y^iy^i是第i個樣本的預測值,yiyi是相應的真實值,則nsamplesnsamples上的精度為:?
accuracy(y,y^)=1nsamples∑nsamples?1i=01(y^i=yi)accuracy(y,y^)=1nsamples∑i=0nsamples?11(y^i=yi)
import numpy as np
from sklearn.metrics import accuracy_score
y_pred = [0, 2, 1, 3] y_true = [0, 1, 2, 3] accuracy_score(y_true, y_pred) # 用比值的方式輸出精度 輸出:0.5 accuracy_score(y_true, y_pred, normalize=False) # 用計數的方式輸出精度 輸出:2?
'''多標簽的情況'''
accuracy_score(np.array([[0, 1], [1, 1]]), np.ones((2, 2))) # 輸出 0.5?
解釋一下多標簽的情況,先看樣本0——第一行,它的真實標簽是[0, 1],預測標簽為[1, 1],預測錯誤。樣本1——第二行,它的真實標簽是[1, 1],預測標簽是[1, 1],預測正確。所以最后的預測精度為0.5。如果將參數
normalize設為False的話,將輸出1,即表示預測正確了一個。
Cohen’s kappa
??函數cohen_kappa_score()計算Cohen’s kappa統計量。這個方法是想比較不同的人表計的正確率,而非針對分類器。kappa分數是-1和1之間的數字。0.8以上的分數通常被認為是不錯的結果; 零或更低表示沒有效果(就像瞎蒙的一樣)。?
??Kappa分數可用于二分類問題或多分類問題,但不能用于多重標簽問題。
from sklearn.metrics import cohen_kappa_score
y_true = [2, 0, 2, 2, 0, 1] y_pred = [0, 0, 2, 2, 0, 2] cohen_kappa_score(y_true, y_pred) # 輸出0.4285...?
混亂矩陣
??confusion_matrix()函數通過計算混亂矩陣來評估分類精度。根據定義,元素ij表示:真實值為i,預測值為j的情況的個數,例子如下:
from sklearn.metrics import confusion_matrix
y_true = [2, 0, 2, 2, 0, 1] y_pred = [0, 0, 2, 2, 0, 2] confusion_matrix(y_true, y_pred)?
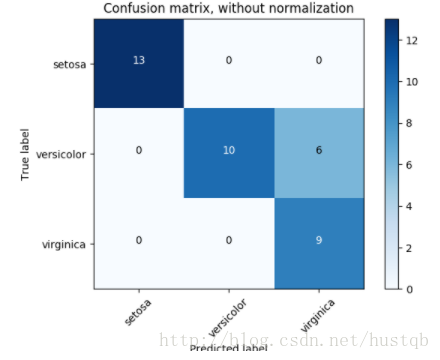
解釋一下,對于元素(0, 0)的值為2,表示真實值為0,預測為0的次數為2次;元素(2,0)的值為1, 表示真實值為2, 預測為0的次數為1次。矩陣的所有元素和為2+1+1+2 = 6,表示一共有6個樣本參與預測。下圖是一個關于混亂矩陣的例子:?
y_true = [0, 0, 0, 1, 1, 1, 1, 1] y_pred = [0, 1, 0, 1, 0, 1, 0, 1] '''t表示正例,f表示反例,n表示預測錯誤,p表示預測正確''' tn, fp, fn, tp = confusion_matrix(y_true, y_pred).ravel() tn, fp, fn, tp # 輸出 (2, 1, 2, 3)?
分類報告
??函數classification_report()創建了一個展示主要分類度量指標的文本報告,這是一個使用自定義target_name和內部標簽的小例程。
from sklearn.metrics import classification_report
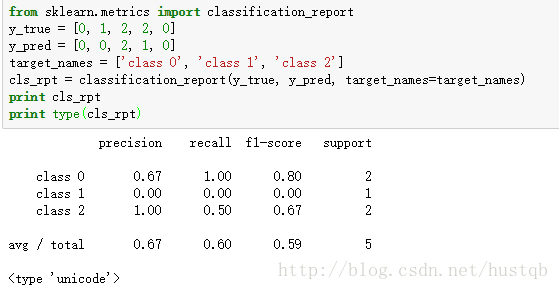
y_true = [0, 1, 2, 2, 0] y_pred = [0, 0, 2, 1, 0] target_names = ['class 0', 'class 1', 'class 2'] cls_rpt = classification_report(y_true, y_pred, target_names=target_names) print cls_rpt print type(cls_rpt)?
可以看到,函數
classification_report()的運行結果是一個字符串,形如一個列表:列名是各種評分方法,行名是自定義的標簽名字。
漢明損失
??函數hamming_loss()計算兩組樣本之間的平均漢明損失或漢明距離。如果y^jy^j是給定樣本的第j個標簽的預測值,則yjyj是相應的真實值,而nlabelsnlabels是類或標簽的數量,則兩個樣本之間的漢明損失LhammingLhamming定義為:?
LHamming(y,y^)=1nlabels∑nlabels?1j=01(y^j≠yj)LHamming(y,y^)=1nlabels∑j=0nlabels?11(y^j≠yj)
是不是感覺很熟悉,哈哈,回憶一下之前的
accuracy_score()。但是,漢明損失前面分式的分母是標簽個數而不像精確度一樣是樣本個數,所以它們在多標簽問題的結果不一樣。漢明損失頗像下面的Jaccard相關系數。
from sklearn.metrics import hamming_loss
y_pred = [1, 2, 3, 4]
y_true = [2, 2, 3, 4] hamming_loss(y_true, y_pred) # 二分類單一標簽 輸出 0.25- 1
- 2
- 3
- 4
hamming_loss(np.array([[0, 1], [1, 1]]), np.zeros((2, 2))) # 二分類多標簽 輸出:0.75- 1
Jaccard 相似性相關系數
??jaccard_similarity_score()函數計算標簽集對之間的平均(默認)或Jaccard相似系數的總和,也稱為Jaccard索引。設真實標簽集yiyi和預測標簽集合y^iy^i,將第i個樣本的Jaccard相似系數定義為?
J(yi,y^i)=|yi∩y^i||yi∪y^i|J(yi,y^i)=|yi∩y^i||yi∪y^i|。?
在二分類和多分類中,Jaccard相似系數分數等于分類的精度。
真實標簽集與預測標簽集的交集就是預測正確的部分;對于并集來說,一般情況下,預測機的結果都不會超綱,這種情況下并集就是真實標簽集。然而在負載情況下,預測機的結果可能超出了真實標簽集。?
確實跟二分類或多分類的accuracy_score()很相似。但是對于多標簽問題,它們是截然不同的結果。
import numpy as np
from sklearn.metrics import jaccard_similarity_score
y_pred = [0, 2, 1, 3] y_true = [0, 1, 2, 3] jaccard_similarity_score(y_true, y_pred) # 輸出 0.5?
jaccard_similarity_score(y_true, y_pred, normalize=False) # 輸出 0.75- 1
到這里,都是大家常見的幾種評分方式,也比較好理解,諸君可能覺得有點無聊,那么下面就是重頭戲了。
準確率、召回率和F度量
??直觀地說,準確率(presicion)是分類器不錯判的能力,并且召回率(recall)是分類器找到正例的能力。
F-measure()(FβFβ和F1F1測量)可以解釋為presicion和recall的加權調和平均值,?FβFβ最大是1,最小是0。當ββ?= 1時,FβFβ和F1F1是等效的,并且此時回調和精度權值相等。precision_recall_curve()通過改變判定閾值來計算關于真實值的presicion-recall曲線和分類器分值。average_precision_score()函數根據預測分數計算出平均精度(AP)。該分數對應于presicion-recall曲線下的面積。該值在0和1之間,而且更高更好。?
下面是幾個計算準確率、召回率和F度量的函數:
| function | comment |
|---|---|
| average_precision_score(y_true, y_score[, …] | 計算平均準確度(AP) |
| f1_score(y_true, y_pred[, labels, …]) | 計算F1分數 |
| fbeta_score(y_true, y_pred, beta[, labels, …]) | 計算F-beta分數 |
| precision_recall_curve(y_true, probas_pred) | 計算precision-recall曲線 |
| precision_recall_fscore_support(y_true, y_pred) | 計算準確率、召回率、F度量和類別數 |
| precision_score(y_true, y_pred[, labels, …]) | 計算準確度 |
| recall_score(y_true, y_pred[, labels, …]) | 計算召回率 |
PS:precision_recall_curve()函數僅限于二分類;average_precision_score()函數僅限于二分類和多標簽。
二分類
??在二進制分類任務中,術語positive和negative是指分類器的預測情況,術語true和false是指該預測是否對應于外部判斷 有時被稱為’觀察”)。 給出這些定義,我們可以制定下表:
| ? | 真實類別 (observation) | |
| 預測類別(expectation) | tp (true positive) 預測為positive,預測正確 | fp (false positive) 預測為positive,預測錯誤 |
| fn (false negative)預測為negetive,預測錯誤 | tn (true negative)預測為negetive,預測正確 | |
定義準確率、召回率和F度量:?
precision=tptp+fpprecision=tptp+fp,?
recall=tptp+fnrecall=tptp+fn,?
Fβ=(1+β2)precision×recallβ2precision+recallFβ=(1+β2)precision×recallβ2precision+recall.?
例程:
from sklearn import metrics
y_pred = [0, 1, 0, 0] y_true = [0, 1, 0, 1] print metrics.precision_score(y_true, y_pred) # 準確率 輸出:1.0 print metrics.recall_score(y_true, y_pred) # 召回率 輸出: 0.5 print metrics.f1_score(y_true, y_pred) # f1分數 輸出:0.66 print metrics.fbeta_score(y_true, y_pred, beta=0.5) # f-beta 輸出: 0.83 print metrics.fbeta_score(y_true, y_pred, beta=1) # 輸出: 0.66,與f1分數相等 print metrics.fbeta_score(y_true, y_pred, beta=2) # 輸出: 0.55 print metrics.precision_recall_fscore_support(y_true, y_pred, beta=0.5) # 最后輸出數組(array([ 0.66..., 1. ]), array([ 1. , 0.5]), array([ 0.71..., 0.83...]), array([2, 2]...))?
最后一個,函數
metrics.precision_recall_fscore_support()的輸出比較復雜,其實它是輸出了很多結果。首先樣本數據一共有2中標簽:0和1,所以輸出是成對的,分別對應著兩種類別。然后4組數據分別表示:準確率、召回率、f度量和支持的類別數。
import numpy as np
from sklearn.metrics import precision_recall_curve
from sklearn.metrics import average_precision_score y_true = np.array([0, 0, 1, 1]) y_scores = np.array([0.1, 0.4, 0.35, 0.8]) precision, recall, threshold = precision_recall_curve(y_true, y_scores) '''可以看到準確率和召回率是負相關的''' print precision # 輸出: array([ 0.66..., 0.5 , 1. , 1. ]) print recall # 輸出: array([ 1. , 0.5, 0.5, 0. ]) print threshold # 輸出: array([ 0.35, 0.4 , 0.8 ]) print average_precision_score(y_true, y_scores) # 輸出: 0.83...?
多分類多標簽
??在多類和多標簽分類任務中,準確率、召回率和F度量的概念可以獨立地應用于每個類別。 如上所述,有幾種cross標簽的方法:特別是由average參數指定為average_precision_score(僅限多標簽),f1_score,fbeta_score,precision_recall_fscore_support,precision_score和recall_score函數。?
聲明一波記號:
- y表示預測值
- y^y^表示預測結果正確與否
- L表示標簽集
- S表示樣本集
- ysys表示樣本子集
- ylyl表示標簽子集
- y^sy^s和y^ly^l同理
- P(A,B):=|A∩B||A|P(A,B):=|A∩B||A|
- R(A,B):=|A∩B||B|R(A,B):=|A∩B||B|
- Fβ(A,B):=(1+β2)P(A,B)×R(A,B)β2P(A,B)+R(A,B)Fβ(A,B):=(1+β2)P(A,B)×R(A,B)β2P(A,B)+R(A,B)?
然后,一些度量指標定義為:?
from sklearn import metrics
y_true = [0, 1, 2, 0, 1, 2] y_pred = [0, 2, 1, 0, 0, 1] print metrics.precision_score(y_true, y_pred, average='macro') # 輸出:0.22 print metrics.recall_score(y_true, y_pred, average='micro') # 輸出:0.33 print metrics.f1_score(y_true, y_pred, average='weighted') # 輸出:0.26 print metrics.fbeta_score(y_true, y_pred, average='macro', beta=0.5) # 輸出:0.23 print metrics.precision_recall_fscore_support(y_true, y_pred, beta=0.5, average=None) #輸出:數組如下 # (array([ 0.66..., 0. , 0. ]), array([ 1., 0., 0.]), array([ 0.71..., 0. , 0. ]), array([2, 2, 2]...))?
解釋一下:對于標簽0, 1, 2,它們的準確率分別是2323,?0202和0101。所以
macro的計算方式是13?(23+02+01)13?(23+02+01);micro的計算方式是2+0+03+2+12+0+03+2+1,即分子相加除以分母相加。
print metrics.recall_score(y_true, y_pred, labels=[1, 2], average='micro') # 輸出:0.0 print metrics.precision_score(y_true, y_pred, labels=[0, 1, 2, 3], average='macro') # 輸出:0.166..- 1
- 2
上面代碼顯示了
label參數的作用。
Hinge損失
??hinge_loss()函數使用hinge損失計算模型和數據之間的平均距離,這是僅考慮預測誤差的單側度量。 (Hinge損失用于最大化邊緣分類器,如SVM支持向量機)如果標簽用+1和-1編碼,則y是真實值,w是由decision_function()輸出的預測值,則hinge損失定義為:?
LHinge(y,w)=max{1?wy,0}=|1?wy|+LHinge(y,w)=max{1?wy,0}=|1?wy|+?
如果有兩個以上的標簽,則由于Crammer&Singer,hinge_loss()使用了多類型變體。?
如果ywyw是真實標簽的預測值,并且ytyt是所有其他標簽的預測值的最大值,其中通過決策函數輸出預測值,則多類hing損失由以下定義:?
LHinge(yw,yt)=max{1+yt?yw,0}LHinge(yw,yt)=max{1+yt?yw,0}?
這里有一個小例子演示了在二分類問題中使用svm分類器和hinge_loss函數:
from sklearn import svm
from sklearn.metrics import hinge_loss
X = [[0], [1]]
y = [-1, 1]
est = svm.LinearSVC(random_state=0)
est.fit(X, y) # 訓練好線性分類器
pred_decision = est.decision_function([[-2], [3], [0.5]]) print pred_decision # 輸出預測值:array([-2.18..., 2.36..., 0.09...]) print hinge_loss([-1, 1, 1], pred_decision) # 輸出:0.3...?
下面的例子演示了多分類問題中,使用svm分類器和hinge_loss函數:
X = np.array([[0], [1], [2], [3]])
Y = np.array([0, 1, 2, 3]) labels = np.array([0, 1, 2, 3]) est = svm.LinearSVC() est.fit(X, Y) pred_decision = est.decision_function([[-1], [2], [3]]) y_true = [0, 2, 3] hinge_loss(y_true, pred_decision, labels) # 輸出:0.56...?
Log損失
??log損失也稱logistic回歸損失或交叉熵損失,是一個建立在概率上的定義。它通常用于(多項式)邏輯回歸和神經網絡,以及期望最大化的一些變體中。?
log損失是一個負值:?
Llog(y,p)=?logPr(y|p)=?(ylog(p)+(1?y)log(1?p))Llog(y,p)=?log?Pr?(y|p)=?(ylog?(p)+(1?y)log?(1?p))?
這可以擴展到如下多種情形:?
Llog(Y,P)=logPr(Y|P)=?1N∑N?1i=0∑K?1k=0yi,klogpi,kLlog(Y,P)=log?Pr?(Y|P)=?1N∑i=0N?1∑k=0K?1yi,klog?pi,k
from sklearn.metrics import log_loss
y_true = [0, 0, 1, 1]
y_pred = [[.9, .1], [.8, .2], [.3, .7], [.01, .99]] log_loss(y_true, y_pred) # 輸出:0.1738...?
注意,這里的預測值是概率。比如y_pred[0]為[0.9, 0.1]表示,預測為0的概率是0.9,預測為1的概率是0.1。?
下面將0.1738是怎么計算出來的。首先應該知道,在log損失中,y的值只有0和1,其概率的和是1。?
還是對于第一個樣本y_pred[0],其log損失為?(0×log(0.9)+1×log(0.9))?(0×log(0.9)+1×log(0.9)),然后求剩余的1、2、3樣本并取平均值可得log損失。
Matthews 相關系數
??matthews_corrcoef函數計算二進制類的Matthews相關系數(MCC)。引用維基百科:
“The Matthews correlation coefficient is used in machine learning as a measure of the quality of binary (two-class) classifications. It takes into account true and false positives and negatives and is generally regarded as a balanced measure which can be used even if the classes are of very different sizes. The MCC is in essence a correlation coefficient value between -1 and +1. A coefficient of +1 represents a perfect prediction, 0 an average random prediction and -1 an inverse prediction. The statistic is also known as the phi coefficient.”
大意:
Matthews相關系數(MCC)用于機器學習,作為二分類質量的量度。它考慮到正例反例、判斷對判斷錯,通常被認為是可以使用的平衡措施,即使類別大小極其不同。 MCC本質上是-1和+1之間的相關系數值。系數+1表示完美預測,0表示平均隨機預測,-1表示反向預測。統計學也稱為phi系數。
在二分類的情況下,tp,tn,fp和fn分別是真正例,真反例,假正例和假反例數,MCC定義為?
MCC=tp×tn?fp×fn(tp+fp)(tp+fn)(tn+fp)(tn+fn)√MCC=tp×tn?fp×fn(tp+fp)(tp+fn)(tn+fp)(tn+fn).?
在多類案例中,馬修斯相關系數可以用K類的混淆矩陣C來定義。為了簡化定義,考慮以下中間變量:
- tk=∑KiCiktk=∑iKCik真正發生類k的次數,
- pk=∑KiCkipk=∑iKCkik類被預測的次數,
- c=∑KkCkkc=∑kKCkk正確預測的樣本總數,
- s=∑Ki∑KjCijs=∑iK∑jKCij樣本總數。
然后將多類MCC定義為:?
MCC=c×s?∑Kkpk×tk(s2?∑Kkp2k)×(s2?∑Kkt2k)√MCC=c×s?∑kKpk×tk(s2?∑kKpk2)×(s2?∑kKtk2)?
當有兩個以上的標簽時,MCC的值將不再在-1和+1之間。相反,根據真實標簽的數量和分布,最小值將在-1和0之間,最大值始終為+1。?
這是一個小例子,說明matthews_corrcoef()函數的用法:
from sklearn.metrics import matthews_corrcoef
y_true = [+1, +1, +1, -1] y_pred = [+1, -1, +1, +1] matthews_corrcoef(y_true, y_pred) # 輸出:-0.33?
總之,Matthews相關系數也是一個根據真實值和預測值對預測模型進行評分的一個方法
ROC
??函數roc_curve()計算 receiver operating characteristic curve或者說是ROC曲線。 引用維基百科:
“A receiver operating characteristic (ROC), or simply ROC curve, is a graphical plot which illustrates the performance of a binary classifier system as its discrimination threshold is varied. It is created by plotting the fraction of true positives out of the positives (TPR = true positive rate) vs. the fraction of false positives out of the negatives (FPR = false positive rate), at various threshold settings. TPR is also known as sensitivity, and FPR is one minus the specificity or true negative rate.”
大意:
ROC或者是ROC曲線,是一個圖形圖,說明了二分類系統在鑒別閾值變化的情形下的性能。它通過在不同閾值設置下,TPR(正例中判對的概率)與FPR(被錯判為正例的概率)。TPR又稱為敏感度,FPR是1減去反例判對的概率。
該函數需要正確的二分類值和目標分數,這可以是正類的概率估計,置信度值或二分類判決。 這是一個如何使用roc_curve()函數的小例子:
import numpy as np
from sklearn.metrics import roc_curve
y = np.array([1, 1, 2, 2]) scores = np.array([0.1, 0.4, 0.35, 0.8]) fpr, tpr, thresholds = roc_curve(y, scores, pos_label=2) print fpr # 輸出:[ 0. 0.5 0.5 1. ] print tpr # 輸出:[ 0.5 0.5 1. 1. ] print thresholds # 輸出:[ 0.8 0.4 0.35 0.1 ]?
thresholds閾值的意義:所有的樣本都要和這個閾值比較,如果大于這個閾值就是正例。所以,這個閾值越大,反例被錯判為正例的可能性越小,當然,很多比較小的正例也會被忽略從而導致TPR也較小。
下圖是一個ROC曲線的例子:?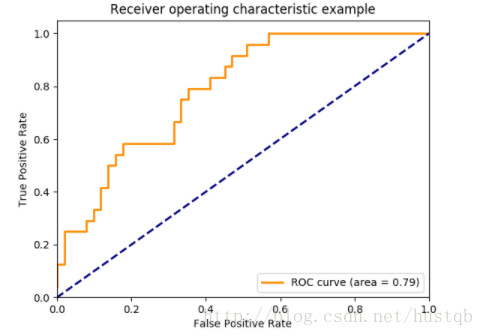
roc_auc_score()函數計算ROC曲線下面積,也由AUC或AUROC表示。 通過計算roc曲線下的面積,曲線信息總結為一個數字。
import numpy as np
from sklearn.metrics import roc_auc_score
y_true = np.array([0, 0, 1, 1]) y_scores = np.array([0.1, 0.4, 0.35, 0.8]) roc_auc_score(y_true, y_scores) # 輸出:0.75?
在多標簽分類中,roc_auc_score()函數通過如上所述的標簽平均來擴展。?
與諸如子集精確度,漢明損失或F1度量相比,ROC不需要優化每個標簽的閾值。 如果預測的輸出已被二進制化,則roc_auc_score()函數也可用于多類分類。
0-1損失
??zero_one_loss()函數通過nsamplesnsamples計算0-1分類損失(L0?1)(L0?1)的和或平均值。 默認情況下,函數對樣本進行標準化。 要獲得L0?1L0?1的總和,將其normalize參數置為False。?
??在多標簽分類中,如果所有預測標簽與真實標簽嚴格匹配,則zero_one_loss()為1,如果存在任何錯誤,則為0。 默認情況下,函數返回對子集不完全預測的百分比, 如果想讓函數返回個數,設置normalize參數為False如果y^iy^i是第i個樣本的預測值,yiyi是相應的真實值,則0-1損失L0?1L0?1定義為:?
L0?1(yi,y^i)=1(y^i≠yi)L0?1(yi,y^i)=1(y^i≠yi)
from sklearn.metrics import zero_one_loss
y_pred = [1, 2, 3, 4] y_true = [2, 2, 3, 4] print zero_one_loss(y_true, y_pred) # 輸出:0.25 表示預測錯誤的百分比是0.25 print zero_one_loss(y_true, y_pred, normalize=False) # 輸出:1 表示有1個預測錯誤?
print zero_one_loss(np.array([[0, 1], [1, 1]]), np.ones((2, 2))) # 輸出:0.5 print zero_one_loss(np.array([[0, 1], [1, 1]]), np.ones((2, 2)), normalize=False) # 輸出1- 1
- 2
似乎跟前面的
accuracy_score()有點像(我覺得是一樣的)。
Brier score損失
??brier_score_loss()函數計算二分類的Brier分數。引用維基百科:
The Brier score is a proper score function that measures the accuracy of probabilistic predictions. It is applicable to tasks in which predictions must assign probabilities to a set of mutually exclusive discrete outcomes.
Brier分數在用于衡量預測的準確性方面,是一個合適的評分函數。它適用于預測必須將概率分配給一組相互排斥的離散結果的任務。
??該函數返回實際結果與可能結果的預測概率之間的均方差的得分。實際結果必須為1或0(真或假),而實際結果的預測概率可以是0到1之間的值。Brier損失也在0到1之間,分數越低(均方差越小),預測越準確。它可以被認為是對一組概率預測的“校準”的度量。?
BS=1N∑Nt=1(ft?ot)2BS=1N∑t=1N(ft?ot)2?
其中:N是預測的總數,ftft是實際結果otot的預測概率。?
這是一個使用這個函數的小例子:
from sklearn.metrics import brier_score_loss
y_true = np.array([0, 1, 1, 0]) y_true_categorical = np.array(["spam", "ham", "ham", "spam"]) y_prob = np.array([0.1, 0.9, 0.8, 0.4]) y_pred = np.array([0, 1, 1, 0]) print brier_score_loss(y_true, y_prob) # 輸出;0.055 print brier_score_loss(y_true, 1-y_prob, pos_label=0) # 輸出;0.055 print brier_score_loss(y_true_categorical, y_prob, pos_label="ham") # 輸出;0.055 print brier_score_loss(y_true, y_prob > 0.5) # 輸出;0可以看到與之前不同的地方:真實標簽y_true輸入的不管是字符串還是數字都沒有規定正例or反例,而是通過
brier_score_loss()函數的pos_lable參數決定的。
多標簽分級度量
??在多標簽學習中,每個樣本可以具有與之相關的任何數量的真實標簽,最后靠近真實標簽的獲得更高的分值和等級。
Coverage誤差
??coverage_error()函數計算包含在最終預測中的標簽的平均數,以便預測所有真正的標簽。如果您想知道有多少頂級評分標簽,您必須平均預測,而不會丟失任何真正的標簽,這很有用。因此,此指標的最好的情況(也就是最小值)是正確標簽的平均數量。?
注意:我們的實現的分數比Tsoumakas等人在2010年提供的分數大1。這樣就可以包含一種特例:實例的正確標簽為0。?
??給定一個二進制的真實標簽矩陣,y?∈{0,1}nsamples×nlabels∈{0,1}nsamples×nlabels?,和相應的分值f^∈Rnsamples×nlabelsf^∈Rnsamples×nlabels,coverage被定義為:?
coverage(y,f^)=1nsamples∑nsamples?1i=0maxj:yij=1rankijcoverage(y,f^)=1nsamples∑i=0nsamples?1maxj:yij=1rankij?
其中,rankij=∣∣{k:f^ik≥f^ij}∣∣rankij=|{k:f^ik≥f^ij}|。?
這是一個使用這個功能的小例子:
import numpy as np
from sklearn.metrics import coverage_error
y_true = np.array([[1, 0, 0], [0, 0, 1]])
y_score = np.array([[0.75, 0.5, 1], [1, 0.2, 0.1]])
coverage_error(y_true, y_score) # 輸出:2.5?
首先:這是一個用于多標簽的誤差計算函數。其次,具體怎么算的筆者也不太清楚,歡迎大家在回復里指教,最后這個誤差的意義我是知道的:?
上面例子的y_score實際上是一個rank(可以想成排名,積分)列表,只要真實標簽中的1對應的y_score中的值(也就是它的rank)是最大的,則誤差最小,最小為nlabel=1nsamplesnlabel=1nsamples。反之,當真是標簽中的1對應的y_score中的值是最小的,則誤差最大,最大為nlabel=1nlabel=1。
分級標簽平均準確度
??label_ranking_average_precision_score()函數實現標簽rank的平均精度(LRAP)。該度量值與average_precision_score()函數相關,但是基于標簽rank的信息,而不是準確率和召回率。?
??標簽rank的平均精度(LRAP)是分配給每個樣本的,rank一般較高真實標簽對rank一般較低的總標簽的比率的平均值。如果能夠為每個樣本相關標簽提供更好的rank,這個指標就會產生更好的分數。獲得的分數總是嚴格大于0,最佳值為1。如果每個樣本只有一個相關標簽,則標簽排名平均精度等于mean reciprocal rank。?
??給定一個二進制標簽矩陣,即y∈Rnsamples×nlabelsy∈Rnsamples×nlabels,以及它的對應的預測rankf^∈Rnsamples×nlabelsf^∈Rnsamples×nlabels,則平均精度定義為?
LRAP(y,f^)=1nsamples∑nsamples?1i=01|yi|∑j:yij=1|Lij|rankijLRAP(y,f^)=1nsamples∑i=0nsamples?11|yi|∑j:yij=1|Lij|rankij?
其中Lij={k:yik=1,f^ik≥f^ij}Lij={k:yik=1,f^ik≥f^ij},rankij=∣∣{k:f^ik≥f^ij}∣∣rankij=|{k:f^ik≥f^ij}|?
這是一個使用這個功能的小例子:
import numpy as np
from sklearn.metrics import label_ranking_average_precision_score
y_true = np.array([[1, 0, 0], [0, 0, 1]])
y_score = np.array([[0.75, 0.5, 1], [1, 0.2, 0.1]])
label_ranking_average_precision_score(y_true, y_score) # 輸出:0.416...?
這個的公式只能說比上一個
coverage_error()函數的方法更復雜,但是它們是同根同源的,解決的是同一個問題。只要知道這個函數的最大值是1,最小值大于0就行了。
分級損失
??label_ranking_loss()函數計算在樣本上的排序錯誤(即正例的rank低于反例)的標簽的rank損失的平均值(由正例和反例的倒數加權),最小值為0。?
??給定一個二進制標簽矩陣y∈{0,1}nsamples×nlabelsy∈{0,1}nsamples×nlabels,相應的預測rank為f^∈Rnsamples×nlabelsf^∈Rnsamples×nlabels,排名損失定義為:?
ranking\_loss(y,f^)=1nsamples∑nsamples?1i=01|yi|(nlabels?|yi|)∣∣{(k,l):f^ik<f^il,yik=1,yil=0}∣∣ranking\_loss(y,f^)=1nsamples∑i=0nsamples?11|yi|(nlabels?|yi|)|{(k,l):f^ik<f^il,yik=1,yil=0}|。?
這是一個使用這個功能的小例子:
import numpy as np
from sklearn.metrics import label_ranking_loss
y_true = np.array([[1, 0, 0], [0, 0, 1]])
y_score = np.array([[0.75, 0.5, 1], [1, 0.2, 0.1]])
label_ranking_loss(y_true, y_score) # 輸出:0.75?
y_score = np.array([[1.0, 0.1, 0.2], [0.1, 0.2, 0.9]]) # 這樣就能輸出最小loss
label_ranking_loss(y_true, y_score) # 輸出:0.0?
再次,公式不懂,但是
label_ranking_loss()還是與上面兩種都是同一問題解決方法的不同表達。
回歸度量
??sklearn.metrics模塊實現了幾個損失,評分和工具函數來衡量回歸表現。其中一些已被增強以處理多輸出情形:mean_squared_error(),mean_absolute_error(),explain_variance_score()和r2_score()。?
??這些函數具有一個multioutput關鍵字參數,用于指定平均每個目標的分數或損失的方式。默認值為'uniform_average',它指定輸出均勻加權均值。如果傳遞形如(n_outputs,)的數組,則將其解釋為權重,并返回相應的加權平均值。如果指定了多重輸出為'raw_values',則所有未更改的單個分數或損失將以形狀數組(n_outputs,)返回。?
??r2_score()和interpret_variance_score()為multioutput參數接受一個附加值'variance_weighted'。該選項通過相應目標變量的方差導出每個單獨得分的加權。此設置量化了全局捕獲的未縮放的方差。如果目標變量的scale范圍不同,則該分數更好地解釋較高的方差變量。對于向后兼容性,multioutput ='variance_weighted'是r2_score()的默認值。將來會更改為uniform_average。
Explained variance score
??explain_variance_score()計算explained variance regression score.。?
如果y^y^是估計的目標輸出,則y為相應的(正確)目標輸出,Var為方差,標準偏差的平方,則說明的方差估計如下:?
explained_variance(y,y^)=1?Var{y?y^}Var{y}explained_variance(y,y^)=1?Var{y?y^}Var{y}?
最好的分數是1.0,值越低越差。?
以下是explain_variance_score()函數的一個小例子:
from sklearn.metrics import explained_variance_score
y_true = [3, -0.5, 2, 7] y_pred = [2.5, 0.0, 2, 8] explained_variance_score(y_true, y_pred) # 輸出:0.957.。。?
y_true = [[0.5, 1], [-1, 1], [7, -6]]
y_pred = [[0, 2], [-1, 2], [8, -5]]
print explained_variance_score(y_true, y_pred, multioutput='raw_values') # 輸出:[ 0.967..., 1. ] print explained_variance_score(y_true, y_pred, multioutput=[0.3, 0.7]) # 輸出:0.990...?
兩個方差的比值?解釋方差?這個分值有什么用?
均值絕對誤差
??mean_absolute_error()函數計算平均絕對誤差,對應于絕對誤差損失或l1范數損失的預期值的風險度量。如果y^iy^i是第i個樣本的預測值,yiyi是相應的真實值,則在nsamplesnsamples上估計的平均絕對誤差(MAE)被定義為?
MAE(y,y^)=1nsamples∑nsamples?1i=0|yi?y^i|.MAE(y,y^)=1nsamples∑i=0nsamples?1|yi?y^i|.?
這是一個使用mean_absolute_error()函數的小例子:
from sklearn.metrics import mean_absolute_error
y_true = [3, -0.5, 2, 7]
y_pred = [2.5, 0.0, 2, 8] mean_absolute_error(y_true, y_pred) # 輸出:0.5 y_true = [[0.5, 1], [-1, 1], [7, -6]] y_pred = [[0, 2], [-1, 2], [8, -5]] mean_absolute_error(y_true, y_pred) # 輸出:0.75?
print mean_absolute_error(y_true, y_pred, multioutput='raw_values') # 輸出:【0.5, 1】
print mean_absolute_error(y_true, y_pred, multioutput=[0.3, 0.7]) # 輸出:0.849...?
均值平方誤差
??mean_squared_error()函數計算均方誤差,與平方(二次)誤差或損失的預期值對應的風險度量。如果y^iy^i是第i個樣本的預測值,yiyi是相應的真實值,則在nsamplesnsamples上估計的均方誤差(MSE)被定義為?
MSE(y,y^)=1nsamples∑nsamples?1i=0(yi?y^i)2.MSE(y,y^)=1nsamples∑i=0nsamples?1(yi?y^i)2.?
這是一個使用mean_squared_error()函數的小例子:
from sklearn.metrics import mean_squared_error
y_true = [3, -0.5, 2, 7]
y_pred = [2.5, 0.0, 2, 8] print mean_squared_error(y_true, y_pred) # 輸出:0.375 y_true = [[0.5, 1], [-1, 1], [7, -6]] y_pred = [[0, 2], [-1, 2], [8, -5]] print mean_squared_error(y_true, y_pred) # 輸出:0.7083?
均值平方對數誤差
??mean_squared_log_error()函數計算對應于平方對數(二次)誤差或損失的預期值的風險度量。如果y^iy^i是第i個樣本的預測值,yiyi是相應的真實值,則在nsamplesnsamples上估計的均方對數誤差(MSLE)被定義為?
MSLE(y,y^)=1nsamples∑nsamples?1i=0(loge(1+yi)?loge(1+y^i))2.MSLE(y,y^)=1nsamples∑i=0nsamples?1(loge?(1+yi)?loge?(1+y^i))2.。?
其中loge(x)loge?(x)表示x的自然對數。 當目標具有指數增長的目標時,最適合使用這一指標,例如人口數量,商品在一段時間內的平均銷售額等。
注意,該度量對低于真實值的預測更加敏感。
這是一個使用mean_squared_log_error函數的小例子:
from sklearn.metrics import mean_squared_log_error
y_true = [3, 5, 2.5, 7]
y_pred = [2.5, 5, 4, 8] print mean_squared_log_error(y_true, y_pred) # 輸出:0.039.。 y_true = [[0.5, 1], [1, 2], [7, 6]] y_pred = [[0.5, 2], [1, 2.5], [8, 8]] print mean_squared_log_error(y_true, y_pred) # 輸出:0.044?
中位數絕對誤差
??median_absolute_error()是非常有趣的,因為它可以減弱異常值的影響。 通過取目標和預測之間的所有絕對差值的中值來計算損失。如果y^iy^i是第i個樣本的預測值,yiyi是相應的真實值,則在nsamplesnsamples上估計的中值絕對誤差(MedAE)被定義為?
MedAE(y,y^)=median(∣y1?y^1∣,…,∣yn?y^n∣)MedAE(y,y^)=median(∣y1?y^1∣,…,∣yn?y^n∣)
median_absolute_error()不支持multioutput。
這是一個使用median_absolute_error()函數的小例子:
from sklearn.metrics import median_absolute_error
y_true = [3, -0.5, 2, 7] y_pred = [2.5, 0.0, 2, 8] median_absolute_error(y_true, y_pred) # 輸出:0.5?
R2R2?score,定義相關性
??r2_score()函數計算R^2,即確定系數,可以表示特征模型對特征樣本預測的好壞。 最佳分數為1.0,可以為負數(因為模型可能會更糟)。對于一個總是在預測y的期望值時不關注輸入特征的連續模型,它的R^2分值是0.0。如果y^iy^i是第i個樣本的預測值,yiyi是相應的真實值,則在nsamplesnsamples上估計的分數R^2被定義為?
R2(y,y^)=1?∑nsamples?1i=0(yi?y^i)2∑nsamples?1i=0(yi?yˉ)2R2(y,y^)=1?∑i=0nsamples?1(yi?y^i)2∑i=0nsamples?1(yi?yˉ)2?
其中yˉ=1nsamples∑nsamples?1i=0yiyˉ=1nsamples∑i=0nsamples?1yi?
這是使用r2_score()函數的一個小例子:
from sklearn.metrics import r2_score
y_true = [3, -0.5, 2, 7]
y_pred = [2.5, 0.0, 2, 8] print r2_score(y_true, y_pred) # 0.948... y_true = [[0.5, 1], [-1, 1], [7, -6]] y_pred = [[0, 2], [-1, 2], [8, -5]] print r2_score(y_true, y_pred, multioutput='variance_weighted') # 0.938... y_true = [[0.5, 1], [-1, 1], [7, -6]] y_pred = [[0, 2], [-1, 2], [8, -5]] print r2_score(y_true, y_pred, multioutput='uniform_average') # 0.936... print r2_score(y_true, y_pred, multioutput='raw_values') # [ 0.965..., 0.908...] print r2_score(y_true, y_pred, multioutput=[0.3, 0.7]) # 0.925...聚類度量
??sklearn.metrics模塊實現了多種損失函數、評分函數和工具函數。 有關更多信息,請參閱集聚類性能評估部分。
簡陋評分器
??在進行監督學習的過程中,簡單清晰的檢查包括將一個估計模型與簡單的經驗法則進行比較。?DummyClassifier實現了幾種簡單的分類策略:
stratified根據訓練數據類的分布產生隨機數據。most_frequent總是將結果預測為訓練集中最常用的標簽。prior總是預測為先前最大的那個類。uniform產生均勻隨機預測。constant總是預測為用戶提供的常量標簽。這種方法的主要靠的是F1分值,此時的正例數量較小。
為了說明DummyClassifier,首先讓我們創建一個不平衡的數據集:
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split iris = load_iris() X, y = iris.data, iris.target y[y != 1] = -1 X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)?
然后再來比較一下SVC和most_frequent:
from sklearn.dummy import DummyClassifier
from sklearn.svm import SVC
clf = SVC(kernel='linear', C=1).fit(X_train, y_train) print clf.score(X_test, y_test) # 0.63... clf = DummyClassifier(strategy='most_frequent',random_state=0) clf.fit(X_train, y_train) print clf.score(X_test, y_test) # 0.57...?
可以看出,
SVC的效果不比簡陋的分類器(dummy classifier)號多少,下面,讓我們換一下svc的核函數:
clf = SVC(kernel='rbf', C=1).fit(X_train, y_train)
clf.score(X_test, y_test) # 0.97...??我們看到準確率提高到近100%。建議使用交叉驗證策略,以便更好地估計精度。更一般地說,當分類器的準確度太接近隨機時,這可能意味著出現了一些問題:特征沒有幫助,超參數沒有正確調整,數據分布不平衡等?
DummyRegressor還實現了四個簡單的經驗法則:
mean:預測訓練目標的平均值。median:預測訓練目標的中位數。quantile:預測用戶提供的分數量的訓練目標。constant:預測用戶提供的常數值。
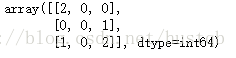





)



的使用)



)




)

