(Review cs231n) Backpropagation and Neural Network

損失由兩部分組成：

數據損失+正則化損失（data loss + regularization）

想得到損失函數關于權值矩陣W的梯度表達式，然后進性優化操作（損失相當于海拔，你在山上的位置相當于W，你進行移動，需要知道你到底是向下走了還是向上走了，所以可通過梯度或者是斜率來知道，你的目標是不斷的移動你的W就是位置，使你找到谷底就是損失最小的，但是有可能會存在你找到局部的谷底，就是所謂的局部最優)。

我們使用梯度下降算法，進行迭代運算，計算梯度進行權值的更新，一直循環執行這個操作，最后會停留在損失函數的低值點相當于在訓練數據集上的最好表現。

梯度下降

1. 數值梯度

寫起來容易但是運算太慢，使用微積分很快但是可能會有錯誤，所以我們需要進行梯度檢查，先通過運算得到解析梯度，然后使用數值梯度二次檢查他的準確性

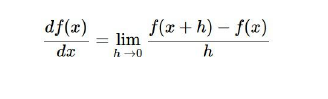
2. 計算圖（computational graph）

使用運算圖的形式表現出來顯得十分的龐大，below is the computational graph of SVM.

如果是卷積神經網路，這個計算圖會非常的龐大，所以想把計算圖(運算表達式)都寫下來并不實際，計算圖會不斷的重復運行，表達式不現實，時間的耗費，所以:

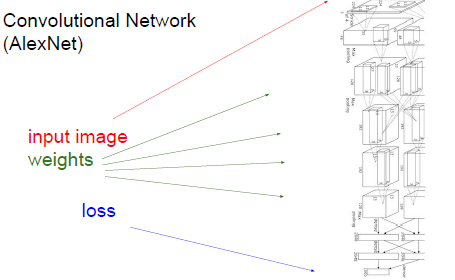
用一些函數將中間變量轉換成最終的損失值，結合輸入和梯度來得到最終的損失函數。

例子：f(x,y,z) =（x+y）z?

基于這些輸入得到表達式的梯度，引進中間變量q，表達式將變為一個加法式和一個乘法式，則轉變為了f=qz,分別求出f對x,y,z的偏導，在計算圖中我們對所有的中間變量都進行求偏導的計算，知道我們建立的表達式是使梯度基于輸入值的一個公式。

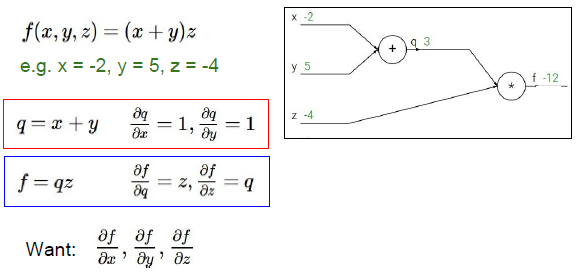
從右端開始作為遞歸運算的起點：

1. 先考慮f對f的偏導，為一個identity function 值為1, 所以這個恒等函數的梯度為1

2. 考慮f對z的偏導，是中間變量q，即x+y, 梯度為3，說明了z對最終結果是積極的影響，也就說給z一個小增量h，整個運算圖的輸出結果也會增加3h，

3. 考慮f對q的偏導，求得的結果是z，值為-4，如果給q一個小增量h,那么運算圖的輸出結果會減少4h，因為斜率是-4.

4. 計算y的梯度，求得的結果是-4，遵守鏈式法則，乘積運算，q中y的梯度和f中q的梯度相乘，這可以看作是反向傳播的體現。x和y的導數都為1，x、y對q都有正向的影響。斜率為1，對x加上增量h，q也會增加h，最終y影響到整個運算圖的輸出結果，所以你將y對q的影響和q對最終損失的影響相乘，進行遞歸在整個運算圖，增加y會使得運算圖的最終結果以4倍的速率減少，使最終結果減少。

整個計算圖非常的龐大，輸入集x、y和輸出集z，進行反向的遞推。

可以得到局部梯度，對她們進行只是加法或乘法，x和y對于輸出值的影響。

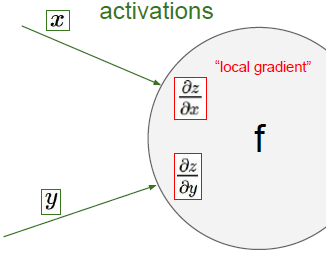
因此，我們只要得到最終的損失，就可以逆推回去，運算鏈路的最終輸出的影響到底有多大。要知道dl/dz這個梯度的流向是反向的的。

要得到結合輸入與梯度得到最終損失的關系，dL/dx=dL/dz*dz/dx，局部梯度與loss與輸出的梯度相乘，x對于該運算鏈路最終結果的影響如下圖所示，所以根據鏈式法則輸出結果的全局梯度乘以局部梯度，并且通過后者來改變他，y也一樣。? ?記住這些X和Y不是來自于同一個運算，所以你要將這一法則運用在整個的運算鏈路中，也因此這些參數對最終損失的影響都是相互的。她們會告知彼此，如果這是一個正的梯度，那么損失將會隨著他們增大而增大，如果是負梯度，那么損失將會隨著他增大而減小，并且他將鏈路中的所有局部梯度相乘，這個過程叫做反向傳播。

在運算鏈路中，這是一種通過鏈式法則來進行遞推的計算過程，這個鏈路中的每個中間變量，都會對最終的損失函數產生影響。

?補充知識，導數與斜率的關系（感謝美麗的閆小姐提供的公式推導?）

例子：

這個運算鏈路是一個二維的sigmoid函數，計算每一個輸入量對這一表達式的最終輸出的影響，這里計算他的梯度。

知道了每個小運算的局部梯度，我們在運算的時候可以直接使用他們（求導等于梯度），

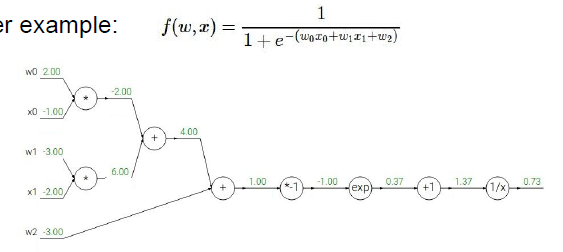
1. 從最后的梯度開始，寫上1，遞歸的開始，這是恒等函數的梯度

2. 1/x進行反向傳播，

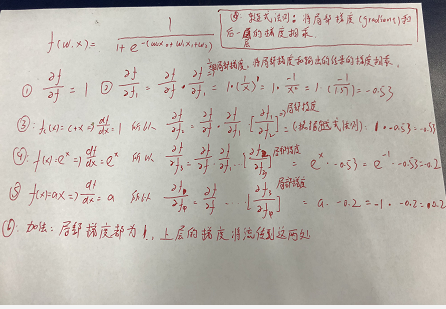
重要：

　　　1.根據鏈式法則，輸入到損失的梯度等于，局部梯度乘以后一層的梯度。

　　? ?2.經常遇到所有輸入的局部梯度都為1，不管后面的是多少，都將自身的梯度平均分發給他的輸入，根據鏈式法則，都乘以1，無影響。

　　? ?3.加法就像一個梯度分發器，如果從前面得到一個梯度，分發所有梯度。

　　? ?4. 反向計算時首先要得到所有的參數，比如所有的輸入和最終的損失函數，我們用正推法計算損失函數，然后再用反向傳播算法，對每一層運算計算（loss）對輸入的梯度，反向傳播算法就是多次不同的使用鏈式法則

　　? ?5. 反向傳播通常慢于正向傳播。

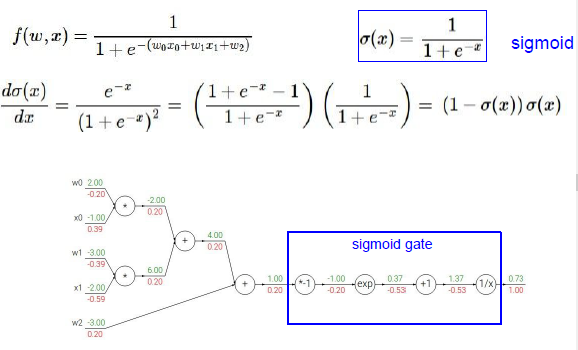
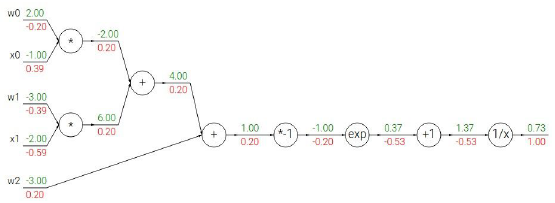
　　將sigmid的梯度表示為只有sigmoid函數的運算，那么就可以只進行一次sigmoid運算，然后只需要計算出sigmoid函數的局部梯度(1-sigmoid(x))sigmoid(x)就可以了(意思就是其實大的函數也可以直接視作一個整體計算梯度)，所以我們把它放在整個計算圖中。

　　一旦我們知道怎么計算局部梯度，通過鏈式法則和各部分之間乘法，其他一切都能求得，藍色框我們可以反向傳播通過S門，看起來輸入1，輸出是0.73，其實0.73就是sigmoid(x)值，通過之前sigmoid的梯度公式，得到sigmoid的局部梯度，正好這是在回路的盡頭，要乘以1.0 .

　　通常我們把整個表達式拆分開來，一次只計算一部分部分，或者把這部分看作是一個S門，這取決于我們打算把整個表達式拆分到何種程度(BP的拆分粒度)，所以局部梯度容易得到，我們整個看作一個S門。

　　當你看到一些運算部分要重復進行并且局部梯度很簡單，就可以組成一個合并單元。

　　通過計算圖，可以直觀的理解梯度是如何在整個神經網絡流動的，通過理解梯度的傳遞過程可以讓你了解一些問題，比如梯度消失的問題

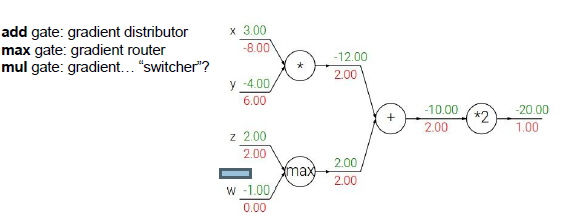
　　加法門：局部梯度為1，對兩個輸入的梯度都為2,梯度分配器，分配相等的梯度值。

　　最大值門：梯度路由，如果是一個簡單的二元表達式Max(x,y),這就是最大值運算門，求x,y上的梯度，那么你認為較大的輸入梯度為1（局部梯度），較小的對輸出沒有影響。反向傳播時，它會把梯度值分配給輸入值最大的線路，這就是梯度路由。

　　乘法門：梯度轉換器，

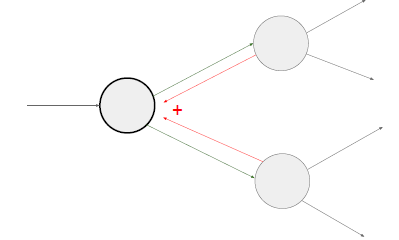
　　一個值通過分支被用于各部分的計算中，通過多元鏈式法則，正確的計算方法是把他們的結果相加，在反向傳播過程中，它們的梯度值也是相加的。

　　使用計算圖，構建神經網絡，在這些運算門的基礎上，我們需要確定整個圖的連接結構，哪些門相互連接，這些通常是在一個圖像或者網絡對象中說明的，這個對象有這兩部分，前向傳播和后向傳播，這是偽代碼：

思路：遍歷網絡中所有的運算門，并按正確的邏輯順序進行排列，意味著所有的輸入值在運算之前要知道這些標注信息，也就是從左到右的排列，要在各個門進行前向運算，并且由這個網絡對象確保各個部分按順序正確連接，

　　而反向傳播按照相反順序進行，反向傳播經過各個門，各個門之間的梯度相互傳遞，并計算出分解開的各梯度值，事實上網絡對象就是對這些門進行簡單的封裝，以后發現這些門會被稱作層，對各層結果的簡單封裝。

?運算門的實現，定義一個類：最終求得整個損失函數關于各個變量的梯度，L關于z的偏導就是我們要求的值，這由dz代表，這所有的變量都是標量，dz也是數字，表示輸入在回路最后的影響。

計算圖中各個門之間的梯度可以正確傳遞，反向傳播中，如果由支路合并，就要把所有梯度相加，所以在前向過程中，把這些大量的數據存儲下來，反向可能會用，如果在正向過程中存儲的了局部梯度值，那么就不需要記住其他中間值，需要利用各運算門及偏置值在反向運算之前記住所需值，

x1 class MultiplyGate(object):
 2     
 3      def forward(x,y):
 4             z = x*y
 5             self.x = x # 需要記住輸入值和其他出現過的中間微分值
 6             self.y = y
 7             return z
 8      def backward(dz)  # dz= dl/dz
 9             dx = self.y * dz # dl/dz * dz/dx
10             dy = self.x * dz # dl/dz * dz/dy
11             return [dx,dy]