參考：b站教學視頻FPGA：Cordic算法介紹與實現_嗶哩嗶哩_bilibili

? ? ? ?FPGA硬件實現加減法、移位等操作比較簡單，但是實現乘除以及函數計算復雜度高且占用資源多，常見的計算三角函數/平方根的求解方式有①查找表：先把函數對應結果存在存儲器中，根據輸入地址確定計算結果；②泰勒展開：把三角函數等函數求解展開成乘、除、加法進行求解。這兩種方法耗費ram/乘法器的資源巨大，為了僅用簡單的移位/加減法運算求解出復雜三角函數，提出了cordic算法。

????????cordic算法：coordinate rootation digital computer 坐標旋轉數字計算方法(硬件加速算法)。

類似于二分法，反復迭代，逐次逼近最終值，計算結果達到一定精度即可終止。與二分法不同的是，這里不是每次都改變二分之一的角度，而是改變二分之一的tan值，計算出對應角度，從而把復雜運算轉換為簡單的移位運算。

????????問題：已知某點坐標，①求旋轉到X軸需要的角度（向量模式）；②求旋轉某角度后的坐標（旋轉模式）； ???

對于旋轉模式：

模塊輸入為：坐標（x，y），要旋轉的角度z。輸出為：新的坐標(x1，y1)

根據新坐標的表達式，當輸入x=1/k，y=0時，輸出新的坐標為（cosz，sinz），即求出了cosz和sinz的值。

對于向量模式：

模塊輸入為：坐標（x，y），要旋轉的角度z。輸出為：新點的模長和角度。

根據輸出的表達式，當輸入為x=1，z=0時，輸出為(x,y)的角度：arctan(y/x)。

除此（圓周旋轉系統）之外，還有線性旋轉、雙曲旋轉兩種系統（迭代方程不同），根據需要查看文獻了解。

cordic算法用途之一：求相位角！

算法原理：

已知點（x1，y1），求旋轉角度z后的坐標（x2，y2）；

? ? ? ? ? ? ? ? ? ? ? ?

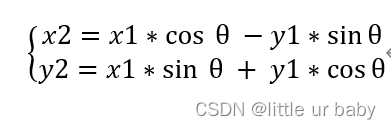
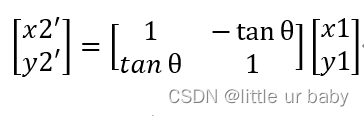
讓point1以θ1、θ2...... θn逐次逼近point2（此過程需調節正負號），直到誤差在可接受的范圍內：

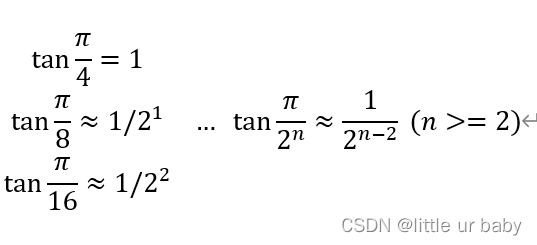
為了確保數值準確，即不取約等于，我們從函數值入手，只確保tan θn?=1/2n-2?，不去管θn的具體值，即存在

?求得如下角度：

后續的旋轉角度均按這個表格來旋轉：

?即把求解tanx函數轉化成了移位運算：

求解坐標就轉化成了加減運算和移位運算

對于系數cos，當角度趨近于0時，cos值趨近于1，可以知道當迭代次數足夠高時，伸縮因子基本是一個常數。按照上面角度的表格，通過計算可知，當迭代次數大于16次時，伸縮因子固定為0.6073，所以我們可以設置迭代次數高于16，把伸縮因子固定為0.673，在所有運算結束后再乘上去。

相位誤差取決了迭代的次數，用上述表格，當迭代次數確定為16次時，求解的相位誤差小于等于18°。

假定每次坐標旋轉θ，且tanθn=1/2n-2?，則可以得出單次迭代的坐標公式（沒考慮伸縮因子）：

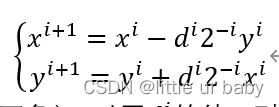
其中，di是旋轉方向的判定因子（正負）。對于di的值，引入角度累加器來判定，當累加的角度大于原始角度時，di為負，小于則di為正，

cordic算法即迭代算法（如以上迭代公式），通過多次迭代降低誤差，逼近目標值。

迭代有兩種模式：

①串行模塊：控制復雜，資源較少，速度較慢

②并行模塊：資源較多，速度較快，吞吐量大

atan函數：返回（-pi/2，pi/2）范圍的相位角；

atan2函數：返回（-pi，pi）范圍的相位角；

項目中用的是atan2函數。

quartus cordic ip核：

包含：

①sin cos

②atan2： 返回（-pi，pi）范圍的相位角；

③vector translate function：向量模式

④vector rotate function：旋轉模式

quartus 的cordic IP核用modelsim-se進行仿真時需要添加altera庫，暫時沒有進行仿真。（貌似如果用altera-modelsim就不需要再手動添加）

cordic算法的fpga實現：

?????? 求相位角：對于串行的方法來說，只需要根據迭代的表達式通過狀態機即可實現（線性序列機也可以，就是比較啰嗦，對于有相同迭代表達式的算法來說，狀態機方便）。