1.位圖

1.1概念

1. 引入
   給40億個不重復的無符號整數，沒排過序。給一個無符號整數，如何快速判斷一個數是否在這40億個數中。
   （1）遍歷： 時間復雜度O(N)
   （2）排序加二分：時間復雜度O(N*logN)
   其中 方法(2)是行不通的，因為內存很難裝下這么多數據(40億整數大概為16G)。
   方法(1)可行，但如果需要多次查詢很耗時。
   
   （3）位圖：數據是否在給定的整形數據中，結果是在或者不在，剛好是兩種狀態，那么可以使用一個二進制比特位來代表數據是否存在的信息，如果二進制比特位為1，代表存在，為0代表不存在。比如：
   
   方法（3）的優勢的建立起這個位圖后，查找任一數據在不在時間復雜度均為O(1)，而且只需要 16G / 32 = 0.5G(存儲整形需要16G，現在一個比特位就可代表，一個整形有32個比特位)，空間占用很小。
2. 概念
   所謂位圖，就是用比特位來存放某種狀態(哈希思想的體現)，適用于海量數據，數據無重復的場景。通常是用來判斷某個數據存不存在的。

1.2實現

namespace mystd
{//叫bitset只是單純和庫里面統一而已，接口命名也是//庫里面bitset使用基本也是這幾個接口template<size_t N>  //N表示要表示整數的范圍，即比特位個數class bitset  {public:bitset() {//初始化這里，可能存在浪費，但幾個比特位而已_bits.resize(N / 32 + 1, 0);}void set(size_t x)  //設置標記，表示x存在{//給你x，計算出x屬于第幾個整數，整數中的第幾個比特位int i = x / 32;  //第幾個int j = x % 32;  //第幾個比特位//把對應的_bits[i]的第[j]位修改為1即可，方法是將1左移j位，或運算即可_bits[i] |= (1 << j);}void reset(size_t x)  //去標記，表示x不存在{int i = x / 32;int j = x % 32;//把對應的_bits[i]的第[j]位修改為0即可，方法(1)是將1左移j位 (2)取反(j位置為0，其它位置為1) (3)進行與運算_bits[i] &= ~(1 << j);}bool test(size_t x)  //看x在不在{int i = x / 32;int j = x % 32;//取到_bits[i]的第j位即可return _bits[i] & (1 << j);  //非0即真，0即假}private:vector<int> _bits;};
}

1.3位圖應用

1. 快速查找某個數據是否在一個集合中
2. 排序 + 去重
3. 求兩個集合的交集、并集等

代碼：

#include<iostream>
#include<bitset>
using namespace std;
//位圖的應用
//快速查找某個數據是否在一個集合中
void test1()
{vector<int> a = { 0, 1, 2, 3, 4, 8, 99, 100, 150 };bitset<151> bit_set;for (auto e : a){bit_set.set(e);}int x = 0;while (cin >> x){if (bit_set.test(x)){cout << x << "存在" << endl;}else{cout << x << "不存在" << endl;}}
}//排序 + 去重
void test2()
{int a[] = {0, 1, 2, 3, 4, 8, 99, 99, 100, 100, 150};bitset<151> bit_set;vector<int> result;for (auto e : a){bit_set.set(e);}//實際中應該在建立位圖的過程中找出最大最小值，這里就不寫了//min = 0， max = 150;for (int i = 0; i <= 150; i++)   {if (bit_set.test(i)){result.push_back(i);}}for (auto e : result)  cout << e << " ";cout << endl;
}//求兩個集合的交集、并集等
void test3()
{int a1[] = { 0, 1, 2, 3 };int a2[] = { 0, 2, 2, 4, 5, 6 };//交集bitset<7> bit_set1;bitset<7> bit_set2;for (auto e : a1)  bit_set1.set(e);cout << "交集為：";for (auto e : a2){if (bit_set1.test(e) && bit_set2.test(e) == false){bit_set2.set(e);  //過濾掉多次出現的數據cout << e << " ";}}cout << endl;//并集cout << "并集為：";bitset<7> bit_set3;  //去掉a1中重復的部分for (auto e : a1){if (bit_set3.test(e) == false){cout << e << " ";bit_set3.set(e);}}for (auto e : a2){if (bit_set3.test(e) == false)  //把a2特有的提取出來{cout << e << " ";}}cout << endl;
}

2.布隆過濾器

2.1布隆過濾器的提出

想要判斷某個數據在不在：

1. 哈希表，空間消耗大。
2. 位圖，空間消耗小，只適用于整形。
3. 哈希位圖相結合，即布隆過濾器。可適用各種復雜數據，只要能通過哈希函數轉化出關鍵值即可。

2.2布隆過濾器的概念

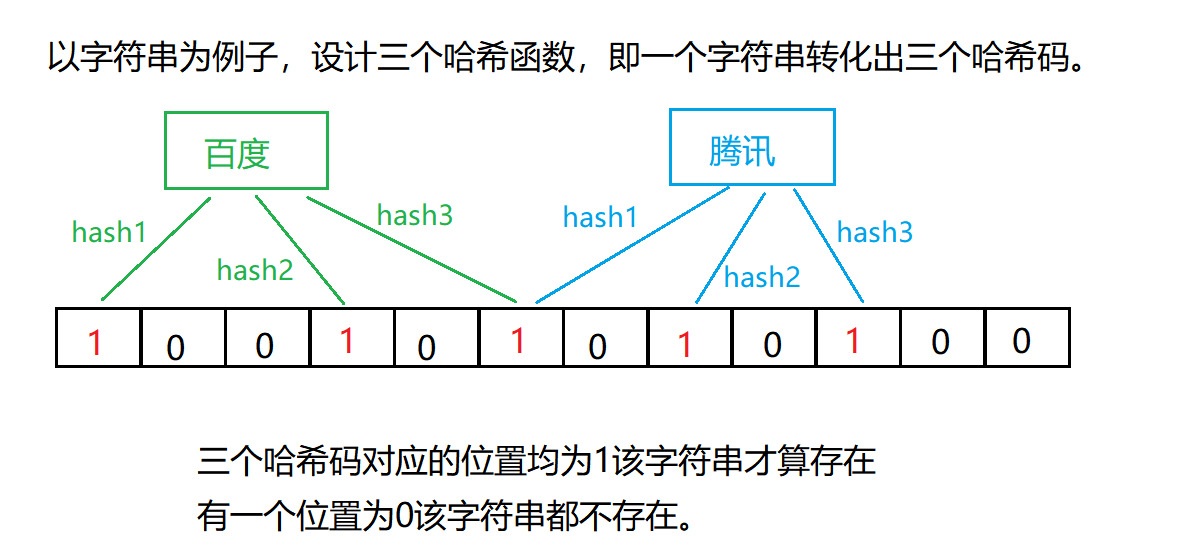
布隆過濾器是由布隆（Burton Howard Bloom）在1970年提出的 一種緊湊型的、比較巧妙的概率型數據結構，特點是高效地插入和查詢，可以用來告訴你 “某樣東西一定不存在或者可能存在”，它是用多個哈希函數，將一個數據映射到位圖結構中。此種方式不僅可以提升查詢效率，也可以節省大量的內存空間。

圖解：

2.3布隆過濾器的查找

結合前面可知，布隆過濾器的查找需要對多個位置進行判斷，都為1才認為存在，有一個為0認為不存在。

1. 布隆過濾器判斷存在，判斷不準確。
   
   
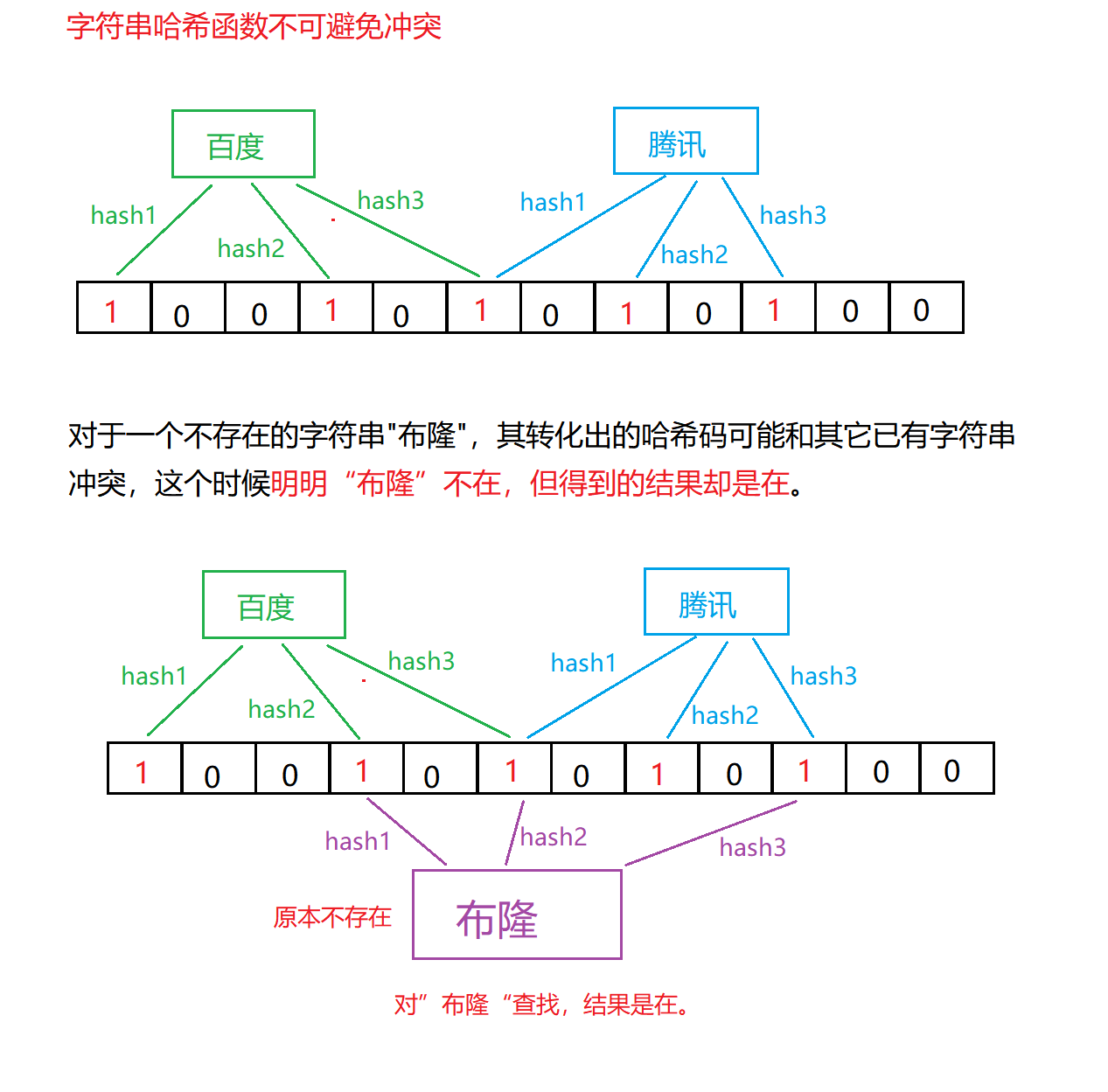
2. 布隆過濾器判斷不在，結果準確。

布隆過濾器存在誤判，為什么還要使用？

以用戶注冊為例，用戶名等信息存儲在服務器數據庫，每次注冊新用戶都要遍歷所有數據，消耗太大。這個時候可以考慮使用布隆過濾器，對于判斷不在的情況，是準確的，可以允許注冊；對于判斷在的情況就需要去遍歷數據。實際當中可以過濾掉大量的請求，提高效率。

2.4布隆過濾器的實現

//三個字符串哈希函數
struct BKDRHash
{size_t operator()(const string& key){// BKDRsize_t hash = 0;for (auto e : key){hash *= 31;hash += e;}return hash;}
};struct APHash
{size_t operator()(const string& key){size_t hash = 0;for (size_t i = 0; i < key.size(); i++){char ch = key[i];if ((i & 1) == 0){hash ^= ((hash << 7) ^ ch ^ (hash >> 3));}else{hash ^= (~((hash << 11) ^ ch ^ (hash >> 5)));}}return hash;}
};struct DJBHash
{size_t operator()(const string& key){size_t hash = 5381;for (auto ch : key){hash += (hash << 5) + ch;}return hash;}
};//布隆過濾器一般都是解決字符串
//關于布隆過濾器的長度，len = N * x，一般x取三以上，至于具體大小依據場景進行衡量
//（1）x過大，空間浪費
//（2）x過小，誤判較多（不在判斷為在），過濾效果不好
template<size_t N, size_t x = 5, class K = string, class HashFun1 = BKDRHash, class HashFun2 = APHash, class HashFun3 = DJBHash>
class BloomFilter
{void set(const K& key){//一次標記3個位置，要讓數值落在范圍內部size_t len = N * x;size_t hash1 = HashFun1()(key) % len;size_t hash2 = HashFun2()(key) % len;size_t hash3 = HashFun3()(key) % len;_bs.set(hash1);_bs.set(hash2);_bs.set(hash3);}bool test(const K& key){//看三個位置，有一個為0就返回falsesize_t len = N * x;size_t hash1 = HashFun1()(key) % len;if (_bs.test(hash1) == false)  return false;size_t hash2 = HashFun2()(key) % len;if (_bs.test(hash2) == false)  return false;size_t hash3 = HashFun3()(key) % len;if (_bs.test(hash3) == false)  return false;return true;}
private:bitset<N * x> _bs;
};

2.5布隆過濾器的刪除

布隆過濾器一般不能直接支持刪除工作，因為在刪除一個元素時，可能會影響其他元素。

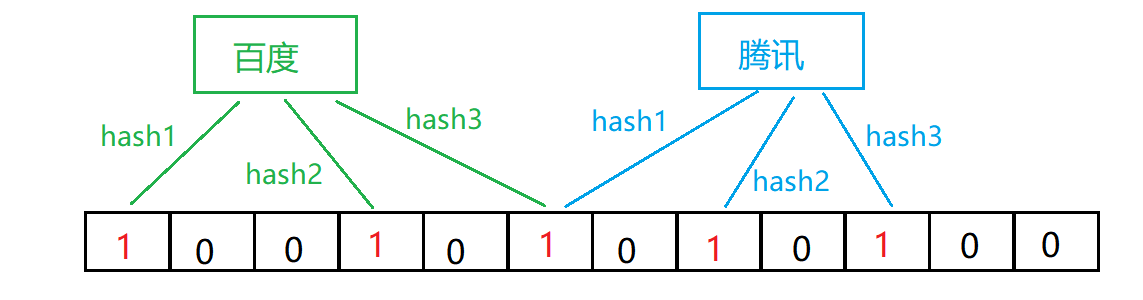
比如：刪除上圖中"騰訊"元素，如果直接將該元素所對應的二進制比特位置0，“百度”元素也被刪除了，因為這兩個元素在多個哈希函數計算出的比特位上剛好有重疊。

（了解）一定要支持刪除的話，可以采用引用計數的方法：
將布隆過濾器中的每個比特位擴展成一個小的計數器，插入元素時給k個計數器(k個哈希函數計算出的哈希地址)加一，刪除元素時，給k個計數器減一，通過多占用幾倍存儲空間的代價來增加刪除操作。

2.6布隆過濾器的優點

1. 增加和查詢元素的時間復雜度為:O(K), (K為哈希函數的個數，一般比較小)，與數據量大小無關
2. 哈希函數相互之間沒有關系，方便硬件并行運算
3. 布隆過濾器不需要存儲元素本身，在某些對保密要求比較嚴格的場合有很大優勢
4. 在能夠承受一定的誤判時，布隆過濾器比其他數據結構相比有很大的空間優勢
5. 數據量很大時，布隆過濾器可以表示全集，其他數據結構不能
6. 使用同一組散列函數的布隆過濾器可以進行交、并、差運算

2.7布隆過濾器的缺點

1. 有誤判率，即存在假陽性(False Position)，即判斷元素在集合中不準確(補救方法：再建立一個白名單，存儲可能會誤判的數據)
2. 不能獲取元素本身
3. 一般情況下不能從布隆過濾器中刪除元素
4. 如果采用計數方式刪除，可能會存在計數回繞（溢出了回滾到0）問題

3.海量數據面試題

3.1哈希切分

給一個超過100G大小的log file, log中存著IP地址, 設計算法找到出現次數最多的IP地址？

1. 100G過大，無法直接在內存中處理，可以先切割成100個小文件。先將IP轉化為整形key，然后key %= 100，相同IP會分到一樣的小文件。
2. 依此讀取這100個文件，找每個文件中出現次數最多，然后找出最大的那個。
3. 利用哈希切分可能存在沖突，如果某個小文件極大，可以更換哈希函數，對這個小文件再進行切分。

3.2位圖應用

1. 給定100億個整數，設計算法找到只出現一次的整數？
   解法一：整形范圍為40多億，位圖需要的空間為0.5G，存在出現多次的情況，即三種狀態，故一個比特位不夠，可以增加一位，即用兩個位圖實現。當結果為00時代表沒有出現、為01時代表出現了一次、為11時代表出現了多次。
   解法二：哈希切分，相同的數字一定會分到同個文件，對每個文件做統計即可。
2. 給兩個文件，分別有100億個整數，我們只有1G內存，如何找到兩個文件交集？
   （1）先哈希切分，key %= 500，文件一分出A0、A1、A2……A499，文件二分出B0、B1、B2……B499。其中相同的部分（交集）會被分到相同標號的文件，只需要A0對B0、A1對B1……A499對B499的兩兩找交集就行。
   （2）小文件過大的情況，更換哈希，再次切分即可。
3. 位圖應用變形：1個文件有100億個int，1G內存，設計算法找到出現次數不超過2次的所有整數
   （1）分析狀態：一、出現0次。二、出現1次。三、出現2次。四、出現2次以上。
   （2）有四種狀態，用兩個比特位即可表示，即使用兩個位圖。當結果為00、01、10時都屬于沒超過2次，當結果為11時代表結果超過了兩次。

3.3布隆過濾器

1. 給兩個文件，分別有100億個query，我們只有1G內存，如何找到兩個文件交集？分別給出精確算法和近似算法
   （1）近似算法，先讀取文件一，建立布隆過濾器。然后讀取文件二，依次判斷是否在布隆過濾器中，近似算法存在誤判。
   （2）精確算法，對兩個大文件進行哈希切分，兩兩小文件找交集即可。
2. 如何擴展BloomFilter使得它支持刪除元素的操作
   （1）數據量不大，可以用幾個位圖實現。
   （2）數據量大，一個哈希值對應的就不是一比特位了，而是一個整形。