Python中利用遺傳算法探索迷宮出路

更多資料獲取

📚 個人網站：ipengtao.com

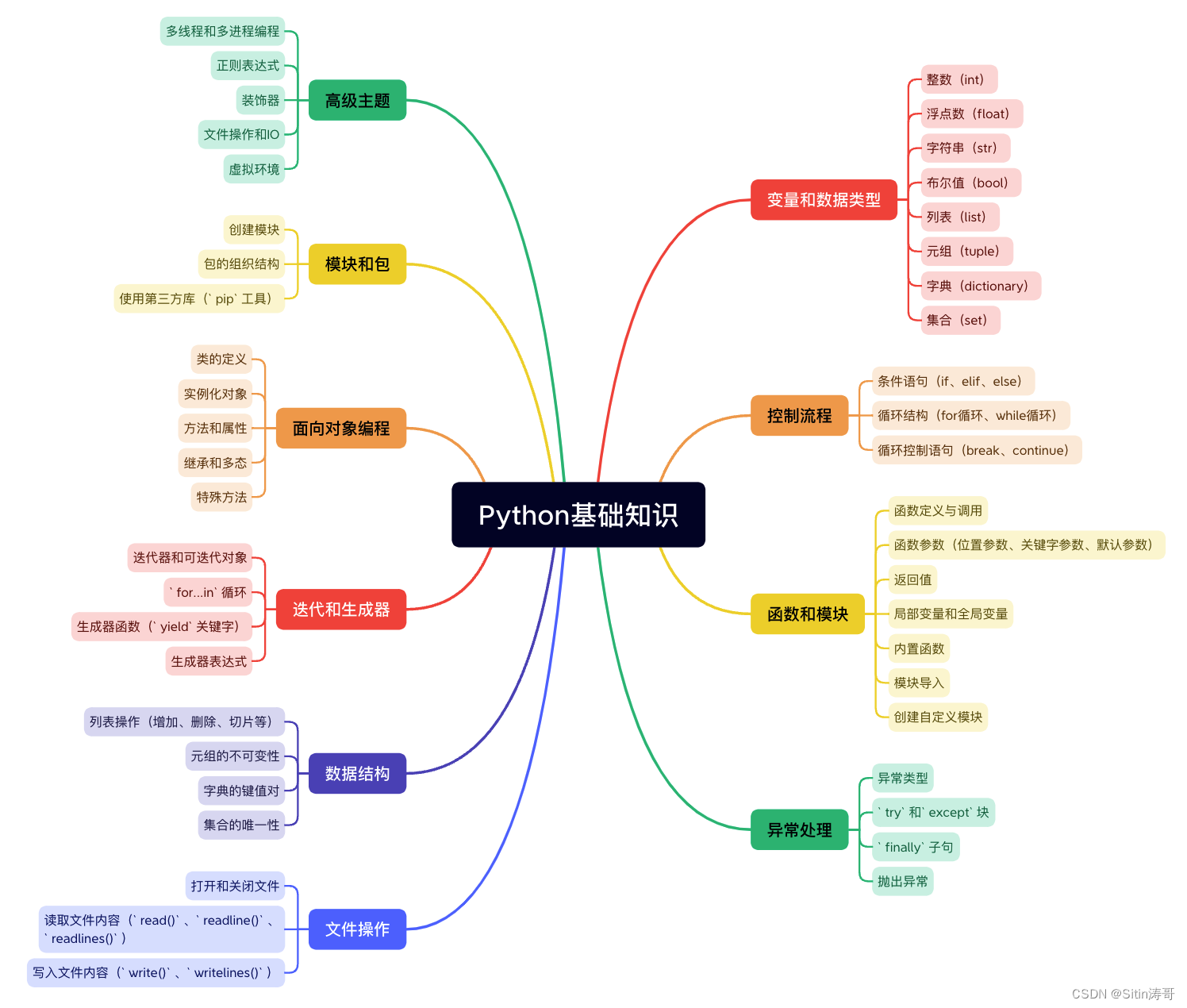
當處理迷宮問題時，遺傳算法提供了一種創新的解決方案。本文將深入探討如何運用Python和遺傳算法來解決迷宮問題。迷宮問題是一個經典的尋路問題，尋找從起點到終點的最佳路徑。遺傳算法是一種啟發式優化方法，適用于解決復雜問題，其中個體進化和自然選擇的概念被用于尋找最優解。

通過Python的代碼示例和解釋，將展示遺傳算法如何在迷宮問題中發揮作用。此外，本文還將解釋如何建模迷宮、編碼迷宮路徑、設計適應度函數以及實現遺傳算法的選擇、交叉和變異操作。

迷宮建模

當建模迷宮時，可以使用二維數組來表示不同的迷宮區域，如墻壁、路徑、起點和終點。以下是一個示例的Python代碼：

# 0 表示可通行的路徑
# 1 表示墻壁
# S 表示起點
# E 表示終點maze = [[1, 1, 1, 1, 1, 1, 1],[1, 0, 0, 0, 0, 0, 1],[1, 0, 1, 1, 1, 0, 1],[1, 0, 0, 0, 0, 0, 1],[1, 1, 1, 1, 1, 0, 1],[1, 'S', 0, 0, 0, 0, 1],[1, 1, 1, 1, 1, 1, 1]
]

上述代碼使用數字和字符表示不同類型的迷宮區域。其中，0表示可通行的路徑，1表示墻壁，'S’表示起點，'E’表示終點。這種表示方法使得迷宮的結構清晰，并便于編寫尋路算法。將迷宮抽象成二維數組，可以更輕松地進行路徑搜索和分析。

遺傳算法基礎

遺傳算法是一種基于生物進化過程的優化方法，通常用于解決搜索和優化問題。其基本原理涵蓋個體編碼、選擇、交叉和變異。

基本原理

個體編碼：在迷宮問題中，個體編碼可以表示為一串代表移動方向的序列。例如，使用字符串（比如"DDRRUULDL"）來代表向下、向右、向上、向左的移動。
選擇：在遺傳算法中，優秀的個體通常更有可能被選擇為下一代的父代。這涉及到通過一種適應度函數來評估每個個體的性能。
交叉：被選中的個體會以某種方式進行“交叉”，從而生成下一代個體。在迷宮問題中，交叉可以是路徑序列的交換和組合，以產生新的路徑。
變異：隨機性是遺傳算法的一個關鍵部分。在交叉后，一些新個體可能會經歷變異操作，以增加搜索空間。對于迷宮問題，變異可以是路徑序列中某些步驟的隨機變動。

解決迷宮問題

使用遺傳算法解決迷宮問題涉及將上述原理應用到迷宮的搜索過程中。基于迷宮的二維數組表示，個體編碼將是代表路徑的序列。適應度函數將評估路徑的有效性和質量，即路徑是否能成功走出迷宮。選擇、交叉和變異操作將在不斷迭代中產生出下一代更優秀的路徑，最終找到出路。

結合遺傳算法的基本原理和迷宮問題的特點，可以設計一個自定義的遺傳算法來解決迷宮問題，找到最優路徑以走出迷宮。

編碼個體

在遺傳算法中，編碼迷宮路徑可以采用字符串表示路徑的方向。例如，用單個字符串來表示移動的方向，其中每個字符代表一種移動方向。

在迷宮問題中，可以使用以下方式編碼迷宮路徑：

D：向下移動
U：向上移動
L：向左移動
R：向右移動

例如，一個路徑編碼可能如下所示：

path = "DDRURULDL"

上述編碼表示從起點到終點的一條路徑，其中每個字符代表了在迷宮中的一個移動方向。在迷宮問題中，將這樣的路徑編碼與遺傳算法相結合，通過選擇、交叉和變異操作，逐步尋找最佳路徑以走出迷宮。

適應度函數

適應度函數在遺傳算法中扮演著至關重要的角色。它用于評估每條路徑的優劣，并決定哪些路徑更有可能被選擇進入下一代。在迷宮問題中，適應度函數將評估路徑是否能夠成功通向迷宮出口。

下面是一個簡單的示例，演示如何編寫一個適應度函數來評估迷宮路徑的優劣：

def fitness_function(path, maze):# 獲取起點坐標start = find_starting_point(maze)x, y = start[0], start[1]# 按路徑移動for move in path:if move == 'D':x += 1elif move == 'U':x -= 1elif move == 'L':y -= 1elif move == 'R':y += 1# 檢查是否越界或撞墻if x < 0 or y < 0 or x >= len(maze) or y >= len(maze[0]) or maze[x][y] == 1:return 0  # 無效路徑，返回適應度為0# 到達終點if maze[x][y] == 'E':return 1  # 成功到達終點，返回適應度為1return 0  # 路徑未到達終點，返回適應度為0

適應度函數的基本思路是按照路徑移動，檢查路徑是否越界、撞墻或成功到達終點。如果路徑能夠成功通向迷宮的出口，適應度函數返回一個較高的值（如1），否則返回較低的值（如0）。通過這樣的適應度函數，可以評估路徑的有效性，并在遺傳算法中篩選出更優秀的路徑。

選擇、交叉和變異

在遺傳算法中，選擇、交叉和變異是重要的操作，用于產生新的路徑。這些操作基于已有的路徑，通過一定的機制生成下一代的路徑。

選擇（Selection）

選擇操作根據路徑的適應度函數對現有路徑進行篩選，挑選出更適應迷宮的路徑作為父代。一個簡單的選擇方法是基于路徑的適應度函數進行隨機選擇或按照適應度函數排序選擇。

def selection(population, maze):# 根據適應度函數對路徑進行排序或隨機選擇# 選擇較優秀的路徑作為父代# 返回父代路徑集合pass

交叉（Crossover）

交叉操作是將兩個父代路徑交叉產生新的子代路徑。在迷宮問題中，交叉可以是對兩個路徑的某個位置進行切割并交換部分路徑。

def crossover(parent1, parent2):# 對父代路徑進行交叉操作# 產生子代路徑# 返回子代路徑pass

變異（Mutation）

變異操作是為了增加種群的多樣性，對部分路徑進行隨機變動。在迷宮問題中，變異可以是路徑序列中某些步驟的隨機變動。

def mutation(path):# 對路徑進行變異操作# 產生新的路徑# 返回變異后的路徑pass

這些操作相互作用，通過選擇、交叉和變異不斷迭代，產生新的路徑，最終找到適應度更高的路徑，以解決迷宮問題。綜合使用這些操作可以提高尋找到最優路徑的可能性。

迷宮求解

在迷宮問題中，使用遺傳算法搜索最佳路徑是一個有趣而挑戰性的過程。通過綜合選擇、交叉和變異操作，可以編寫一個迷宮求解函數，該函數利用遺傳算法來尋找最佳路徑。

以下是一個示例，展示如何使用遺傳算法求解迷宮問題：

def solve_maze(maze, population_size, generations):population = generate_initial_population(population_size, maze)  # 生成初始種群for generation in range(generations):parents = selection(population, maze)  # 選擇父代new_population = []for i in range(0, len(parents), 2):parent1 = parents[i]parent2 = parents[i + 1] if i + 1 < len(parents) else parents[i]child = crossover(parent1, parent2)  # 交叉操作if random_chance_of_mutation():  # 變異操作child = mutation(child)new_population.append(child)population = new_population  # 更新種群# 找到最優路徑best_path = max(population, key=lambda path: fitness_function(path, maze))if fitness_function(best_path, maze) == 1:  # 如果找到最佳路徑return best_pathreturn None  # 未找到最佳路徑

這段代碼中的 solve_maze 函數使用遺傳算法來搜索最佳路徑。它包含了種群初始化、選擇、交叉、變異等操作，并循環進行多代迭代以尋找最優路徑。最終，它會返回找到的最佳路徑或 None（如果沒有找到解決方案）。

結果展示

展示最優路徑和在迷宮中標記路徑走向可以通過圖形化展示來呈現。這需要使用相應的可視化工具和技術。

下面是一個基本示例，演示如何展示最優路徑并在迷宮中標記路徑走向：

import matplotlib.pyplot as pltdef display_solution(maze, best_path):# 標記迷宮for i in range(len(maze)):for j in range(len(maze[0])):if maze[i][j] == 1:  # 墻壁plt.fill([j, j+1, j+1, j], [len(maze) - i, len(maze) - i, len(maze) - i + 1, len(maze) - i + 1], 'black')# 標記路徑x, y = find_starting_point(maze)for move in best_path:if move == 'D':x += 1elif move == 'U':x -= 1elif move == 'L':y -= 1elif move == 'R':y += 1plt.fill([y, y+1, y+1, y], [len(maze) - x, len(maze) - x, len(maze) - x + 1, len(maze) - x + 1], 'green')plt.show()

在這個示例中，使用了 matplotlib 庫來繪制迷宮和標記路徑。display_solution 函數接受迷宮和找到的最佳路徑作為參數，并在圖形中用不同的顏色標記出迷宮中的墻壁和最佳路徑。

總結

遺傳算法在解決迷宮問題中展現出了靈活性和適用性。通過編碼、選擇、交叉和變異等操作，遺傳算法能夠尋找到迷宮中的最佳路徑。遺傳算法利用了進化的思想，通過不斷迭代和進化，從初始種群中產生新的路徑，并篩選出更優秀的路徑。這種迭代過程使得算法能夠逐步優化路徑，找到迷宮的出口。其優勢在于可以處理多樣性、搜索空間大、應對復雜情況等。然而，也需要根據具體問題調整參數和方法以獲得更好的效果。

總體而言，遺傳算法作為一種搜索和優化的方法，在解決迷宮問題等特定領域具有廣泛的應用前景。通過本文的介紹，可以更好地理解遺傳算法，并將其應用于類似問題的求解中。