1、前言
什么是噪聲？
該像素與周圍像素的差別非常大，導致從視覺上就能看出該像素無法與周圍像素組成可識別的圖像信息，降低了整個圖像的質量。這種“格格不入”的像素就被稱為圖像的噪聲。如果圖像中的噪聲都是隨機的純黑像素或者純白像素，這樣的噪聲也被稱為“椒鹽噪聲”或“鹽噪聲”。

在圖像處理中，為了提升圖像的整體質量，通常我們需要對圖像進行模糊處理，即通過卷積運算對每個像素進行濾波或平滑，減少圖像的細節，使得圖像噪聲削弱，凸顯特征明顯的區域。圖像的卷積運算上一章已介紹，這里不再贅述。

2、均值濾波
把卷積核覆蓋在原圖上上依次滑過每個像素，計算卷積核覆蓋像素值的加權平均并賦值給被核中心覆蓋的那個像素值。比如下圖原圖像是一個5x5圖像，現在有個3x3卷積核，放在圖像最開始的位置，計算卷積核覆蓋的像素值的加權平均：
注意：均值濾波卷積核上的每個權重默認為1
卷積核：

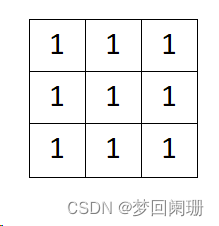
原圖像：

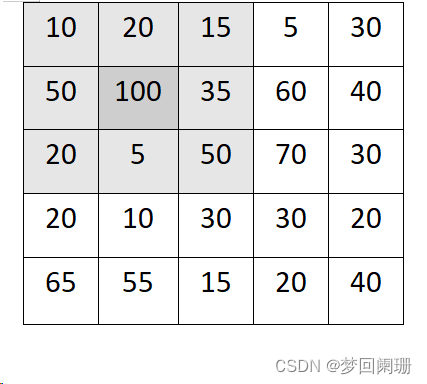
加權平均計算：

(10+20+15+50+100+35+20+5+50)* 1 / (1+1+1+1+1+1+1+1+1) = 33

核中心像素值，即原圖像第二行第二列會被重新賦值為33
下圖陰影區域為核中心滑過的區域：

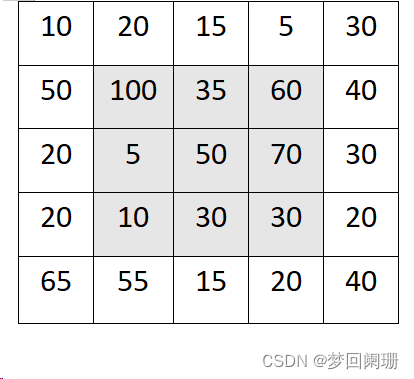
可以看到原圖像5x5，在經過卷積運算后圖像變為了3x3，如果想讓核中心掃過圖像邊緣像素，保持圖像大小不變，可以在原圖像基礎上拓展一層邊緣，如下圖：

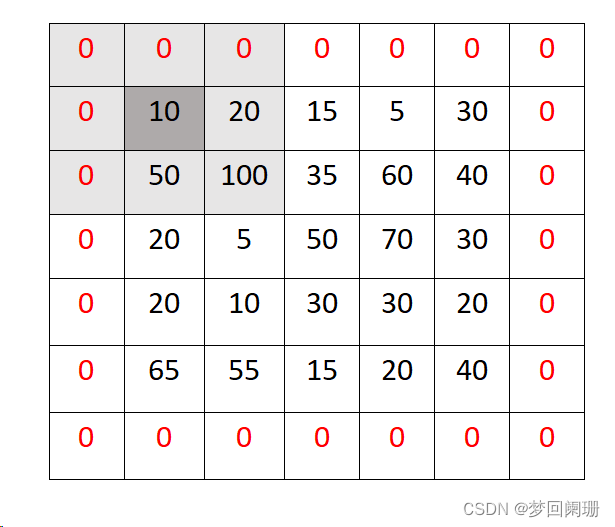
opencv提供了均值濾波接口如下：

void cv::blur(InputArray src, OutputArray dst, Size ksize, Point anchor=Point(-1,-1), int borderType=BORDER_DEFAULT)

src：原圖
dst：濾波后圖像
ksize：卷積核大小，注意卷積核只能是奇數，這樣才有核中心，建議使用3x3，5x5和7x7，卷積核越大圖像越模糊，卷積時間越長
anchor ：表示錨點(anchor)的位置，即被平滑的那個點。默認值Point(-1,-1)表示錨點位于核的中心。
borderType： 邊框模式用于推斷圖像外部的像素（一般默認）

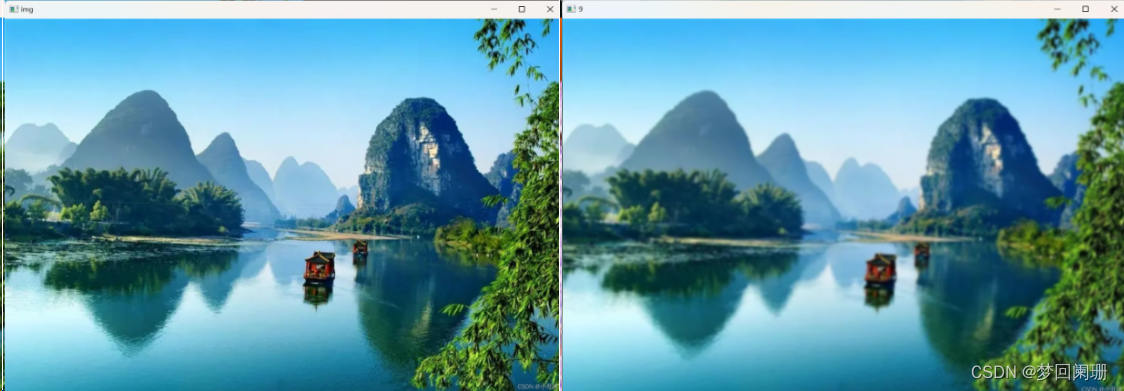
我們現在用5x5卷積核對下列圖像做均值濾波，可以看到右邊圖像已模糊處理：

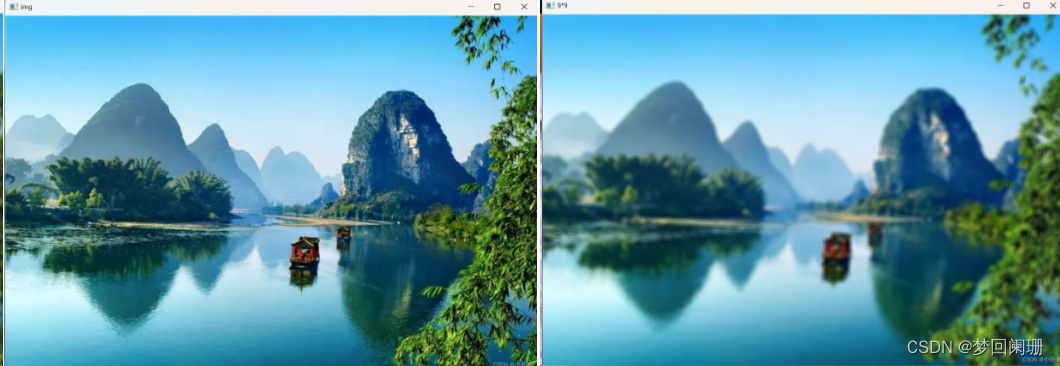
由于均值模糊是對窗口中所有像素點求平均值，在圖像的邊緣或者紋理豐富的地方也會變得模糊。為了盡可能的保留圖像中的邊緣信息，可以給不同位置的像素點賦以不同的權值。距離中心點越近的像素，權值越大，而遠離中心點的像素，權值也逐漸減少，這時候可以采用高斯濾波。

3、高斯濾波

在高斯濾波中卷積核的權重由高斯分布（正態分布）的取值來確定。
我們首先來介紹下高斯函數。

一維高斯函數：
從下圖中可以看到高斯分布（正態分布）是一種鐘形曲線，越接近中心，取值越大，越遠離中心，取值越小。我們給卷積核分配權重的時候，以曲線中心點為原點分配給核中心，核其他位置的權重按高斯曲線上遞減趨勢分配。
高斯函數中的參數σ表征著高斯濾波器寬度(決定著平滑程度)，當σ越大，高斯濾波器的頻帶就越寬，平滑程度就越高(越接近均值濾波)．通過調節平滑程度參數σ，可調整圖像的平滑程度。


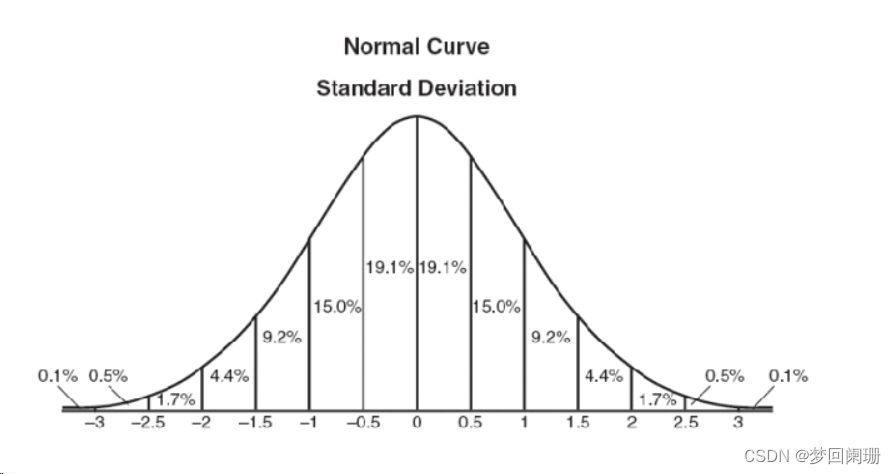
概率密度函數也為高斯函數。因為該函數只有一個變量x，所以我們也稱該函數為一維高斯函數。

再回到一維高斯函數圖中，圖中X軸的數值表示標準差的大小，比如0.5表示0.5個標準差大小，對應的高斯曲線上面的數值為0.5sigma，在0-0.5sigma區間內占比為19.1%。當我們取-3sigma-3sigma區間，占比達到99.8%，默認該段分布包含了所有情況。

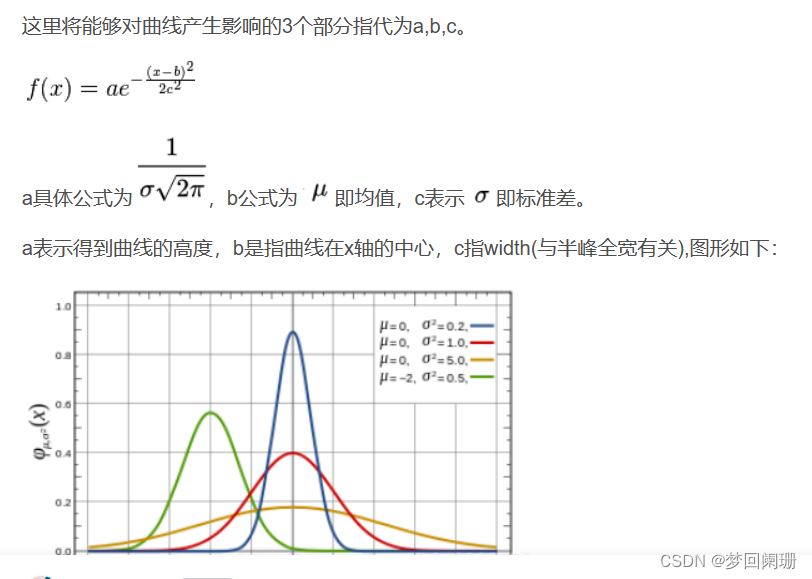
二維高斯函數：
因為圖像是二維空間，涉及XY兩個方向，這時候用一維高斯函數進行處理顯然不太合適，這時引入二維高斯函數是一個很好的解決方案。

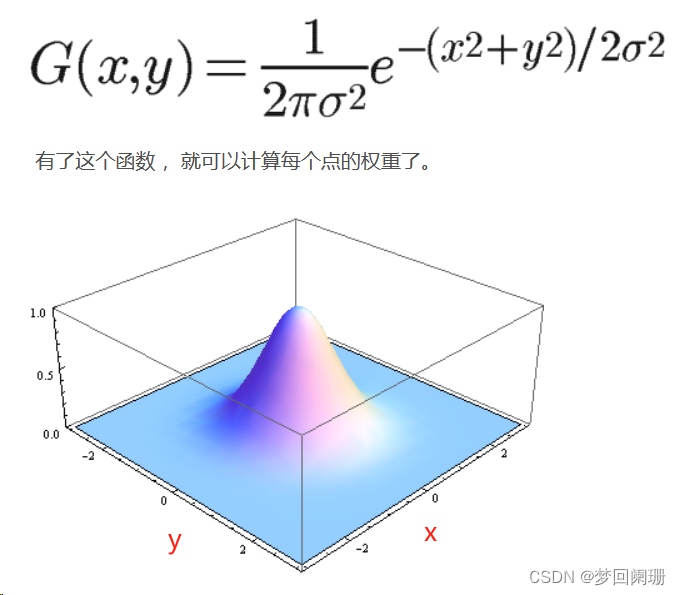
引入二維高斯函數進行模糊處理：

假設一個高斯函數的卷積和模板是5*5，那么他這25個點的x，y具體取值為：

此時只需要假定一個sigma值，即可確定一個高斯核，比如：

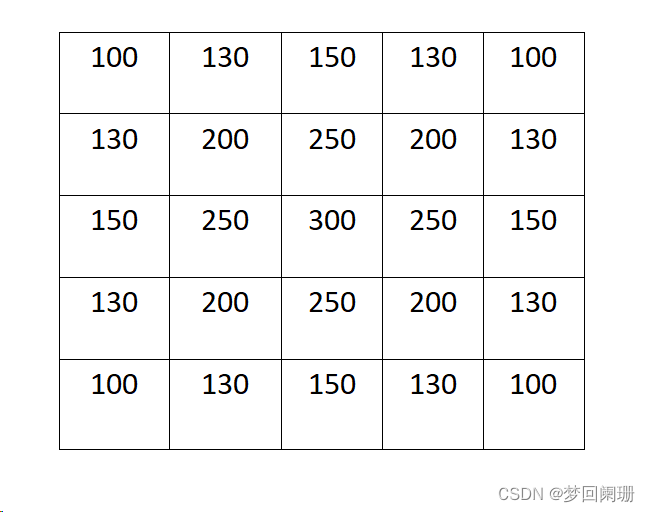
但是這個高斯核不完整，因為他求出的5*5的卷積核進行卷積操作時，改變了圖像原始的0-255的范圍。為解決該問題只需要將卷積核歸一化即可，即需要保證權重之和等于1，也就是卷積核中每一個值除以卷積的總和。

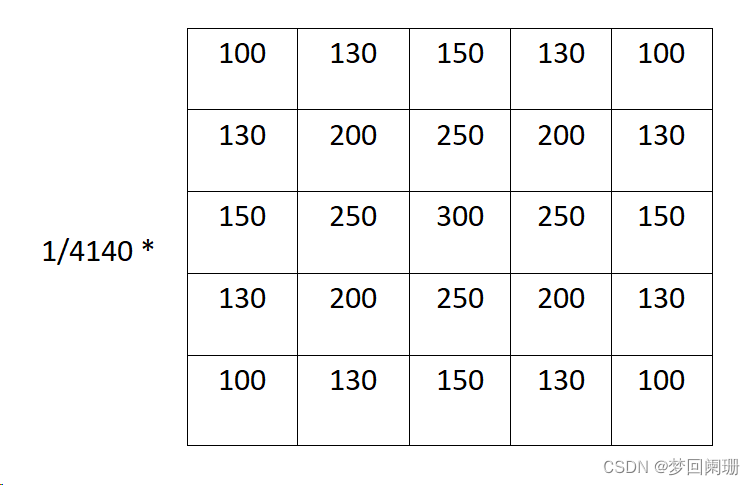
實際應用：
有個3x3高斯核，內部坐標如下：

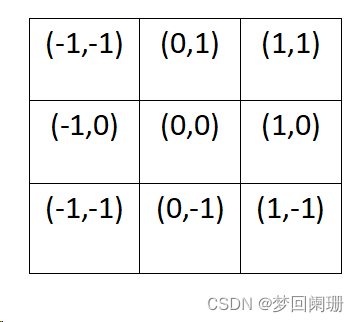
為了計算權重矩陣，需要設定標準差σ的值。假定σ=1.5，帶入二階高斯函數計算結果如下：

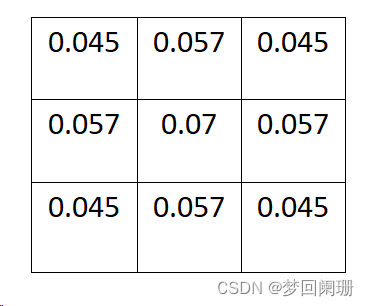
這9個點的權重總和等于0.479，如果只計算這9個點的加權平均，還必須讓它們的權重之和等于1，因此上面9個值還要分別除以0.479，得到最終的權重矩陣。

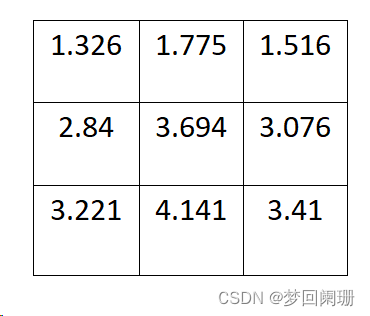
現在有了高斯核，可以進行圖像模糊計算，假設現有9個像素點，灰度值（0-255）如下：

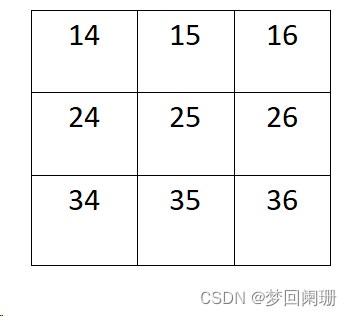
將高斯核覆蓋在圖像上，覆蓋的每個像素點乘以對應的權重再除以權重之和即可得到高斯核中心覆蓋的原圖像像素最新的值

(1.326*14 + 1.775*15 + 1.516*16 + 2.84*24 + 3.694*25 + 3.076*26 + 3.221*34 + 4.141*35 + 3.41*36) / 1 = 3.694

如果圖像很大，將高斯核依次在圖像上的每個像素點滑動，計算核中心的像素值，最后就得到了高斯模糊后的圖像。如果是彩色圖像可對RGB三通道分別進行高斯模糊計算。

opencv高斯模糊函數調用：

void GaussianBlur(
InputArray src,
OutputArray dst,
Size ksize,
double sigmaX,
double sigmaY = 0,
int borderType = BORDER_DEFAULT
);

src：原圖像
dst：高斯濾波后的圖像
ksize：濾波核的大小，寬、高必須是奇數，例如（3,3）、（5,5）等。
sigmaX：卷積核水平方向的標準差σ
sigmaY：卷積核垂直方向的標準差σ。修改 sigmaX 或 sigmaY 的值都可以改變卷積核中的權重比例。如果不知道如何設計這兩個參數值，就直接把這兩個參數的值寫成0，方法就會根據濾波核的大小自動計算出合適的權重比例。
boderType：可選參數，邊界樣式，建議使用默認值。
這里需要注意的是在二維高斯函數中標準差σ只有一種，沒有σ1和σ2，如果我們設置sigmaX等于sigmaY,這樣拿到的是一個圓形高斯核完全和二維高斯函數生成的一樣，如果sigmaX不等于sigmaY我們拿到的是一個橢圓形高斯核，即在X和Y方向調用了分別調用二維高斯函數計算高斯核，因為標準差σ不一樣。

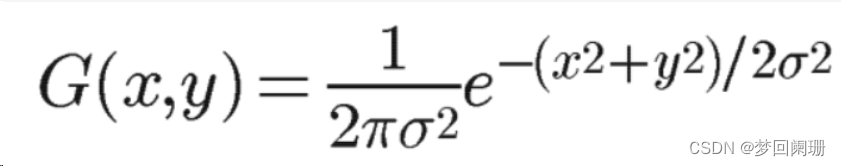
sigmaX和sigmaY該怎么取值？
如果 sigmaX 和 sigmaY 都設置為相同的值，那么高斯核將是一個圓形的，產生各向同性的模糊。這通常在需要保持圖像各向同性的情況下使用，比如去除噪聲或者平滑圖像。
如果 sigmaX 和 sigmaY 設置為不同的值，高斯核將呈橢圓形狀，產生各向異性的模糊。這可以在需要在圖像的不同方向上應用不同程度的模糊時使用。
具體的 sigmaX 和 sigmaY 的值可以根據圖像的特性來選擇。如果圖像中有較大的細節結構，可能需要較小的標準差來保留這些細節。相反，如果圖像中的結構比較平坦，可以使用較大的標準差進行更強烈的模糊。

高斯濾波后的圖像如下：

參考文章：【圖像處理】高斯模糊、高斯函數、高斯核、高斯卷積操作