Go語言實現深度學習的正向傳播和反向傳播

文章目錄

  • 開發前言
  • 開發理論
  • 圖解理論
  • 數據類型
  • 數學函數
  • 數據節點統一抽象
  • 變量數據節點
  • 常量數據節點
  • 單目運算封裝
  • 雙目運算封裝
  • 算子節點統一抽象
  • 基礎算子
  • 加法算子
  • 減法算子
  • 乘法算子
  • 除法算子
  • 指數算子
  • 對數算子
  • 正切算子
  • 正弦算子
  • 余弦算子
  • 數據流圖
  • 正向傳播
  • 反向傳播
  • 正向訓練
  • 反向訓練
  • 運行示例
  • 開發總結

開發前言

正向傳播是指從神經網絡的輸入層開始，通過逐層計算和傳遞，將輸入數據一直傳遞到輸出層。在每一層中，通過對輸入數據進行加權求和并應用激活函數，得到該層的輸出。這個過程可以看作是將輸入數據在網絡中前進（向前傳播），直至得到模型的預測結果。

反向傳播是指根據模型的預測結果和實際標簽之間的差異，從輸出層向輸入層反向計算梯度，并利用梯度來更新網絡參數。

這篇博客我將使用Go語言實現正向傳播和反向傳播，幫助你理解其底層的運轉規律

項目代碼使用純粹的Go語言標準庫實現，不借用任何其它第三方庫。用輪子是生活，造輪子是信仰。

我是醉墨居士，我們現在開始吧🤗

開發理論

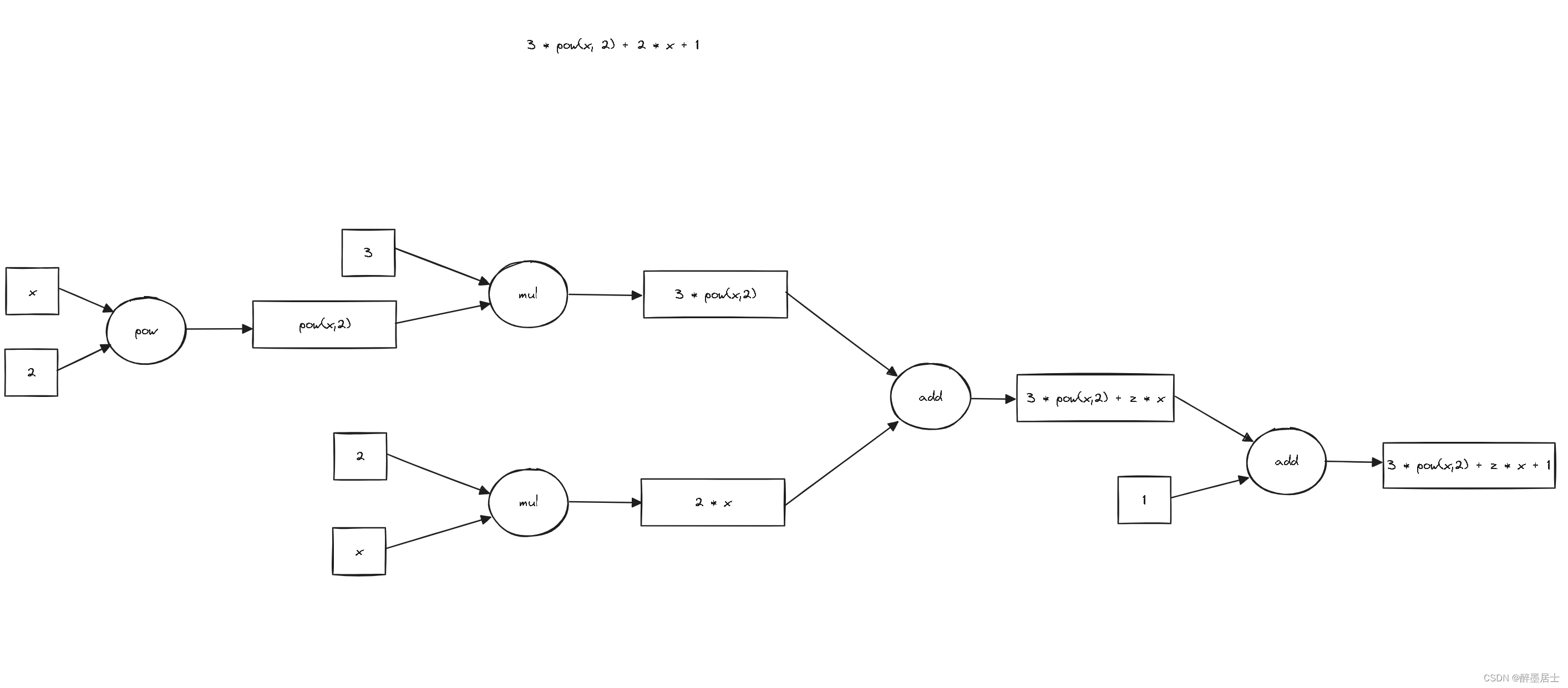
一個數學函數，由一系列數據和一系列運算方式構成，我們將數據對應為數據節點，將運算方式對應為算子節點，這樣我們就可以將數學函數轉化為由一系列數據節點和一系列算子節點組成的數據流圖

正向傳遞數據流圖，不斷運算數據，就是正向傳播的過程
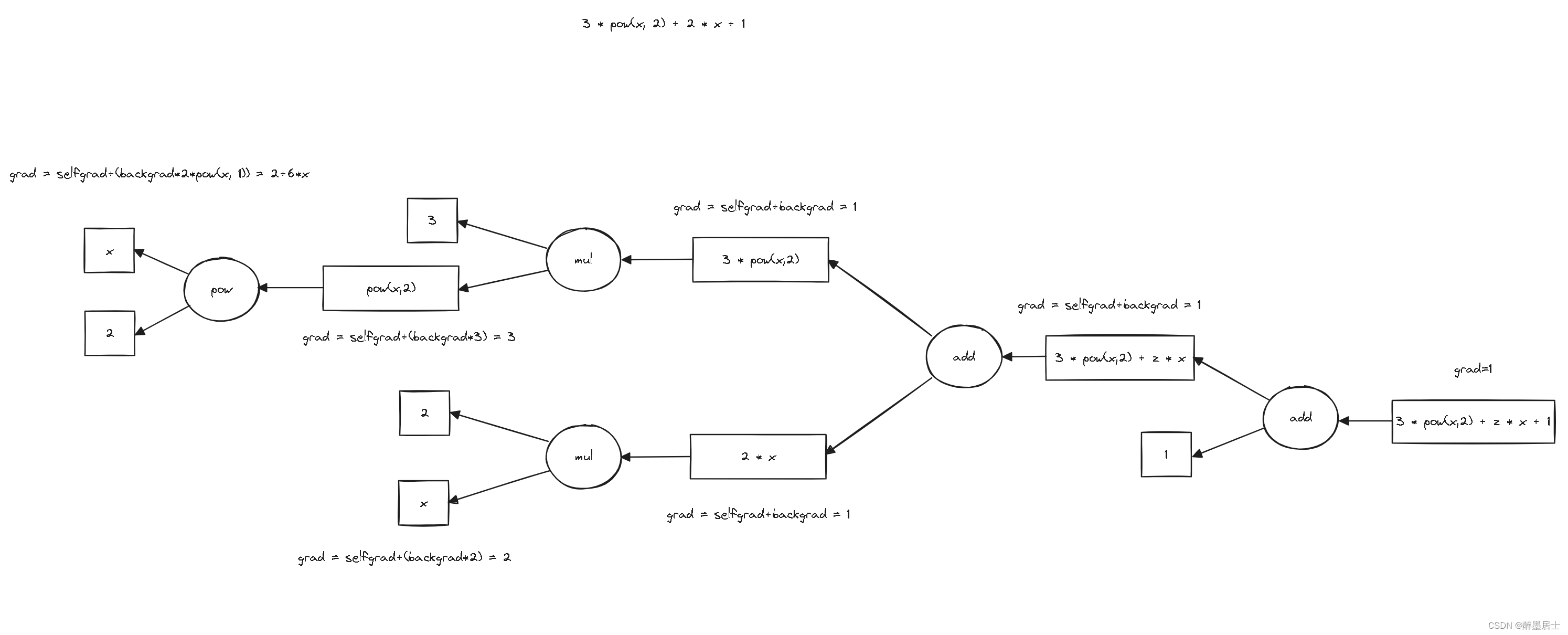
反向傳遞數據流圖，不斷累加梯度，就是反向傳播的過程

圖解理論

我畫了兩張圖來表示函數3 * pow(x, 2) + 2 * x + 1的正向傳播和反向傳播的過程

正向傳播圖解
forward

反向傳播圖解
backward

數據類型

data/type.go

package datatype Type interface {~int | ~int32 | ~int64 |~uint | ~uint32 | ~uint64 |~float32 | ~float64
}

數學函數

math/math.go

package mathimport ("dl/node"stmath "math"
)func Pow[T node.Type](a, b T) T {return T(stmath.Pow(float64(a), float64(b)))
}func Ln[T node.Type](a T) T {return T(stmath.Log(float64(a)))
}func Tan[T node.Type](a T) T {return T(stmath.Tan(float64(a)))
}func Sin[T node.Type](a T) T {return T(stmath.Sin(float64(a)))
}func Cos[T node.Type](a T) T {return T(stmath.Cos(float64(a)))
}

數據節點統一抽象

fm/datanode.go

type DataNode[T data.Type] interface {Data()TSetData(T)Grad()TsetGrad(T)preNode() CalNode[T]backNodes() *[]CalNode[T]fm()FlowMap[T]Add(DataNode[T]) DataNode[T]Sub(DataNode[T]) DataNode[T]Mul(DataNode[T]) DataNode[T]Div(DataNode[T]) DataNode[T]Pow(DataNode[T]) DataNode[T]Ln() DataNode[T]Tan() DataNode[T]Sin() DataNode[T]Cos() DataNode[T]
}

變量數據節點

package fmimport "dl/data"type varDataNode[T data.Type] struct {data Tgrad Tprenode CalNode[T]backnodes []CalNode[T]flowmap FlowMap[T]
}func (n *varDataNode[T]) Data() T {return n.data
}func (n *varDataNode[T]) SetData(i T) {n.data = i
}func (n *varDataNode[T]) Grad() T {return n.grad
}func (n *varDataNode[T]) setGrad(i T) {n.grad = i
}func (n *varDataNode[T]) preNode() CalNode[T] {return n.prenode
}func (n *varDataNode[T]) backNodes() *[]CalNode[T] {return &n.backnodes
}func (n *varDataNode[T]) fm() FlowMap[T] {return n.flowmap
}func (n *varDataNode[T]) Add(node DataNode[T]) DataNode[T] {return calTwo(newAdd[T](), n, node)
}func (n *varDataNode[T]) Sub(node DataNode[T]) DataNode[T] {return calTwo(newSub[T](), n, node)
}func (n *varDataNode[T]) Mul(node DataNode[T]) DataNode[T] {return calTwo(newMul[T](), n, node)
}func (n *varDataNode[T]) Div(node DataNode[T]) DataNode[T] {return calTwo(newDiv[T](), n, node)
}func (n *varDataNode[T]) Pow(node DataNode[T]) DataNode[T] {return calTwo(newPow[T](), n, node)
}func (n *varDataNode[T]) Ln() DataNode[T] {return calOne(newLn[T](), n)
}func (n *varDataNode[T]) Tan() DataNode[T] {return calOne(newTan[T](), n)
}func (n *varDataNode[T]) Sin() DataNode[T] {return calOne(newSin[T](), n)
}func (n *varDataNode[T]) Cos() DataNode[T] {return calOne(newCos[T](), n)
}

常量數據節點

type constDataNode[T data.Type] struct {data      Tprenode   CalNode[T]backnodes []CalNode[T]flowmap   FlowMap[T]
}func (n *constDataNode[T]) Data() T {return n.data
}func (n *constDataNode[T]) SetData(i T) {n.data = i
}
func (n *constDataNode[T]) Grad() T {return 0
}func (n *constDataNode[T]) setGrad(T) {}func (n *constDataNode[T]) preNode() CalNode[T] {return n.prenode
}func (n *constDataNode[T]) backNodes() *[]CalNode[T] {return &n.backnodes
}func (n *constDataNode[T]) fm() FlowMap[T] {return n.flowmap
}func (n *constDataNode[T]) Add(node DataNode[T]) DataNode[T] {return calTwo(newAdd[T](), n, node)
}func (n *constDataNode[T]) Sub(node DataNode[T]) DataNode[T] {return calTwo(newSub[T](), n, node)
}func (n *constDataNode[T]) Mul(node DataNode[T]) DataNode[T] {return calTwo(newMul[T](), n, node)
}func (n *constDataNode[T]) Div(node DataNode[T]) DataNode[T] {return calTwo(newDiv[T](), n, node)
}func (n *constDataNode[T]) Pow(node DataNode[T]) DataNode[T] {return calTwo(newPow[T](), n, node)
}func (n *constDataNode[T]) Ln() DataNode[T] {return calOne(newLn[T](), n)
}func (n *constDataNode[T]) Tan() DataNode[T] {return calOne(newTan[T](), n)
}func (n *constDataNode[T]) Sin() DataNode[T] {return calOne(newSin[T](), n)
}func (n *constDataNode[T]) Cos() DataNode[T] {return calOne(newCos[T](), n)
}

單目運算封裝

func calOne[T data.Type](operation CalNode[T], a DataNode[T]) DataNode[T] {*a.fm().calnodes = append(*a.fm().calnodes, operation)*a.backNodes() = append(*a.backNodes(), operation)res := &varDataNode[T]{prenode: operation,flowmap: a.fm(),}*a.fm().datanodes = append(*a.fm().datanodes, res)operation.CalNode().PreNodes = []DataNode[T]{a}operation.CalNode().BackNode = resreturn res
}

雙目運算封裝

func calTwo[T data.Type] (operation CalNode[T], a, b DataNode[T]) DataNode[T] {if a.fm() != b.fm() {return nil}*a.fm().calnodes = append(*a.fm().calnodes, operation)*a.backNodes() = append(*a.backNodes(), operation)*b.backNodes() = append(*b.backNodes(), operation)res := &varDataNode[T]{prenode: operation,flowmap: a.fm(),}*a.fm().datanodes = append(*a.fm().datanodes, res)operation.CalNode().PreNodes = []DataNode[T]{a, b}operation.CalNode().BackNode = resreturn res
}

算子節點統一抽象

fm/calnode.go

type CalNode[T data.Type] interface {CalNode() *BaseCalNode[T]Forward()Backward()
}

基礎算子

type BaseCalNode[T data.Type] struct {PreNodes []DataNode[T]BackNode DataNode[T]
}

加法算子

type AddNode[T data.Type] BaseCalNode[T]func newAdd[T data.Type]() CalNode[T] {basenode := &BaseCalNode[T]{}return (*AddNode[T])(basenode)
}func (n *AddNode[T]) CalNode() *BaseCalNode[T] {return (*BaseCalNode[T])(n)
}func (n *AddNode[T]) Forward() {n.BackNode.SetData(n.CalNode().PreNodes[0].Data() + n.CalNode().PreNodes[1].Data())
}func (n *AddNode[T]) Backward() {// selfgrad + backgradgrad0 := n.PreNodes[0].Grad() + n.BackNode.Grad()// selfgrad + backgradgrad1 := n.PreNodes[1].Grad() + n.BackNode.Grad()n.PreNodes[0].setGrad(grad0)n.PreNodes[1].setGrad(grad1)
}

減法算子

type SubNode[T data.Type] BaseCalNode[T]func newSub[T data.Type]() CalNode[T] {basenode := &BaseCalNode[T]{}return (*SubNode[T])(basenode)
}func (n *SubNode[T]) CalNode() *BaseCalNode[T] {return (*BaseCalNode[T])(n)
}func (n *SubNode[T]) Forward() {n.BackNode.SetData(n.CalNode().PreNodes[0].Data() - n.CalNode().PreNodes[1].Data())
}func (n *SubNode[T]) Backward() {// selfgrad + backgradgrad0 := n.PreNodes[0].Grad() + n.BackNode.Grad()// selfgrad - backgradgrad1 := n.PreNodes[1].Grad() - n.BackNode.Grad()n.PreNodes[0].setGrad(grad0)n.PreNodes[1].setGrad(grad1)
}

乘法算子

type MulNode[T data.Type] BaseCalNode[T]func newMul[T data.Type]() CalNode[T] {basenode := &BaseCalNode[T]{}return (*MulNode[T])(basenode)
}func (n *MulNode[T]) CalNode() *BaseCalNode[T] {return (*BaseCalNode[T])(n)
}func (n *MulNode[T]) Forward() {n.BackNode.SetData(n.CalNode().PreNodes[0].Data() * n.CalNode().PreNodes[1].Data())
}func (n *MulNode[T]) Backward() {a := n.PreNodes[0].Data()b := n.PreNodes[1].Data()backgrad := n.BackNode.Grad()// selfgrad + (backgrad * b)grad0 := n.PreNodes[0].Grad() + (backgrad * b)// selfgrad + (backgrad * a)grad1 := n.PreNodes[1].Grad() + (backgrad * a)n.PreNodes[0].setGrad(grad0)n.PreNodes[1].setGrad(grad1)
}

除法算子

type DivNode[T data.Type] BaseCalNode[T]func newDiv[T data.Type]() CalNode[T] {basenode := &BaseCalNode[T]{}return (*DivNode[T])(basenode)
}func (n *DivNode[T]) CalNode() *BaseCalNode[T] {return (*BaseCalNode[T])(n)
}func (n *DivNode[T]) Forward() {n.BackNode.SetData(n.CalNode().PreNodes[0].Data() / n.CalNode().PreNodes[1].Data())
}func (n *DivNode[T]) Backward() {a := n.PreNodes[0].Data()b := n.PreNodes[1].Data()backgrad := n.BackNode.Grad()// selfgrad + (backgrad / b)grad0 := n.PreNodes[0].Grad() + (backgrad / b)// selfgrad - (backgrad * a / pow(b, 2))grad1 := n.PreNodes[1].Grad() - (backgrad * a / math.Pow(b, 2))n.PreNodes[0].setGrad(grad0)n.PreNodes[1].setGrad(grad1)
}

指數算子

type PowNode[T data.Type] BaseCalNode[T]func newPow[T data.Type]() CalNode[T] {basenode := &BaseCalNode[T]{}return (*PowNode[T])(basenode)
}func (n *PowNode[T]) CalNode() *BaseCalNode[T] {return (*BaseCalNode[T])(n)
}func (n *PowNode[T]) Forward() {n.BackNode.SetData(math.Pow(n.CalNode().PreNodes[0].Data(), n.CalNode().PreNodes[1].Data()))
}func (n *PowNode[T]) Backward() {a := n.PreNodes[0].Data()b := n.PreNodes[1].Data()backgrad := n.BackNode.Grad()// selfgrad + (backgrad * b * pow(a, b-1))grad0 := n.PreNodes[0].Grad() + (backgrad * b * math.Pow(a, b-1))// selfgrad + (backgrad * pow(a, b) * ln(a))grad1 := n.PreNodes[1].Grad() + (backgrad * math.Pow(a, b) * math.Ln(a))n.PreNodes[0].setGrad(grad0)n.PreNodes[1].setGrad(grad1)
}

對數算子

type LnNode[T data.Type] BaseCalNode[T]func newLn[T data.Type]() CalNode[T] {basenode := &BaseCalNode[T]{}return (*LnNode[T])(basenode)
}func (n *LnNode[T]) CalNode() *BaseCalNode[T] {return (*BaseCalNode[T])(n)
}func (n *LnNode[T]) Forward() {n.BackNode.SetData(math.Ln(n.CalNode().PreNodes[0].Data()))
}func (n *LnNode[T]) Backward() {a := n.PreNodes[0].Data()backgrad := n.BackNode.Grad()// selfgrad + (backgrad / a)grad0 := n.PreNodes[0].Grad() + (backgrad / a)n.PreNodes[0].setGrad(grad0)
}

正切算子

type TanNode[T data.Type] BaseCalNode[T]func newTan[T data.Type]() CalNode[T] {basenode := &BaseCalNode[T]{}return (*TanNode[T])(basenode)
}func (n *TanNode[T]) CalNode() *BaseCalNode[T] {return (*BaseCalNode[T])(n)
}func (n *TanNode[T]) Forward() {n.BackNode.SetData(math.Tan(n.CalNode().PreNodes[0].Data()))
}func (n *TanNode[T]) Backward() {a := n.PreNodes[0].Data()backgrad := n.BackNode.Grad()// selfgrad + (backgrad / pow(cos(a), 2))grad0 := n.PreNodes[0].Grad() + (backgrad / math.Pow(math.Cos(a), 2))n.PreNodes[0].setGrad(grad0)
}

正弦算子

type SinNode[T data.Type] BaseCalNode[T]func newSin[T data.Type]() CalNode[T] {basenode := &BaseCalNode[T]{}return (*SinNode[T])(basenode)
}func (n *SinNode[T]) CalNode() *BaseCalNode[T] {return (*BaseCalNode[T])(n)
}func (n *SinNode[T]) Forward() {n.BackNode.SetData(math.Sin(n.CalNode().PreNodes[0].Data()))
}func (n *SinNode[T]) Backward() {a := n.PreNodes[0].Data()backgrad := n.BackNode.Grad()// selfgrad + (backgrad * cos(a))grad0 := n.PreNodes[0].Grad() + (backgrad * math.Cos(a))n.PreNodes[0].setGrad(grad0)
}

余弦算子

type CosNode[T data.Type] BaseCalNode[T]func newCos[T data.Type]() CalNode[T] {basenode := &BaseCalNode[T]{}return (*CosNode[T])(basenode)
}func (n *CosNode[T]) CalNode() *BaseCalNode[T] {return (*BaseCalNode[T])(n)
}func (n *CosNode[T]) Forward() {n.BackNode.SetData(math.Cos(n.CalNode().PreNodes[0].Data()))
}func (n *CosNode[T]) Backward() {a := n.PreNodes[0].Data()backgrad := n.BackNode.Grad()// selfgrad - (backgrad * sin(a))grad0 := n.PreNodes[0].Grad() - (backgrad * math.Sin(a))n.PreNodes[0].setGrad(grad0)
}

數據流圖

fm/flowmap.go

type FlowMap[T data.Type] struct {calnodes  *[]CalNode[T]datanodes *[]DataNode[T]
}func NewFlowMap[T data.Type]() *FlowMap[T] {calnodes := make([]CalNode[T], 0)datanods := make([]DataNode[T], 0)return &FlowMap[T]{calnodes:  &calnodes,datanodes: &datanods,}
}func (m FlowMap[T]) NewData() DataNode[T] {node := &varDataNode[T]{backnodes: make([]CalNode[T], 0),flowmap:   m,}*m.datanodes = append(*m.datanodes, node)return node
}func (m FlowMap[T]) NewConstData(i T) DataNode[T] {return &constDataNode[T]{backnodes: make([]CalNode[T], 0),data:      i,flowmap:   m,}
}

正向傳播

func (m FlowMap[T]) Forward() {n := len(*m.calnodes)for i := 0; i < n; i++ {(*m.calnodes)[i].Forward()}
}

反向傳播

func (m FlowMap[T]) Backward() {for i := len(*m.datanodes) - 1; i >= 0; i-- {(*m.datanodes)[i].setGrad(0)}n := len(*m.calnodes)-1(*m.calnodes)[n].CalNode().BackNode.setGrad(1)for i := n; i >= 0; i-- {(*m.calnodes)[i].Backward()}
}

正向訓練

func (m FlowMap[T]) ForwardWalk(step T) {for i := len(*m.datanodes) - 1; i >= 0; i-- {(*m.datanodes)[i].SetData((*m.datanodes)[i].Data() + (*m.datanodes)[i].Grad() * step)}
}

反向訓練

func (m FlowMap[T]) BackwardWalk(step T) {for i := len(*m.datanodes) - 1; i >= 0; i-- {(*m.datanodes)[i].SetData((*m.datanodes)[i].Data() - (*m.datanodes)[i].Grad() * step)}
}

運行示例

我們的運行示例使用理論圖解的那個例子： 3 * pow(x, 2) + 2 * x + 1

// 3 * pow(x, 2) + 2 * x + 1
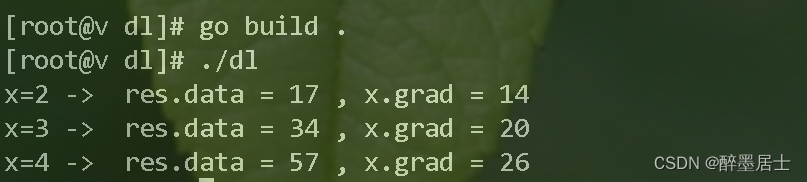
func main() {m := fm.NewFlowMap[float64]()x := m.NewData()three := m.NewConstData(3)two := m.NewConstData(2)one := m.NewConstData(1)res := three.Mul(x.Pow(two)).Add(two.Mul(x)).Add(one)x.SetData(2)m.Forward()m.Backward()// data = 3 * pow(2, 2) + 2 * 2 + 1 = 17// grad = 2 + 6 * x = 14fmt.Println("x=2 -> ", "res.data =", res.Data(), ",", "x.grad =", x.Grad())x.SetData(3)m.Forward()m.Backward()// data = 3 * pow(3, 2) + 2 * 3 + 1 = 34// grad = 2 + 6 * x = 20fmt.Println("x=3 -> ", "res.data =", res.Data(), ",", "x.grad =", x.Grad())x.SetData(4)m.Forward()m.Backward()// data = 3 * pow(4, 2) + 2 * 4 + 1 = 57// grad = 2 + 6 * x = 26fmt.Println("x=4 -> ", "res.data =", res.Data(), ",", "x.grad =", x.Grad())
}

運行結果
result

開發總結

恭喜你，我們一起使用Go語言完成了深度學習的正向傳播和反向傳播，希望這個項目能讓你有所收獲😊

我的特色就是用最簡單的方式幫助你學會最硬核的知識，一起加油吧??

我是醉墨居士，之前這個賬號改了好幾次名稱，從此之后這個賬號的名稱大概率不會再變動😜

如果有什么錯誤，請你評論區或者私信我指出，讓我們一起進步??

請你多多關注我，開發這個項目，并且整理總結，花費了很多的精力，博客熱度越高，更新速度越快😎

本文來自互聯網用戶投稿，該文觀點僅代表作者本人，不代表本站立場。本站僅提供信息存儲空間服務，不擁有所有權，不承擔相關法律責任。
如若轉載，請注明出處：http://www.pswp.cn/news/207174.shtml
繁體地址，請注明出處：http://hk.pswp.cn/news/207174.shtml
英文地址，請注明出處：http://en.pswp.cn/news/207174.shtml

如若內容造成侵權/違法違規/事實不符，請聯系多彩編程網進行投訴反饋email:809451989@qq.com，一經查實，立即刪除！

相關文章

我的記事本

我的記事本

url uniform resource locator. 統一資源定位符 請求狀態碼 1XX:信息響應 2XX:成功響應 3XX:重定向消息 4XX:客戶端錯誤響應 5XX:服務器端錯誤響應 IP地址分類 本機回環IP地址&#xff1a;127.0.0.1 &#xff5e; 127.255.255.254 局域網IP(私網IP) 192.168.0.0 &am…
閱讀更多...
船舶機電設備振動數據采集監控系統解決方案

船舶機電設備振動數據采集監控系統解決方案

船舶運行中&#xff0c;通常需要通過振動數據采集系統對船舶的各個機電設備運行進行監控&#xff0c;有助于在設備故障時快速預警&#xff0c;進行診斷、分析和維護&#xff0c;保證船舶機電設備正常工作&#xff0c;從而確保工作人員及船舶的安全。 船舶各種機電設備會產生大…
閱讀更多...
vLLM介紹

vLLM介紹

簡介 vLLM 工程github地址 Paged attention論文地址 vLLM開發者介紹 Woosuk Kwon vLLM: A high-throughput and memory-efficient inference and serving engine for LLMs. SkyPilot: A framework for easily and cost effectively running machine learning workloads on …
閱讀更多...
【模型量化】神經網絡量化基礎及代碼學習總結

【模型量化】神經網絡量化基礎及代碼學習總結

1 量化的介紹 量化是減少神經網絡計算時間和能耗的最有效的方法之一。在神經網絡量化中&#xff0c;權重和激活張量存儲在比訓練時通常使用的16-bit或32-bit更低的比特精度。當從32-bit降低到8-bit&#xff0c;存儲張量的內存開銷減少了4倍&#xff0c;矩陣乘法的計算成本則二…
閱讀更多...
ALNS算法中隨機化重要性的評價

ALNS算法中隨機化重要性的評價

文章概述 本研究分析了在海上提貨和交付問題中使用的ALNS元啟發式算法中的隨機化成分。研究者提出了簡單的確定性替代方案&#xff0c;并通過實驗比較了隨機化和確定性成分的性能。結果表明&#xff0c;初始實現的簡單確定性替代方案能夠與隨機化成分的性能相匹配。這項研究為…
閱讀更多...
IDEA使用git從遠程倉庫獲取項目

IDEA使用git從遠程倉庫獲取項目

將地址填入url中 然后直接clone就行
閱讀更多...
《Easy3d+Qt+VTK》學習

《Easy3d+Qt+VTK》學習

《Easy3dQtVTK》學習-1、編譯與配置 一、編譯二、配置注 一、編譯 1、 資源下載&#xff1a;easy3d giuhub 2、解壓縮 3、用qt打開CMakeLists.txt即可 4、點擊項目&#xff0c;選擇debug或者release&#xff0c;圖中3處可自行選擇&#xff0c;因為我的qt版本是6&#xff0c…
閱讀更多...
Java集合大總結——Collections工具類

Java集合大總結——Collections工具類

簡單闡述 參考操作數組的工具類&#xff1a;Arrays&#xff0c;Collections 是一個操作 Set、List 和 Map 等集合的工具類。 常用方法 Collections 中提供了一系列靜態的方法對集合元素進行排序、查詢和修改等操作&#xff0c;還提供了對集合對象設置不可變、對集合對象實現…
閱讀更多...
jdbc4.MySQLSyntaxErrorException: Query was empty

jdbc4.MySQLSyntaxErrorException: Query was empty

出現這種異常的原因&#xff0c;有幾個要點 檢查sql語句是否正確檢查你的條件是否真的被sql使用 背景 delete sql在xml中&#xff0c;賦值list對象&#xff0c;計劃進行批量刪除的sql&#xff0c;這時出現了異常&#xff0c;檢查后&#xff0c;發現這個list竟然是空&#xff…
閱讀更多...
Linux下的軟硬鏈接

Linux下的軟硬鏈接

Linux下的軟硬鏈接 Linux下的硬鏈接和軟鏈接是一種文件系統級別的鏈接方式&#xff0c;它們允許你在不同的目錄中創建指向同一個文件的引用。硬鏈接和軟鏈接的主要區別在于它們的實現方式和刪除方式。 硬鏈接&#xff08;Hard Link&#xff09;&#xff1a; 硬鏈接是指向同一…
閱讀更多...
在linux上如何運用虛擬數據優化器VDO

在linux上如何運用虛擬數據優化器VDO

本章主要介紹虛擬化數據優化器。 什么是虛擬數據優化器VDO 創建VDO設備以節約硬盤空間 16.1 了解什么是VDO VDO全稱是Virtual Data Optimize&#xff08;虛擬數據優化)&#xff0c;主要是為了節省硬盤空間。 現在假設有兩個文件file1和 file2&#xff0c;大小都是10G。file…
閱讀更多...
cpu 300% 爆滿 內存占用不高 排查

cpu 300% 爆滿 內存占用不高 排查

top查詢 cpu最高的PID ps -ef | grep PID 查看具體哪一個jar服務 jstack -l PID > ./jstack.log 下載/打印進程的線程棧信息 可以加信息簡單分析 或進一步 查看堆內存使用情況 jmap -heap Java進程id jstack.log 信息示例 Full thread dump Java HotSpot(TM) 64-Bit Se…
閱讀更多...
橫向擴展統一存儲與備份服務器功能

橫向擴展統一存儲與備份服務器功能

Infortrend 更新了GS&#xff0c;GSe&#xff0c;GSe Pro統一存儲系列的備份服務器功能。該功能降低數據備份成本&#xff0c;并提供靈活的備份策略。通過備份服務器功能&#xff0c;用戶可以通過多種途徑實現數據備份&#xff0c;包括公有云&#xff08;兼容S3&#xff09;、文…
閱讀更多...
為內核新增字符驅動模塊

為內核新增字符驅動模塊

1. 放置代碼 在./source/driver/char下放置模塊文件夾 2. Makefile和Kconfig makefile文件參考 obj-$(AAA_LED) AAA-led.oKconfig文件參考 config AAA_LEDtristate "Phytium macb led control module"depends on XXXdefault mhelpIf you have a n…
閱讀更多...
C/C++，樹算法——二叉樹的插入(Insert)算法之源程序

C/C++，樹算法——二叉樹的插入(Insert)算法之源程序

1 文本格式 #include<iostream> using namespace std; // A BTree node class BTreeNode { int* keys; // An array of keys int t; // Minimum degree (defines the range for number of keys) BTreeNode** C; // An array of child pointers int …
閱讀更多...
.NET中有多少種定時器

.NET中有多少種定時器

.NET中至少有6種定時器&#xff0c;每一種定時器都有它的用途和特點。根據定時器的應用場景&#xff0c;可以分為UI相關的定時器和UI無關的定時器。本文將簡單介紹這6種定時器的基本用法和特點。 UI定時器 .NET中的UI定時器主要是WinForm、WPF以及WebForm中的定時器。分別為&am…
閱讀更多...
dell服務器重啟后顯示器黑屏

dell服務器重啟后顯示器黑屏

1.硬件層面&#xff1a;觀察主機的指示燈 &#xff08;1&#xff09;指示燈偏黃&#xff0c;硬件存在問題&#xff08;內存條有靜電&#xff0c;拔出后用橡皮擦擦拭&#xff1b;或GPU松動&#xff09; a.電源指示燈黃&#xff0c;閃爍三下再閃爍一下&#xff0c;扣下主板上的紐…
閱讀更多...
Python Appium Selenium 查殺進程的實用方法

Python Appium Selenium 查殺進程的實用方法

一、前置說明 在自動化過程中&#xff0c;經常需要在命令行中執行一些操作&#xff0c;比如啟動應用、查殺應用等&#xff0c;因此可以封裝成一個CommandExecutor來專門處理這些事情。 二、操作步驟 # cmd_util.pyimport logging import os import platform import shutil i…
閱讀更多...
Java編程中通用的正則表達式（二）

Java編程中通用的正則表達式（二）

正則表達式&#xff0c;又稱正則式、規則表達式、正規表達式、正則模式或簡稱正則&#xff0c;是一種用來匹配字符串的工具。它是一種字符串模式的表示方法&#xff0c;可以用來檢索、替換和驗證文本。正則表達式是一個字符串&#xff0c;它描述了一些字符的組合&#xff0c;這…
閱讀更多...
dockers安裝rabbitmq

dockers安裝rabbitmq

RabbitMQ: easy to use, flexible messaging and streaming — RabbitMQhttps://www.rabbitmq.com/ Downloading and Installing RabbitMQ — RabbitMQ docker run -it --rm --name rabbitmq -p 5672:5672 -p 15672:15672 rabbitmq:3.12-management 之后參照&#xff1a;dock…
閱讀更多...
最新文章

Copyright @ 2022~2023