一、含義

線性索引，顧名思義就是說把圖像矩陣展平，相當于變成一維的圖像數組，故像素點的線性索引就是其在圖像數組中的索引值

行列號索引，對于一個二維的圖像矩陣有行有列，知道行號和列號就可以唯一確定一個點的位置，類似于二維的坐標（橫坐標，縱坐標）

下面舉個例子來具體地闡述一下線性索引和行列號索引的含義：

例如，有一張大小為 100x100 的灰度圖，那么可以用一個二維的圖像矩陣來表示，也就是100行100列的矩陣，如下圖所示：

綜上所述就是關于線性索引和行列號索引的簡要介紹，下面我們再來討論一下線性索引和行列號索引之間如何相互轉換？

二、線性索引轉換為行列號索引

可以使用 Python 的整除 ( // )和取余( % )運算

在進行轉換的講解之前，我們要先知道二維矩陣（此處以二維矩陣為例）是按照什么方式進行數據存儲的，也就是說是行優先存儲還是列優先存儲。

1.行優先存儲

含義：元素先存滿第一行后再存儲第二行，也就是第一行所有的元素都在第二行之前

假設有一個n行m列的矩陣以及一個線性索引index，可以用下面的代碼轉換線性索引為行列號索引：

rows = n  # 矩陣行數
cols = m  # 矩陣列數
index = index  # 線性索引#計算行列索引
row_index = index // cols  # 取商
col_index = index % cols   # 取余print("Row index:",row_index)
print("Column index:",col_index)

這段代碼首先使用整除運算 // 計算行索引，然后使用取余運算 % 計算列索引

這是因為在行優先的二維矩陣中，每存儲cols個元素，行數就增加1（注意：在Python中行號和列號都是從0開始的）

2.列優先存儲

含義：元素先存滿第一列后再存儲第二列，也就是第一列所有的元素都在第二列之前

接著上面的例子來進行講解，列優先存儲就要先計算列號，然后通過余數計算行號

rows = n  # 矩陣行數
cols = m  # 矩陣列數
index = index  # 線性索引#計算行列索引
col_index = index // rows  # 取商
row_index = index % rows   # 取余print("Row index:",row_index)
print("Column index:",col_index)

這段代碼首先使用整除運算 // 計算列索引，然后使用取余運算 % 計算行索引

這是因為在列優先的二維矩陣中，每存儲rows個元素，列數就增加1（注意：在Python中行號和列 號都是從0開始的）

3. 行優先和列優先存儲的差異

下面我們再來看看對于同一個點進行 行優先存儲 和 列優先存儲 的區別：

?

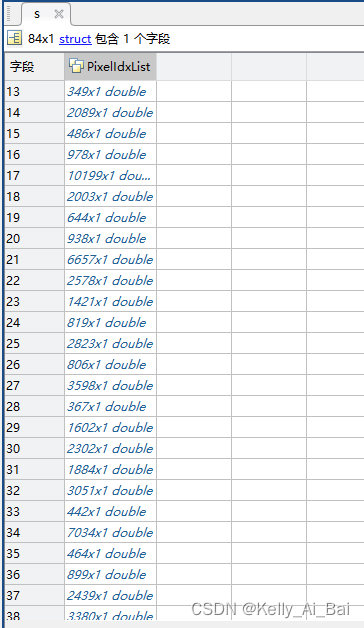
其中，region_edge_s.mat 是存儲了如上圖二值圖像所示的連通域，屬于每個連通域點的線性索引信息的Matlab文件，并且是以結構體形式存儲的，如下圖所示：

?

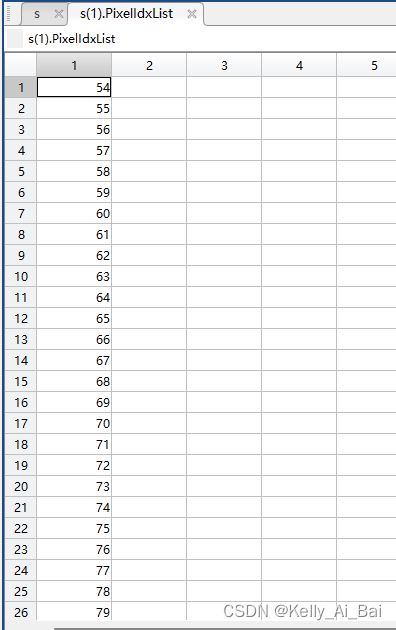
下面我們來將存儲在文件中的線性索引轉換為對應圖像中的行列號索引，經過上圖所示文件的讀取操作后，field變量已經將連通域中點的線性索引進行了保存。

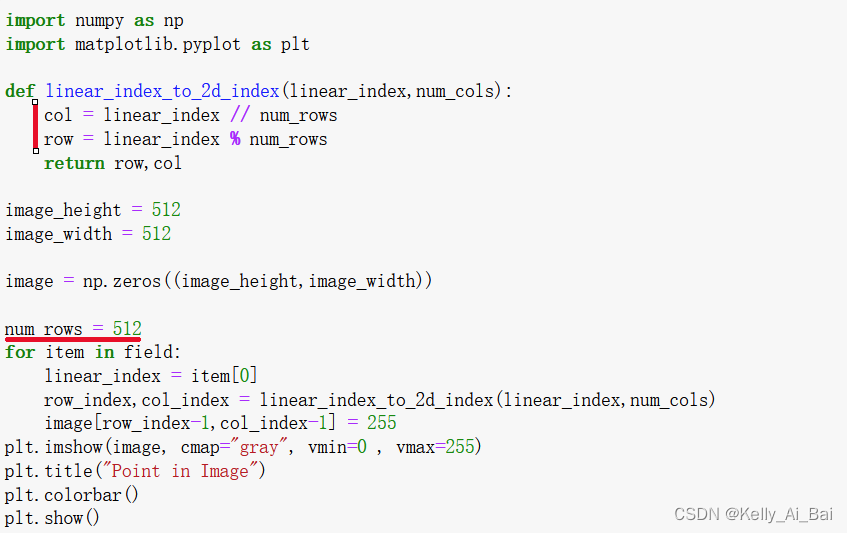
首先定義了一個函數 linear_index_to_2d_index ，此函數接受線性索引 linear_index 和 列數 num_cols 作為參數，計算行號和列號并進行返回

然后新建了一個大小為512x512的全零圖像矩陣image（初始的圖像為全黑），將得到的行號和列號所對應的位置處的像素值置為255（也就是以白色來顯示）

最后使用matplotlib庫來繪制圖像image，代碼以及運行結果如下圖所示：

• 按列優先存儲：

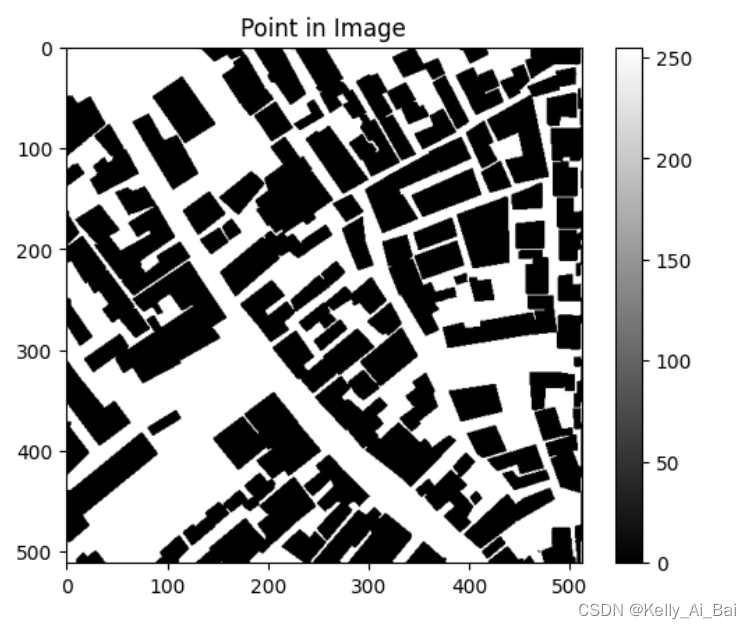
• 按行優先存儲

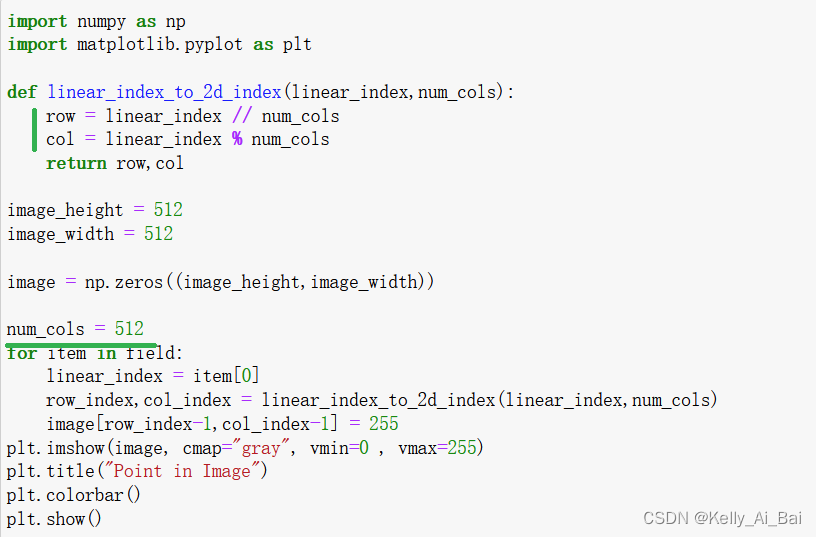
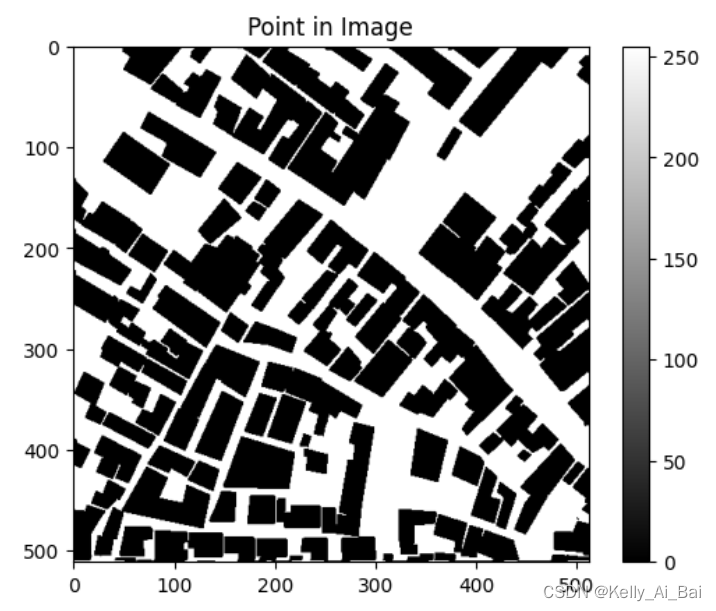
綜上所如圖所示，可以很清楚地看到? 按行存儲 和 按列存儲 之間的差異。

注意：?? 在這個例子中，可以看到? 按列存儲? 圖像可以得到和原始圖像一樣的結果，?? 這說明文件 region_edge_s.mat 中的線性索引是按列存儲的。因為 Matlab是按照列優先的原則存儲元素。所以在進行線性索引轉換行列號索引的時候，一定要清楚該圖像是按行存儲的信息還是按列存儲的。

?三、行列號索引轉換為線性索引

將行列號索引轉換為線性索引的方法取決于如何排列數據（按行存儲的數據還是按列存儲的數據）

下面舉個 按行存儲 的行列號轉換為線性索引 的例子：

一般情況下，對于二維矩陣或數組，行列號索引可以轉換為線性索引的公式如下：

假設有一個矩陣或數組，行數為 num_rows，列數為 num_cols，行索引為 row_index，列索引為 col_index，那么線性索引可以通過以下公式計算：

線性索引 = row_index * num_cols + col_index

這個公式基于矩陣在內存中的布局方式。行索引乘以列數得到的值代表了前面所有行占據的位置數量，再加上列索引得到具體位置的偏移量。

假設有一個3x3的矩陣，要將行列索引轉換為線性索引：

num_rows = 3
num_cols = 3
row_index = 1
col_index = 2linear_index = row_index * num_cols + col_index
print("線性索引:", linear_index)

• 在這個例子中，當 row_index 為 1，col_index 為 2 時，根據公式計算得到線性索引為 5

  同樣，如果要從線性索引計算出行列索引，可以使用以下公式：

  row_index = linear_index // num_cols
  col_index = linear_index % num_cols

  這樣就可以根據需要在行列索引和線性索引之間進行轉換