Q1將有序數組轉換為二叉搜索樹
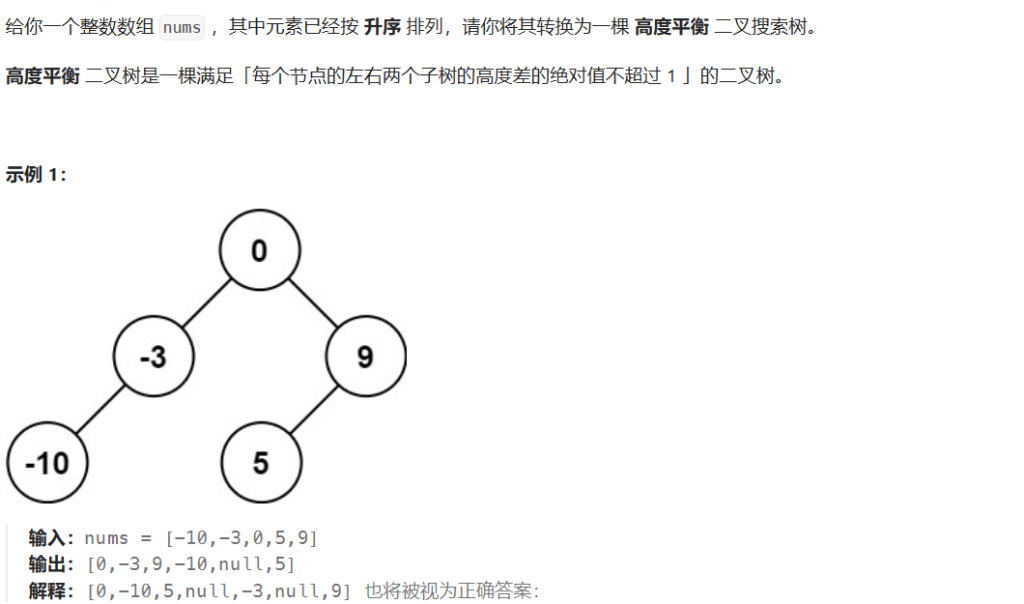
題目大致意思就是從一個數組建立平衡的二叉搜索樹。由于數組以及進行了升序處理，我們只要考慮好怎么做到平衡的。平衡意味著左右子樹的高度差不能大于1。由此我們可以想著是否能用類似二分+遞歸來解決。
如果left>right,直接返回nullpter
否則 mid = (left + right) / 2,將a[mid]值賦給root結點
遞歸左子樹 right = mid-1;
遞歸右子樹left = mid+1;
這樣一來問題就得到了解決。
class Solution {
public:TreeNode* sortedArrayToBST(vector<int>& nums) {return build(nums,0,nums.size() - 1);}TreeNode*build(vector<int>&nums,int left,int right){if(left > right)return nullptr;int mid = (left + right) / 2;TreeNode*root = new TreeNode(nums[mid]);root->left = build(nums,left,mid-1);root->right = build(nums,mid+1,right);return root; }
};Q2路徑總和
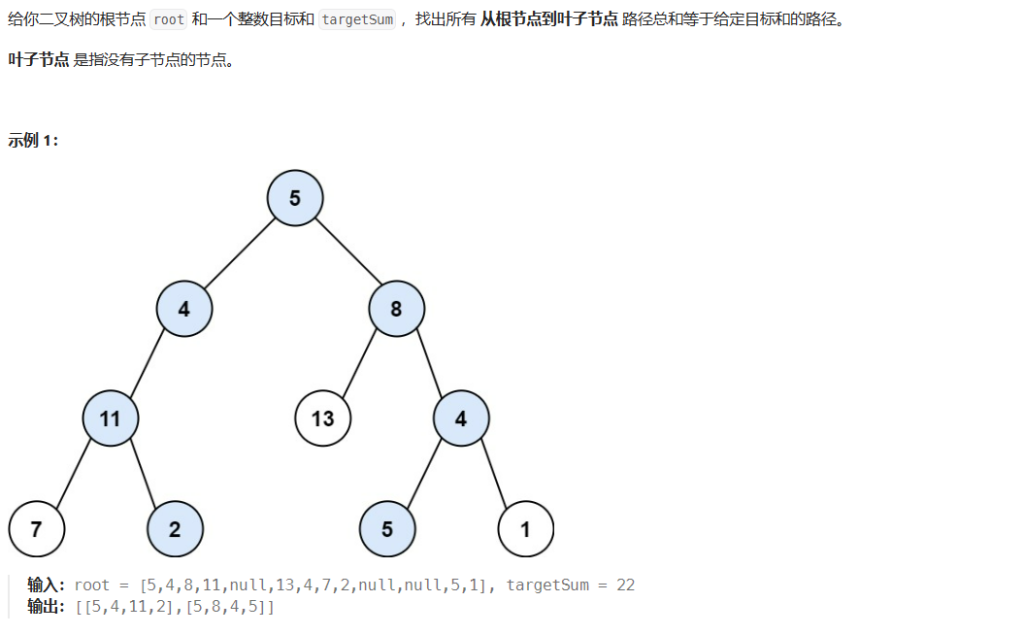本題是經典的搜索回溯+路徑記錄的題目。
路徑記錄:
先序進行遞歸遍歷，進行路徑更新
如果當前sum = root->val,將次路徑添加到答案中
搜索回溯:
遞推參數： 當前節點 root ，當前目標值 tar
終止條件： 若節點 root 為空，則直接返回。
遞推工作：
路徑更新： 將當前節點值 root.val 加入路徑 path 。
目標值更新： tar = tar - root.val（即目標值 tar 從 targetSum 減至 0 ）
路徑記錄： 當 (1) root 為葉節點 且 (2) 路徑和等于目標值 ，則將此路徑 path 加入 res 。
先序遍歷： 遞歸左 / 右子節點。
路徑恢復： 向上回溯前，需要將當前節點從路徑 path 中刪除，即執行 path.pop_back() 。
class Solution { public:vector<vector<int>> ret;vector<int> path;void dfs(TreeNode*root,int targetSum){if(root==nullptr)return;path.push_back(root->val);if(root->left == nullptr && root->right == nullptr){if(targetSum == root->val)ret.push_back(path);}dfs(root->left,targetSum-root->val);dfs(root->right,targetSum-root->val);path.pop_back();}vector<vector<int>> pathSum(TreeNode* root, int targetSum) {dfs(root,targetSum);return ret;} };本文由博客一文多發平臺 OpenWrite 發布！
