Every day a Leetcode
題目來源:200. 島嶼數量
解法1:深度優先搜索
設目前指針指向一個島嶼中的某一點 (i, j),尋找包括此點的島嶼邊界。
從 (i, j) 向此點的上下左右 (i+1,j),(i-1,j),(i,j+1),(i,j-1) 做深度搜索。
終止條件:
- (i, j) 越過矩陣邊界;
- grid[i][j] == 0,代表此分支已越過島嶼邊界。
搜索島嶼的同時,執行 grid[i][j] = ‘0’,即將島嶼所有節點刪除,以免之后重復搜索相同島嶼。
遍歷整個矩陣,當遇到 grid[i][j] == ‘1’ 時,從此點開始做深度優先搜索 dfs,島嶼數 count + 1 且在深度優先搜索中刪除此島嶼。
最終返回島嶼數 count 即可。
代碼:
/** @lc app=leetcode.cn id=200 lang=cpp** [200] 島嶼數量*/// @lc code=start// 深度優先搜索class Solution
{
private:const int dx[4] = {-1, 0, 1, 0};const int dy[4] = {0, 1, 0, -1};public:int numIslands(vector<vector<char>> &grid){if (grid.empty())return 0;int m = grid.size(), n = m ? grid[0].size() : 0;int islands = 0;for (int i = 0; i < m; i++)for (int j = 0; j < n; j++)if (grid[i][j] == '1'){islands++;dfs(grid, i, j);}return islands;}// 輔函數 - 深度優先搜索void dfs(vector<vector<char>> &grid, int r, int c){if (r < 0 || r >= grid.size() || c < 0 || c >= grid[0].size() || grid[r][c] == '0')return;grid[r][c] = '0';for (int i = 0; i < 4; i++){int x = dx[i], y = dy[i];dfs(grid, r + x, c + y);}}
};
// @lc code=end
結果:
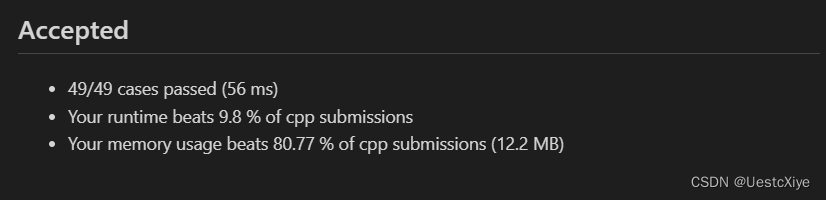
復雜度分析:
時間復雜度:O(m*n),其中 m 和 n 分別是二維數組 grid 的行數和列數。
空間復雜度:O(m*n),其中 m 和 n 分別是二維數組 grid 的行數和列數。在最壞情況下,整個網格均為陸地,深度優先搜索的深度達到 m*n。
解法2:廣度優先搜索
同樣地,我們也可以使用廣度優先搜索代替深度優先搜索。
為了求出島嶼的數量,我們可以掃描整個二維網格。如果一個位置為 1,則將其加入隊列,開始進行廣度優先搜索。在廣度優先搜索的過程中,每個搜索到的 1 都會被重新標記為 0。直到隊列為空,搜索結束。
最終島嶼的數量就是我們進行廣度優先搜索的次數。
代碼:
class Solution
{
public:int numIslands(vector<vector<char>> &grid){if (grid.empty())return 0;int m = grid.size(), n = m ? grid[0].size() : 0;int islands = 0;for (int r = 0; r < m; r++)for (int c = 0; c < n; c++)if (grid[r][c] == '1'){islands++;grid[r][c] = '0';queue<pair<int, int>> neighbors;neighbors.push({r, c});while (!neighbors.empty()){auto rc = neighbors.front();neighbors.pop();int row = rc.first, col = rc.second;if (row - 1 >= 0 && grid[row - 1][col] == '1'){neighbors.push({row - 1, col});grid[row - 1][col] = '0';}if (row + 1 < m && grid[row + 1][col] == '1'){neighbors.push({row + 1, col});grid[row + 1][col] = '0';}if (col - 1 >= 0 && grid[row][col - 1] == '1'){neighbors.push({row, col - 1});grid[row][col - 1] = '0';}if (col + 1 < n && grid[row][col + 1] == '1'){neighbors.push({row, col + 1});grid[row][col + 1] = '0';}}}return islands;}
};
結果:
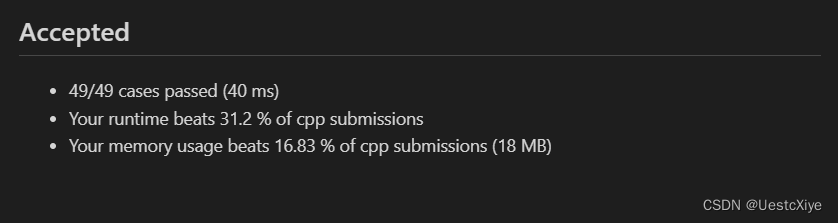
復雜度分析:
時間復雜度:O(m*n),其中 m 和 n 分別是二維數組 grid 的行數和列數。
空間復雜度:O(min?(m, n)),其中 m 和 n 分別是二維數組 grid 的行數和列數。在最壞情況下,整個網格均為陸地,隊列的大小可以達到 min?(m, n)。
解法3:并查集
同樣地,我們也可以使用并查集代替搜索。
為了求出島嶼的數量,我們可以掃描整個二維網格。如果一個位置為 1,則將其與相鄰四個方向上的 1 在并查集中進行合并。
最終島嶼的數量就是并查集中連通分量的數目。
代碼:
class UnionFind {
public:UnionFind(vector<vector<char>>& grid) {count = 0;int m = grid.size();int n = grid[0].size();for (int i = 0; i < m; ++i) {for (int j = 0; j < n; ++j) {if (grid[i][j] == '1') {parent.push_back(i * n + j);++count;}else {parent.push_back(-1);}rank.push_back(0);}}}int find(int i) {if (parent[i] != i) {parent[i] = find(parent[i]);}return parent[i];}void unite(int x, int y) {int rootx = find(x);int rooty = find(y);if (rootx != rooty) {if (rank[rootx] < rank[rooty]) {swap(rootx, rooty);}parent[rooty] = rootx;if (rank[rootx] == rank[rooty]) rank[rootx] += 1;--count;}}int getCount() const {return count;}private:vector<int> parent;vector<int> rank;int count;
};class Solution {
public:int numIslands(vector<vector<char>>& grid) {int nr = grid.size();if (!nr) return 0;int nc = grid[0].size();UnionFind uf(grid);int num_islands = 0;for (int r = 0; r < nr; ++r) {for (int c = 0; c < nc; ++c) {if (grid[r][c] == '1') {grid[r][c] = '0';if (r - 1 >= 0 && grid[r-1][c] == '1') uf.unite(r * nc + c, (r-1) * nc + c);if (r + 1 < nr && grid[r+1][c] == '1') uf.unite(r * nc + c, (r+1) * nc + c);if (c - 1 >= 0 && grid[r][c-1] == '1') uf.unite(r * nc + c, r * nc + c - 1);if (c + 1 < nc && grid[r][c+1] == '1') uf.unite(r * nc + c, r * nc + c + 1);}}}return uf.getCount();}
};
復雜度分析:











并使用Trino訪問Minio)







)
)