Ma M, Ren J, Zhao L, et al. Smil: Multimodal learning with severely missing modality[C]//Proceedings of the AAAI Conference on Artificial Intelligence. 2021, 35(3): 2302-2310.[開源]
本文的核心思想是探討和解決多模態學習中的一個重要問題:在訓練和測試數據中嚴重缺失某些模態時,如何有效進行學習。具體來說,這里的“嚴重缺失”指的是在多達90%的訓練樣本中缺少一些模態信息。在過去的研究中,大多關注于如何處理測試數據的模態不完整性,而對于訓練數據的模態不完整性,尤其是嚴重缺失的情況,探討較少。文章提出了一種新的方法——SMIL(Severely Missing Modality in Multimodal Learning),使用貝葉斯元學習來同時實現兩個目標:靈活性(在訓練、測試或兩者中處理缺失模態)和效率(從不完整的模態中高效學習)。核心思想是通過擾動潛在特征空間,使單一模態的嵌入能夠近似全模態的嵌入。為了驗證這一方法的有效性,作者在三個流行的基準數據集(MM-IMDb, CMU-MOSI 和 avMNIST)上進行了一系列實驗。結果表明,SMIL在處理嚴重模態缺失的多模態學習問題方面,相比現有方法和生成型基準(如自編碼器和生成對抗網絡)具有更好的性能。
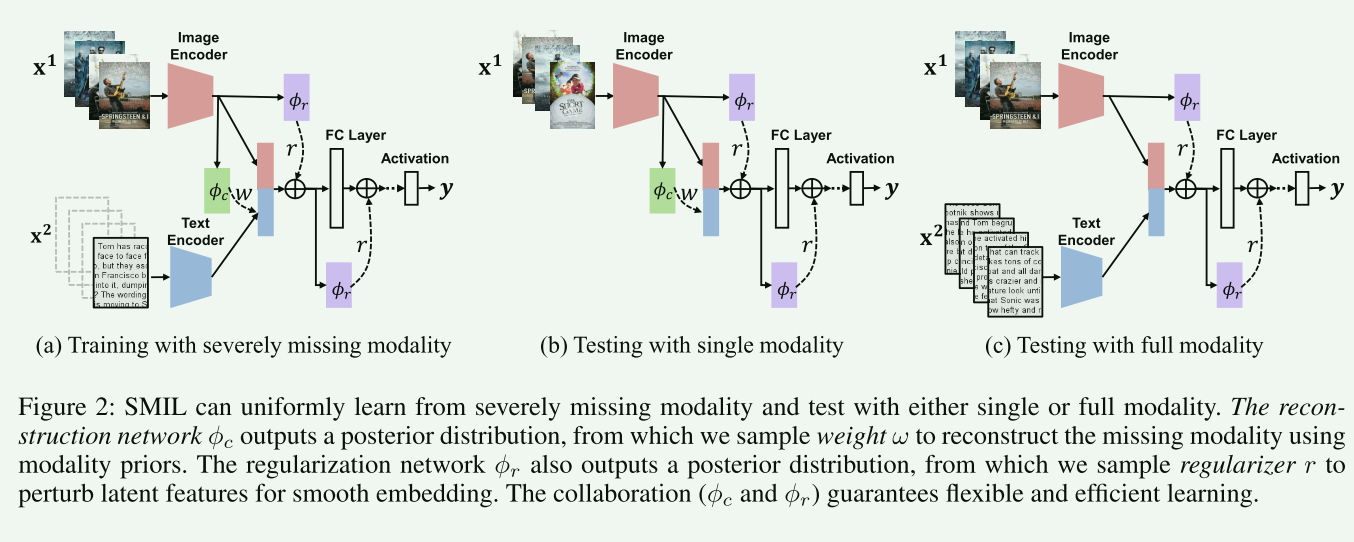
- 模態重建
模態重建是通過使用重建網絡來實現的。該網絡利用可用的模態信息來生成缺失模態的近似值,從而在潛在特征空間中生成完整的數據,并促進兩個方面的靈活性。一方面,該模型可以通過使用完整和不完整的數據進行聯合訓練來挖掘混合數據的全部潛力。另一方面,在測試時,通過打開或關閉特征重建網絡,該模型可以以統一的方式處理不完整或完整的輸入。具體來說,重建網絡被訓練來預測先驗權重的權重,而不是直接生成缺失模態。這是通過學習一組可以使用 K-means 或 PCA 在所有模態完整樣本之間聚類的模態先驗 M 來實現的。然后,通過計算模態先驗的加權和來重建缺失模態。這種方法可以有效地處理缺失模態問題,并在實驗中取得了良好的結果。
- 不確定性引導特征正則化
該網絡通過對特征進行擾動來評估數據的不確定性,并將不確定性評估用作特征正則化,以克服模型和數據偏差。具體來說,該網絡使用一組隨機噪聲向量來擾動輸入特征,并計算每個擾動的輸出的方差。然后,將方差用作特征正則化的權重,以減少特征之間的差異。這種方法可以有效地處理低質量和不完整的特征,并提高多模態模型的魯棒性和泛化能力。與之前的確定性正則化方法相比,不確定性引導特征正則化可以顯著提高模型的容量和性能。
- 貝葉斯元學習框架
通過利用貝葉斯元學習框架來聯合優化所有網絡實現的。具體來說,主網絡 f θ f_{\theta} fθ?在重構 f ? ? f_{\phi_{\phi}} f????網絡和正則化 f ? r f_{\phi_{r}} f?r??網絡的幫助下在 D m D_m Dm?上進行元訓練。然后,在 D f D_f Df?上對更新后的主網絡 f θ ? f_{\theta^{*}} fθ??進行元測試。最后,通過梯度下降元更新網絡參數 { θ , ? c , ? r } \left\{\boldsymbol{\theta}, \boldsymbol{\phi}_{c}, \boldsymbol{\phi}_{r}\right\} {θ,?c?,?r?}。該框架旨在優化目標函數,即最小化 L ( D f ; θ ? , ψ ) \mathcal{L}\left(\mathcal{D}^{f} ; \boldsymbol{\theta}^{*}, \boldsymbol{\psi}\right) L(Df;θ?,ψ),其中 θ ? = θ ? α ? θ L ( D m ; ψ ) \boldsymbol{\theta}^{*}=\boldsymbol{\theta}-\alpha \nabla_{\boldsymbol{\theta}} \mathcal{L}\left(\mathcal{D}^{m} ; \boldsymbol{\psi}\right) θ?=θ?α?θ?L(Dm;ψ), ψ = { ? c , ? r } \psi=\left\{\phi_{c}, \phi_{r}\right\} ψ={?c?,?r?}表示重構和正則化網絡參數的組合。貝葉斯元學習的目標是最大化條件似然: log ? p ( Y ∣ X ; θ ) \log p(\mathbf{Y} \mid \mathbf{X} ; \boldsymbol{\theta}) logp(Y∣X;θ)。然而,解決它涉及到不可行的真后驗 p ( z ∣ X ) p(z|X) p(z∣X)。因此,通過一種分攤分布 q ( z ∣ X ; ψ ) q(z|X;ψ) q(z∣X;ψ)來近似真后驗分布,并且近似的下限形式可以定義為 L θ , ψ = E q ( z ∣ X ; θ , ψ ) [ log ? p ( Y ∣ X , z ; θ ) ] ? KL ? [ q ( z ∣ X ; ψ ) ∥ p ( z ∣ X ) ] . \begin{aligned} \mathcal{L}_{\boldsymbol{\theta}, \boldsymbol{\psi}}=\boldsymbol{E}_{q(\mathbf{z} \mid \mathbf{X} ; \boldsymbol{\theta}, \boldsymbol{\psi})}[\log p(\mathbf{Y} \mid \mathbf{X}, \mathbf{z} ; \boldsymbol{\theta})]- & \operatorname{KL}[q(\mathbf{z} \mid \mathbf{X} ; \boldsymbol{\psi}) \| p(\mathbf{z} \mid \mathbf{X})] . \end{aligned} Lθ,ψ?=Eq(z∣X;θ,ψ)?[logp(Y∣X,z;θ)]??KL[q(z∣X;ψ)∥p(z∣X)].?
我們通過蒙特卡羅(MC)抽樣來最大化這個下界




)










-------監控udp延遲)
?)



