1.遍歷二叉樹
?在二叉樹的一些應用中,常常要求在樹中查找具有某種特征的結點,或者對樹中全部結點逐一進行某種處理。這就引入了遍歷二叉樹的問題,即如何按某條搜索路徑訪問樹中的每一個結點,使得每一個結點僅且僅被訪問一次。 ? ?
遍歷二叉樹:是指按照某種方法順著某一條搜索路徑尋訪二叉樹的結點,使得每個結點均被訪問一次且僅被訪問一次。
1.遞歸遍歷
一棵二叉樹由根結點、根結點的左子樹和根結點的右子樹3部分組成,因而只要依次遍歷這3部分,就能遍歷整棵二叉樹。 ? ?
遍歷的次序:假如以L、D、R分別表示遍歷左子樹、遍歷根結點和遍歷右子樹,遍歷整個二叉樹則有DLR、LDR、LRD、DRL、RDL、RLD六種遍歷方案。若規定先左后右,則只有前三種情況,分別規定為: ? ? ?
DLR——先(根)序遍歷, ? ? ?
LDR——中(根)序遍歷, ? ? ?
LRD——后(根)序遍歷。
1.先序遍歷
先序遍歷二叉樹算法的框架是 :若二叉樹為空,遍歷結束,否則: 訪問根結點; 先序遍歷根結點的左子樹; 先序遍歷根結點的右子樹。

void PreOrder(BiTree bt) /* bt為指向根結點的指針*/
{if (bt) /*如果bt為空,結束*/{visit (bt ); /*訪問根結點*/PreOrder (bt -> lchild); /*先序遍歷左子樹*/PreOrder (bt -> rchild); /*先序遍歷右子樹*/}
}
2.中序遍歷
中序遍歷二叉樹算法的框架是: 若二叉樹為空,遍歷結束,否則: 中序遍歷根結點的左子樹; 訪問根結點; 中序遍歷根結點的右子樹。

void InOrder(BiTree bt)/* bt為指向二叉樹根結點的指針*/
{if (bt ) /*如果bt為空,結束*/{InOrder (bt -> lchild); /*中序遍歷左子樹*/Visit (bt); /*訪問根結點*/InOrder (bt -> rchild); /*中序遍歷右子樹*/}
}
3.后序遍歷
后序遍歷二叉樹算法的框架是:若二叉樹為空,遍歷結束,否則 后序遍歷根結點的左子樹; 后序遍歷根結點的右子樹; 訪問根結點。

void PostOrder(BiTree bt)
/* bt為指向二叉樹根結點的指針*/
{if (bt ) /*如果bt為空,結束*/{PostOrder (bt -> lchild);/*后序遍歷左子樹*/PostOrder (bt -> rchild);/*后序遍歷右子樹*/visit (bt ); /*訪問根結點*/}
}
通過上述三種不同的遍歷方式得到三種不同的線性序列,它們的共同的特點是有且僅有一個開始結點和一個終端結點,其余各結點都有且僅有一個前驅結點和一個后繼結點。 ? ?
從二叉樹的遍歷定義可知,三種遍歷算法的不同之處僅在于訪問根結點和遍歷左右子樹的先后關系。如果在算法中隱去和遞歸無關的語句visit(),則三種遍歷算法是完全相同的。遍歷二叉樹的算法中的基本操作是訪問結點,顯然,不論按那種方式進行遍歷,對含n個結點的二叉樹,其時間復雜度均為O(n)。所含輔助空間為遍歷過程中占的最大容量,即樹的深度。最壞的情況下為n,則空間復雜度也為O(n)。
4.層序遍歷
?二叉樹的層次遍歷:是指從二叉樹的第一層(根結點)開始,從上至下逐層遍歷,在同一層中,按從左到右的順序對結點逐個進行訪問。

利用隊列來實現? ? :
算法思想:遍歷從二叉樹的根結點開始,首先將根結點入隊列,然后執行下面的操作: ?? ? ?
1)取出隊頭元素; ? ? ? ?
2) 訪問該元素所指結點; ? ? ? ?
3) 若該元素所指結點的左、右孩子結點非空,則將該元素所指結點的左孩子指針和右孩子指針入隊。 ? ? ? ?
4)若隊列非空,重復1)-3);當隊列為空時,二叉樹的層次遍歷結束。
void LevelOrder( BiTree bt) /*層次遍歷二叉樹bt算法*/
{ 初始化隊列Q;if ( bt == NULL ) return;bt入隊列Q;while( 隊列Q不空){ p?出隊元素;Visit( p); /*訪問出隊結點*/if ( p->lchild) /*隊首結點左孩子不空,入隊*/{ p->lchild入隊Q }if (p->rchild) /*隊首結點右孩子不空,入隊*/{ p->rchild入隊Q }}
}
5.練習
1.找出分別滿足下面條件的所有二叉樹(非空形態): ? ?
(a)前序序列和中序序列相同; ? ? ?
(b)中序序列和后序序列相同; ? ?
?(c)前序序列和后序序列相同; ? ?
?(d)前序序列、中序序列和后序序列都相同。
2.已知一棵二叉樹的中序序列和后序序列分別為BDCEAFHG和DECBHGFA,畫出這棵二叉樹。

結論:
1) ?由二叉樹的前序序列和中序序列可以唯一確定這棵二叉樹。
2) ?由二叉樹的后序序列和中序序列可以唯一確定這棵二叉樹。
3) ?由二叉樹的前序序列和后序序列不能唯一確定這棵二叉樹。
2.非遞歸遍歷
二叉樹前序遍歷的非遞歸算法的關鍵:在前序遍歷過某結點的整個左子樹后,如何找到該結點的右子樹的根指針。
解決辦法:在訪問完該結點后,將該結點的指針保存在棧中,以便以后能通過它找到該結點的右子樹。

1.先序遍歷
先序算法執行軌跡
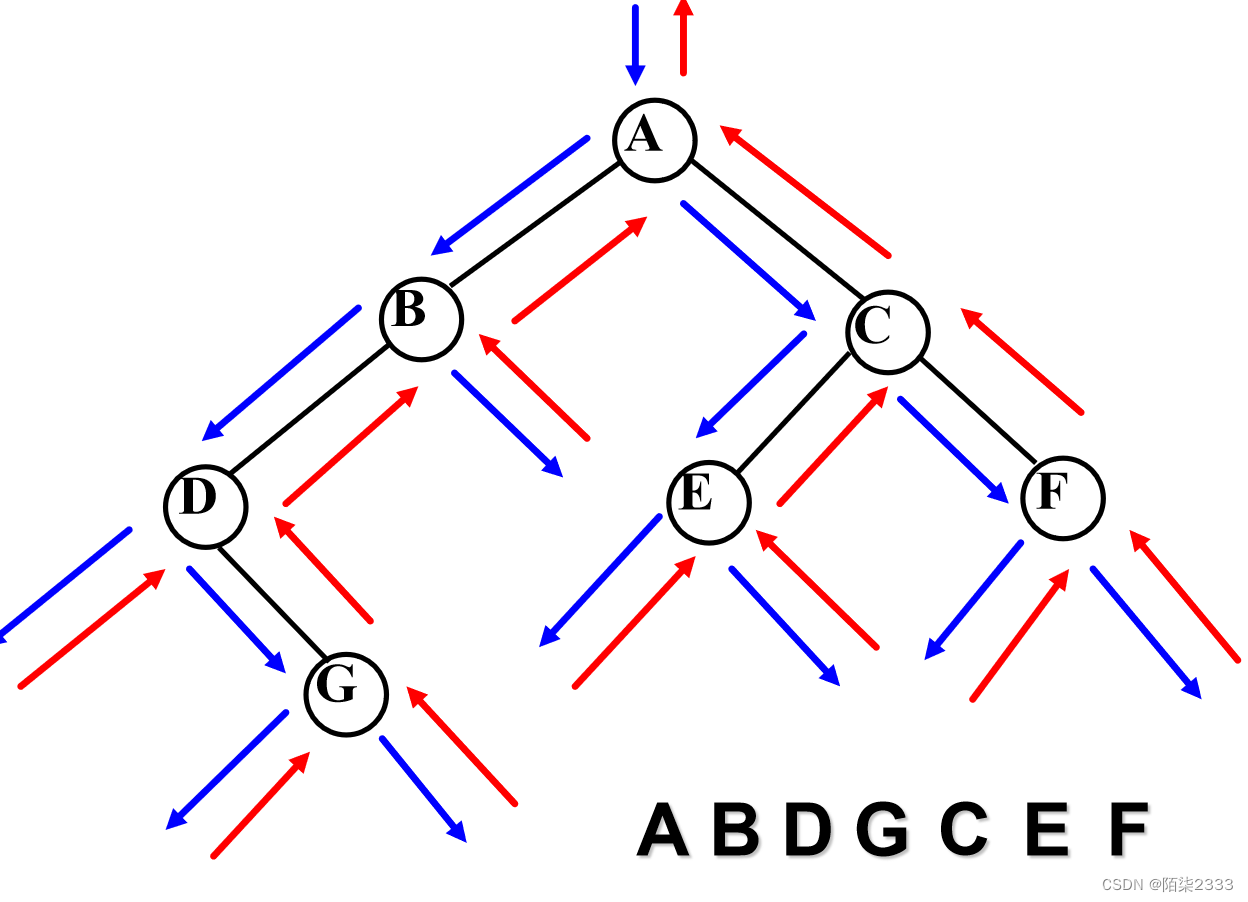
步驟:
1.棧s初始化;
2.循環直到root為空或棧s為空
2.1 當root不空時循環
2.1.1 輸出root->data;(可將輸出變為任何處理) ? ?
2.1.2 將指針root的值保存到棧中; ? ?
2.1.3 繼續遍歷root的左子樹
2.2 如果棧s不空,則
2.2.1 將棧頂元素彈出至root;
2.2.2 準備遍歷root的右子樹;
//先序遍歷
Void Firstorder(BiTree bt)
{ p=bt; /*根結點為當前結點*/
S=Initial( ); /*初始化棧*/
While(p||!Empty(S))
{
While(p) /*當前結點不空*/
{ visit(p); /*訪問結點*/
Push(S,p); /*當前結點入棧*/
p=p->Lchild; /*左孩子作為當前結點*/}
If(!Empty(S)) /*棧不空*/
{
p=pop(s); /*出棧*/
p=p->Rchild; /*右孩子作為當前結點*/
}
}
}
2.中序遍歷
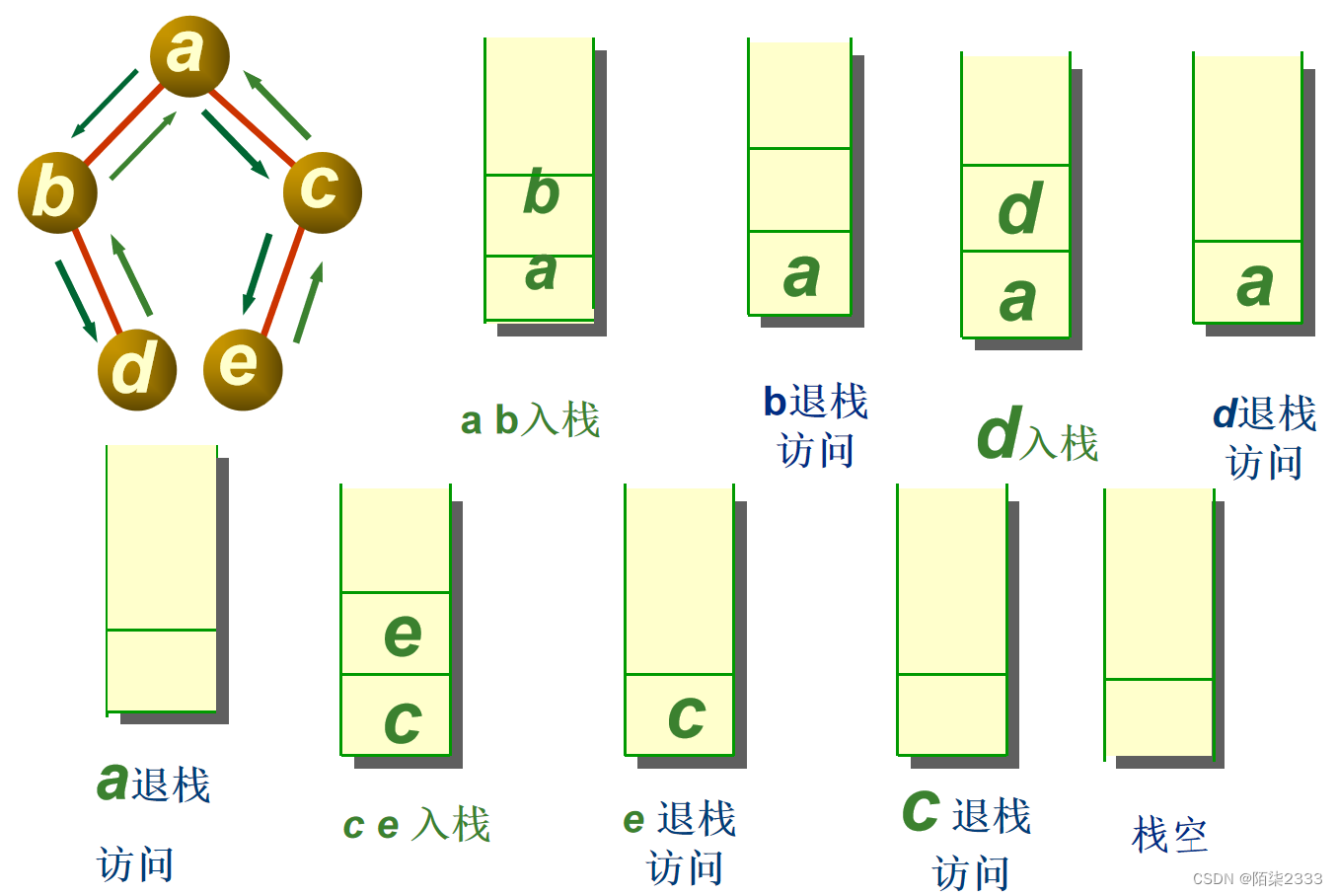
//中序遍歷
Void Inorder(BiTree bt)
{ p=bt; /*根結點為當前結點*/
S=Initial( ); /*初始化棧*/
While(p||!Empty(S))
{
While(p) /*當前結點不空*/
{
Push(S,p); /*當前結點入棧*/
p=p->Lchild; /*左孩子作為當前結點*/}
If(!Empty(S)) /*棧不空*/
{
p=pop(s); /*出棧*/
Visit(p); /*訪問結點*/
p=p-Rchild; /*右孩子作為當前結點*/
}
}
}3.后序遍歷
typedef enum{L,R} tagtype; /*定義枚舉類型*/
typedef struct {
Bitree ptr;
tagtype tag;
}stacknode; /*定義棧結點類型*/
typedef struct{
stacknode Elem[maxsize];
int top;
}SqStack; /*定義順序棧*/void PostOrderUnrec(Bitree bt) /*后序遍歷算法*/{ p=bt;If(!p) return;
do
{ while (p) ?? ??? /*遍歷左子樹*/?? ???
{
x.ptr = p; ? ?? ??
x.tag = L; ?? ?? /*標記為左子樹*/?? ?? ??
push(s,x); /*入棧*/
p=p->lchild; /*左孩子作為當前結點*/
} ?? ???
while (!StackEmpty(s) && s.Elem[s.top].tag==R) { ?? ?
x = pop(s);
p = x.ptr;
visite(p); //tag為R,表示右子樹訪問完畢,故訪問根結點 ?? ?? ?
}if (!StackEmpty(s)){?? ?? ??
s.Elem[s.top].tag =R; ??? /*遍歷右子樹*/?? ?? ??
p=s.Elem[s.top].ptr->rchild; ??/*右孩子作為當前結點*/ ????? ???
}
}while (!StackEmpty(s));
} 4.練習
1.交換二叉樹各結點的左、右子樹(遞歸算法)
void unknown ( BiTree T ){BiTreeNode *p = T, *temp;if ( p != NULL ) {temp = p->lchild; p->lchild = p->rchild;p->rchild = temp;unknown ( p->lchild );unknown ( p->rchild );}}
2.不用棧消去遞歸算法中的第二個遞歸語句 (即消去尾遞歸)
void unknown ( BiTree T )
{BiTreeNode *p = T, *temp;while ( p != NULL ) {temp = p->lchild; p->lchild = p->rchild;p->rchild = temp;unknown ( p->lchild );p = p->rchild;}}3.使用棧消去遞歸算法中的兩個遞歸語句
void unknown ( BiTree T )
{BiTreeNode *p, *temp,S[Max]; int top=-1; if ( T != NULL )
{top++;S[top]= T;while ( top>-1 ){p=S[top]; top--; /*棧中退出一個結點*/temp = p->lchild; /*交換子女*/p->lchild = p->rchild;p->rchild = temp;if ( p->rchild != NULL )top++;S[top]= p->rchild;if ( p->lchild != NULL )top++;S[top]= p->p->lchild;}}
}
2.應用
1.設計算法輸出二叉樹的所有葉子結點的值。
基本思想: ? ? ? ?
若二叉樹為空樹,則葉子數目為0。 ? ? ? ?
對于一棵非空二叉樹,如果它的左子樹和右子樹都為空,那么此二叉樹只有一個結點,就是葉子,此時葉子數目為1;否則,二叉樹的葉子數目為左子樹葉子數目和右子樹葉子數目的總和。
int BitreeLeaf ( BiTree bt )
{if ( bt == NULL ) return 0 ; /* 空樹,葉子數為0 */if ( bt->lchild ==NULL&& bt->rchild == NULL) return 1 ; /*只有一個根結點,葉子數為1*/return ( BitreeLeaf ( bt -> lchild ) + BitreeLeaf ( bt -> rchild )) ;
}
2.設計算法求二叉樹的深度。
基本思想: ? ? ?
若二叉樹為空,約定二叉樹的深度為0; ? ? ?
對于一棵二叉樹,如果它的左子樹和右子樹都為空,那么此二叉樹只有一個根結點,此時二叉樹的深度為1;否則,先求出其左、右子樹的深度depthL和depthR,那么整棵二叉樹的深度為1+max(depthL,depthR)。
int BitreeDepth ( BiTree bt )
{ int d = 0,depthL, depthR; /*depthL和depthR分別為左、右子樹的深度*/if ( bt == NULL ) return 0 ; /*空樹,深度為0 */if ( bt -> lchild ==NULL && bt -> rchild == NULL) return 1; /*葉子結點,深度為1 */depthL = BitreeDepth ( bt -> lchild ) ; /*左子樹深度 */depthR = BitreeDepth ( bt -> rchild ) ; /*右子樹深度 */d = max (depthL , depthR ) /*d為左右子樹中較深者的深度*/return d+1 ; /* 整棵二叉樹的深度為左、右子樹中較深者的深度+1 */
}
3.創建二叉樹
創建二叉樹的方法有兩種,一種是給定一棵二叉樹的先序遍歷序列和中序遍歷序列創建二叉樹,另一種是給定一棵二叉樹的“擴展先序遍歷序列”創建二叉樹。
(1)結合先序遍歷序列和中序遍歷序列創建二叉樹 ? ? ? ? ? ?
基本思想:
先序遍歷的第一個結點一定是二叉樹的根結點,而根據中序遍歷規則,這個結點將同一棵二叉樹的中序遍歷序列分成了左、右兩部分,左邊部分是二叉樹的根結點的左子樹的中序遍歷序列,右邊部分是二叉樹的根結點的右子樹的中序遍歷序列。根據這兩個子序列,在先序序列中找到對應的子序列,左子序列的第一個結點為左子樹的根結點,右子序列的第一個結點為右子樹的根結點。對左右子樹,再反復利用這個方法,最終根據先序序列和中序序列能唯一地確定出一棵二叉樹。
(2)結合“擴展先序遍歷序列”創建二叉樹。 ? ?
擴展先序遍歷序列:
就是先對原有二叉樹用空子樹進行擴展,使每個結點的左右子樹(包括空子樹)都存在,然后再對擴展后的二叉樹進行先序遍歷。遍歷序列中用特定的符號表示空子樹。
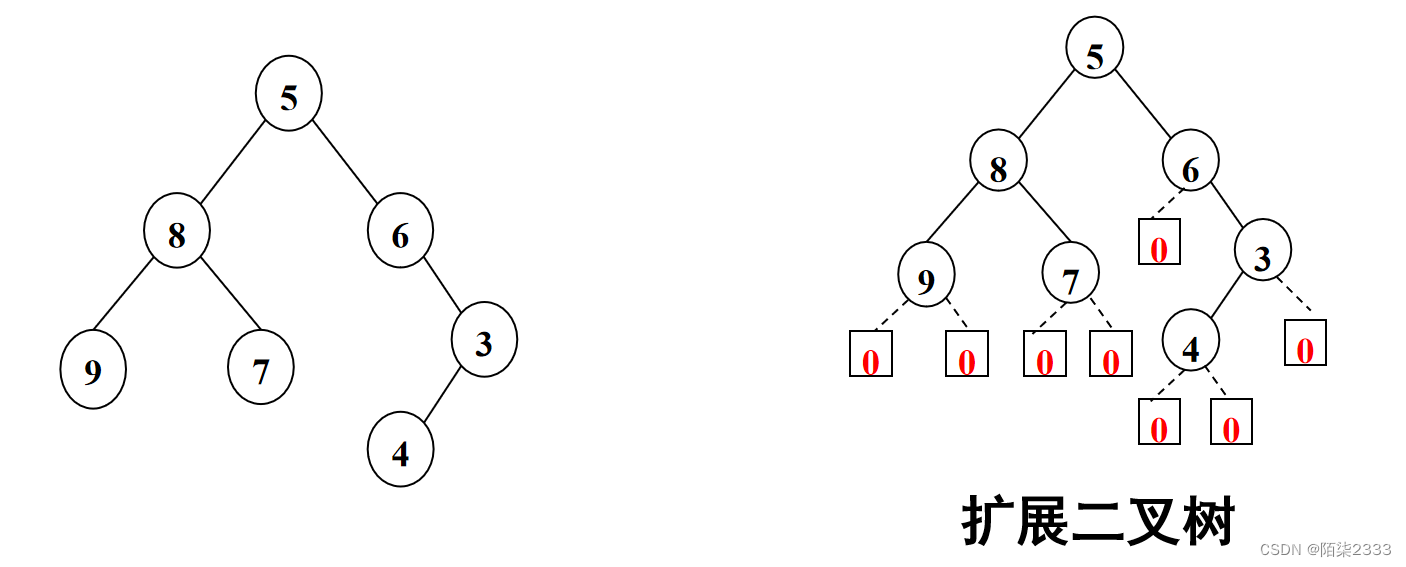
其擴展先序遍歷序列為:
5 8 9 0 0 7 0 0 6 0 3 4 0 0 0 ? ?
其中“0”表示空子樹。
BiTree CreateBiTree(char str[])
{ BiTree bt;static int i=0;char c = str[i++];if( c==‘.’ ) bt = NULL;/* 創建空樹 */else{ bt = (BiTree)malloc(sizeof(BiTreeNode)); bt->data = c; /* 創建根結點 */bt->lchild = CreateBiTree(str); /* 創建左子樹 */bt->rchild = CreateBiTree(str); /* 創建右子樹 */}return bt;
}





)













