1? K-means介紹
1.0 方法介紹
- KMeans算法通過嘗試將樣本分成n個方差相等的組來聚類,該算法要求指定群集的數量。它適用于大量樣本,并已在許多不同領域的廣泛應用領域中使用。
- KMeans算法將一組樣本分成不相交的簇,每個簇由簇中樣本的平均值描述。這些平均值通常稱為簇的“質心”;
- 注意,質心通常不是樣本點,盡管它們存在于相同的空間中。
- KMeans算法旨在選擇最小化慣性或稱為群內平方和標準的質心:
1.1 慣性的缺點
- 慣性可以被認為是衡量簇內部一致性的一種度量。它有各種缺點:
- 慣性假設簇是凸形的和各向同性的,但這不總是情況。
- 它對于拉長的簇或形狀不規則的流形反應不佳。
- 慣性不是一個規范化的度量:
- 我們只知道較低的值更好,零是最優的。但是在非常高維的空間中,歐幾里得距離往往會變得膨脹(這是所謂的“維數詛咒”的一個實例)。
- ——>在k均值聚類之前運行一個降維算法,如主成分分析(PCA),可以緩解這個問題并加快計算速度。
- 慣性假設簇是凸形的和各向同性的,但這不總是情況。
- 以下是幾個K-means效果不加的例子:

- clusters的數量不是最優
- 各向異性的cluster分布
- 方差不同
- 各個簇數量不同
1.2 Kmeans算法的步驟
- K均值算法通常被稱為勞埃德算法(Lloyd's algorithm)。簡單來說,該算法有三個步驟
- 第一步選擇初始質心,最基本的方法是從數據集中選擇樣本
- 初始化之后,K均值算法由兩個步驟的循環組成
- 第一個步驟是將每個樣本分配給最近的質心
- 第二步是通過取分配給每個前一個質心的所有樣本的平均值來創建新的質心
- 計算舊質心和新質心之間的差異,并重復這最后兩個步驟,直到這個值小于一個閾值(直到質心不再有顯著移動為止)
- K均值算法等同于期望最大化算法,帶有一個小的、全相等的、對角線協方差矩陣

- 給定足夠的時間,K均值總會收斂,但這可能是到一個局部最小值
- 這在很大程度上取決于質心的初始化
- 因此,計算通常會進行多次,質心的初始化也各不相同
- 一個幫助解決這個問題的方法是k-means++初始化方案(init='k-means++')
- 這樣初始化質心通常會相互遠離,導致比隨機初始化更好的結果
2 sklearn.cluster.KMeans
sklearn.cluster.KMeans(n_clusters=8, *, init='k-means++', n_init='warn', max_iter=300, tol=0.0001, verbose=0, random_state=None, copy_x=True, algorithm='lloyd')2.1 主要參數
| n_clusters | 簇的數量 |
| init |
|
| n_init |
|
| max_iter |
|
| tol | 兩次連續迭代的簇中心的Frobenius范數差異來聲明收斂的相對容忍度 |
2.2 舉例
from sklearn.cluster import KMeans
import numpy as npX = np.array([[1, 2], [1, 4], [1, 0],[10, 2], [10, 4], [10, 0]])kmeans=KMeans(n_clusters=2,n_init='auto').fit(X)2.2.1 屬性
| cluster_centers_ | 簇中心的坐標
|
| labels_ | 每個點的標簽
|
| inertia_ | 樣本到最近簇中心的平方距離之和,如果提供了樣本權重,則按樣本權重加權
|
| n_iter_ | 運行的迭代次數
|
2.2.2 fit
fit(X, sample_weight=None)?sample_weight 是X中每個觀測的權重。如果為None,則所有觀測都被賦予相等的權重
3?sklearn.cluster.kmeans_plusplus
類似于使用k_means++來進行
sklearn.cluster.kmeans_plusplus(X, n_clusters, *, sample_weight=None, x_squared_norms=None, random_state=None, n_local_trials=None)| X | 用來選擇初始種子的數據 (也就是KMeans里面fit的內容) |
| n_cluster | 要初始化的質心數量 |
| sample_weight | X中每個觀測的權重 |
3.1 返回值:
centers:形狀為(n_clusters, n_features) ,k-means的初始中心。
indices:形狀為(n_clusters,) 在數據數組X中選擇的中心的索引位置。對于給定的索引和中心,X[index] = center
3.2 舉例
from sklearn.cluster import kmeans_plusplus
import numpy as npX = np.array([[1, 2], [1, 4], [1, 0],[10, 2], [10, 4], [10, 0]])kmeans_plusplus(X,n_clusters=2)
'''
(array([[10, 0],[ 1, 4]]),array([5, 1]))
'''4?Mini Batch K-Means
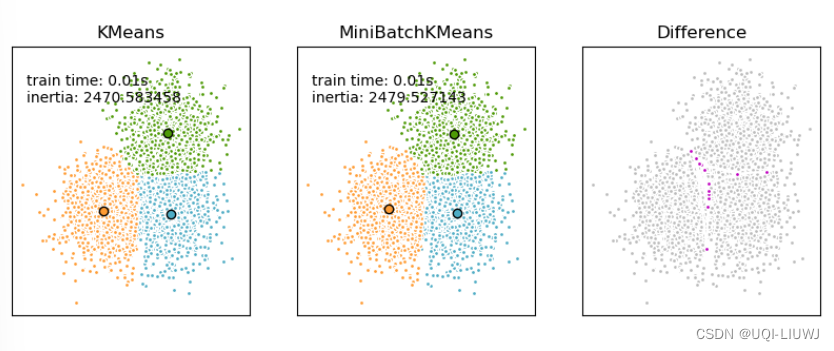
- MiniBatchKMeans是KMeans算法的一個變種,它使用小批量(mini-batches)來減少計算時間,同時仍然試圖優化相同的目標函數
- 小批量是輸入數據的子集,在每次訓練迭代中隨機采樣
- 這些小批量大大減少了收斂到局部解所需的計算量
- 與其他減少k-means收斂時間的算法不同,mini-batch k-means產生的結果通常只比標準算法稍差
- 該算法在兩個主要步驟之間迭代,類似于傳統的k-means算法
- 在第一步中,從數據集中隨機抽取樣本,形成一個小批量.然后,這些樣本被分配到最近的質心
- 在第二步中,更新質心。與k-means不同,這是按樣本進行的
- 對于小批量中的每個樣本,通過取樣本及其之前分配到該質心的所有樣本的流式平均值來更新分配的質心。
- 這樣做的效果是隨著時間的推移減少質心變化的速率。
- 這些步驟執行直到收斂或達到預定的迭代次數為止
- MiniBatchKMeans比KMeans收斂得更快,但結果的質量有所降低
4.1?sklearn.cluster.MiniBatchKMeans
class sklearn.cluster.MiniBatchKMeans(n_clusters=8, *, init='k-means++', max_iter=100, batch_size=1024, verbose=0, compute_labels=True, random_state=None, tol=0.0, max_no_improvement=10, init_size=None, n_init='warn', reassignment_ratio=0.01)4.1.1 主要參數
| n_clusters | 簇的數量 |
| init |
|
| max_iter |
|
| batch_size | mini batch的大小,默認是1024 |
| n_init |
|
?4.1.2 屬性
還是那些:cluster_centers,labels_,inertia_,n_iter_,n_steps
4.1.3 方法
方法上fit,tranform,predict這些都有,多了一個partial_fit,表示使用一個mini-batch的樣本
4.2 舉例
from sklearn.cluster import MiniBatchKMeans
import numpy as npX = np.array([[1, 2], [1, 4], [1, 0],[10, 2], [10, 4], [10, 0]])mini_kmeans=MiniBatchKMeans(n_clusters=2).fit(X)mini_kmeans.cluster_centers_
'''
array([[ 1. , 2.57142857],[10. , 2. ]])
'''mini_kmeans.labels_
#array([0, 0, 0, 1, 1, 1])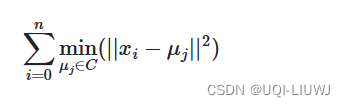









![ElementPlusError: [ElOnlyChild] no valid child node found](http://pic.xiahunao.cn/ElementPlusError: [ElOnlyChild] no valid child node found)









 畫中畫)

