40.組合總和II

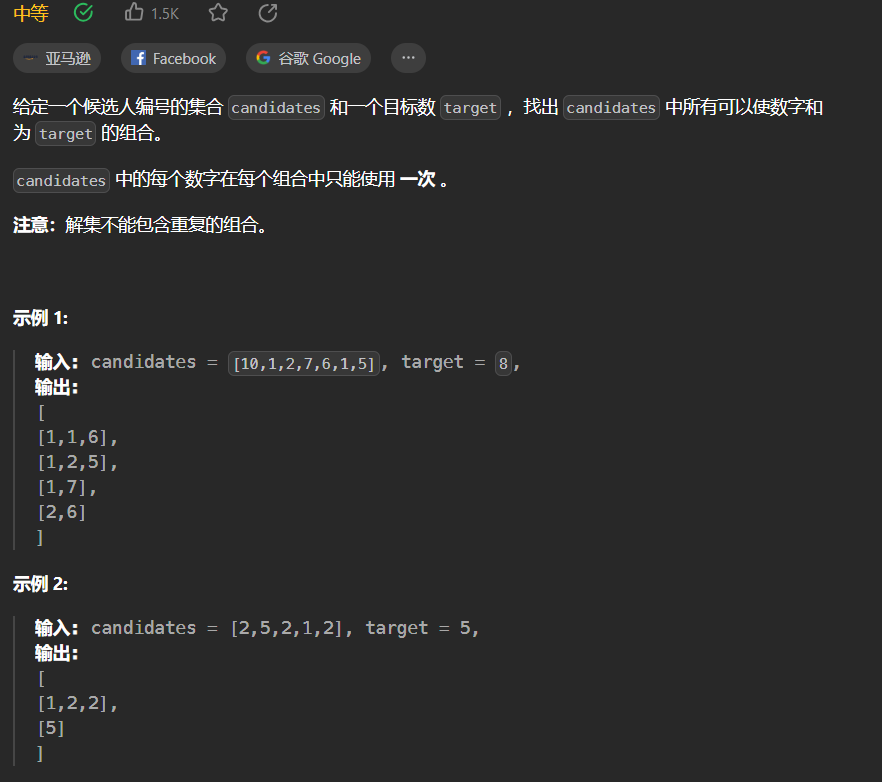
本題詳解：回溯算法

class Solution {public List<List<Integer>> combinationSum2(int[] candidates, int target) {int len = candidates.length;List<List<Integer>> res = new ArrayList<>();if (len == 0) {return res;}// 關鍵步驟Arrays.sort(candidates);Deque<Integer> path = new ArrayDeque<>(len);dfs(candidates, len, 0, target, path, res);return res;}/*** @param candidates 候選數組* @param len        冗余變量* @param begin      從候選數組的 begin 位置開始搜索* @param target     表示剩余，這個值一開始等于 target，基于題目中說明的"所有數字（包括目標數）都是正整數"這個條件* @param path       從根結點到葉子結點的路徑* @param res*/private void dfs(int[] candidates, int len, int begin, int target, Deque<Integer> path, List<List<Integer>> res) {if (target == 0) {res.add(new ArrayList<>(path));return;}for (int i = begin; i < len; i++) {// 大剪枝：減去 candidates[i] 小于 0，減去后面的 candidates[i + 1]、candidates[i + 2] 肯定也小于 0，因此用 breakif (target - candidates[i] < 0) {break;}// 小剪枝：同一層相同數值的結點，從第 2 個開始，候選數更少，結果一定發生重復，因此跳過，用 continueif (i > begin && candidates[i] == candidates[i - 1]) {continue;}path.addLast(candidates[i]);// 因為元素不可以重復使用，這里遞歸傳遞下去的是 i + 1 而不是 idfs(candidates, len, i + 1, target - candidates[i], path, res);path.removeLast();}}
}