在進行數學建模競賽時，很多同學面臨的第一個挑戰是如何對賽題進行歸類，并選擇合適的模型。本篇梳理了數學建模中最常見的幾類賽題，并針對每類題型提供了基本的解決思路，幫助大家快速選擇合適的解題方法，高效完成模型構建。

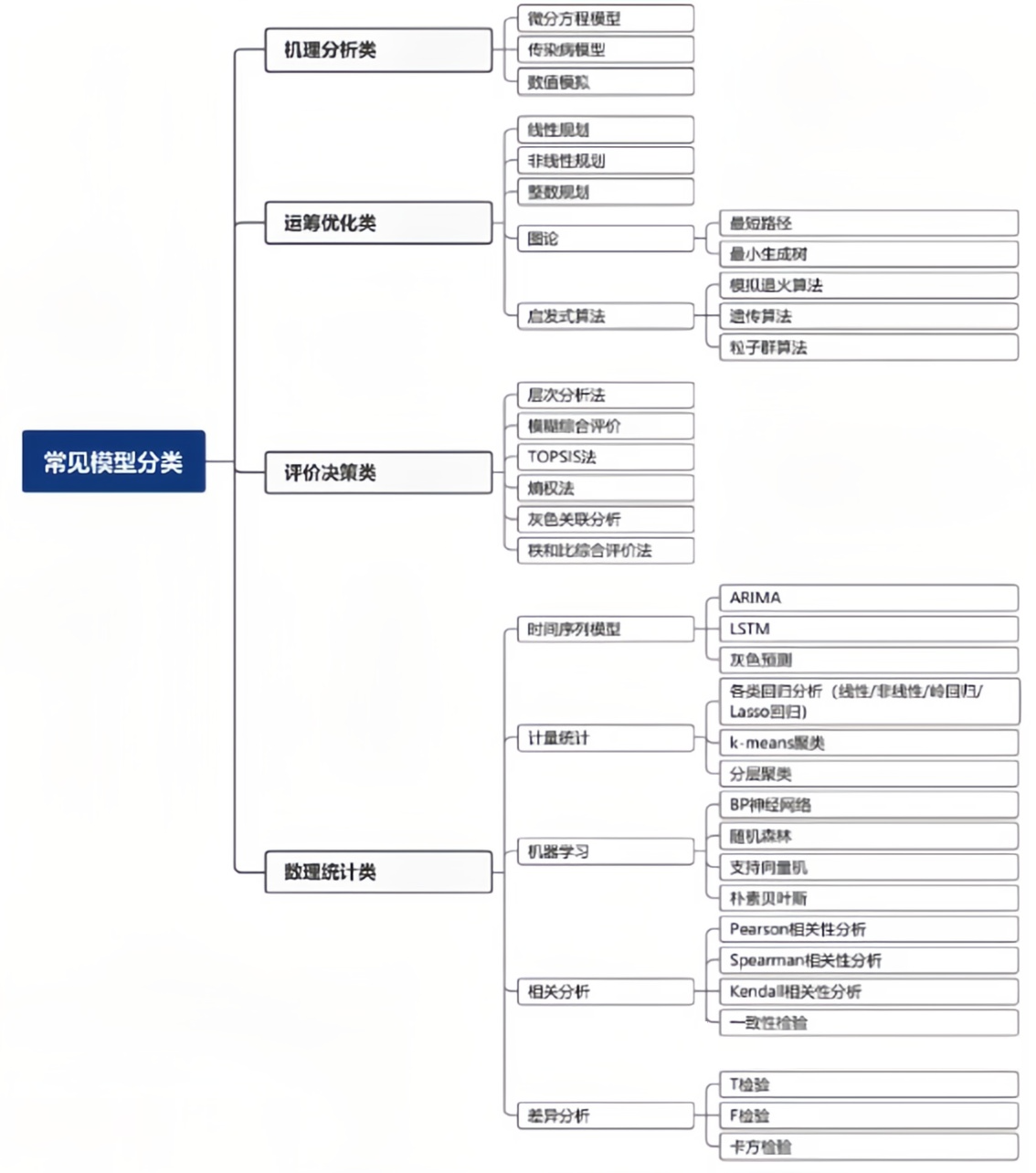
數學建模賽題類型主要分為評價類、預測類和優化類三種，其中優化類是最常見的賽題類型，幾乎每年的地區賽或國賽美賽等均有出題，必須要掌握并且熟悉。機理分析類基本上建立完機理方程后仍然要轉換成優化問題，數理統計類大部分都是和預測相關。

一、評價類問題

1.賽題特征與基本解題步驟

綜合評價是數學建模中的一類常見的問題，在國賽和美賽中都經常出現，例如國賽05年長江水質的綜合評價、2010年上海世博會影響力的定量評估問題、2014年美賽“最好大學教練”問題、2015年的“互聯網+”時代的出租車資源配等，都屬于綜合評價類問題。綜合評價問題是數學建模問題中思路相對清晰的一類題目，從每學期的綜合測評、旅游景點的選擇到挑選手機，評價類問題在生活中也是處處存在。

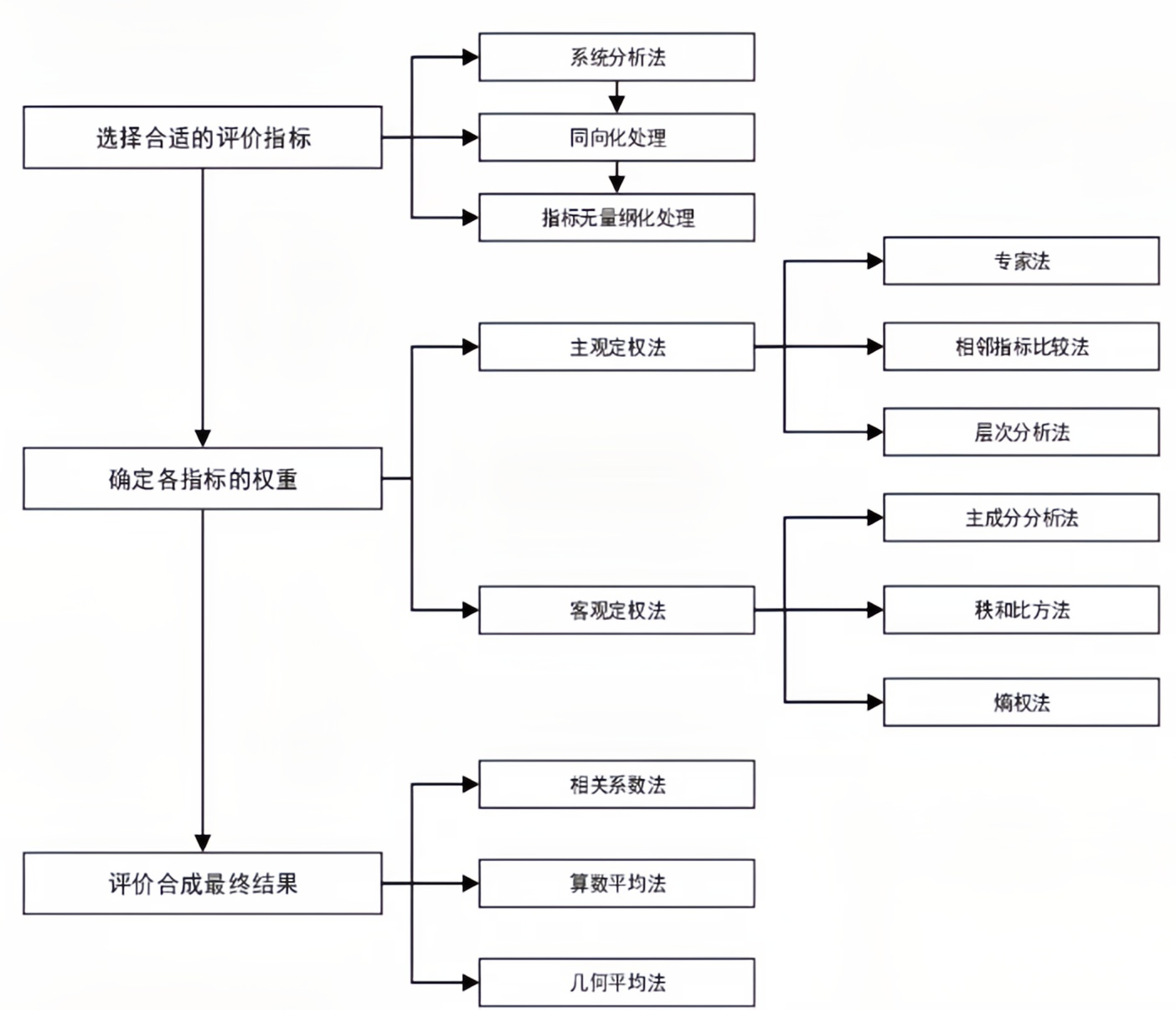
• 評價類問題一般的解題步驟為：選擇合適的評價指標→確定各指標權重→評價合成最終結果

2.主客觀評價問題的區別

主客觀概念主要是在指標定權時來劃分的。

• 主觀評價：在定權時主要以判斷者的主觀經驗為依據
• 客觀評價：主要基于測量數據的基本特性來綜合定權

定權帶有一定的主觀性，用不同方法確定的權重分配，可能不盡一致，這將導致權重分配的不確定性，最終可能導致評價結果的不確定性。因而在實際工作中，不論用哪種方法確定權重分配，都應當依賴于較為合理的專業解釋。

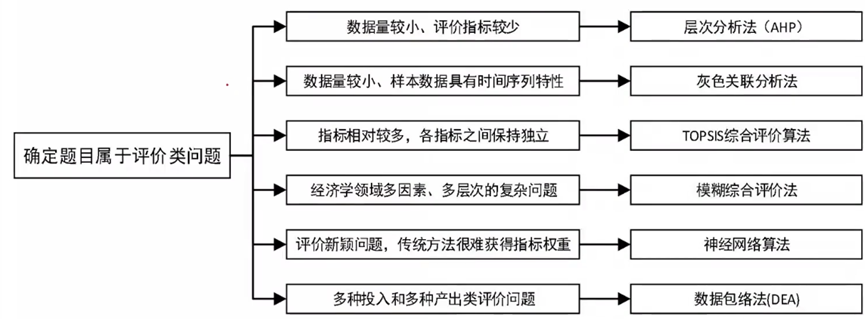
3.如何選擇合適的評價方法

在評價類問題的分析中，如何選擇合適的評價方法是決定評價結果好壞的關鍵因素，因此需要洞悉各常用評價方法的基本特性和使用條件才能順利答題。

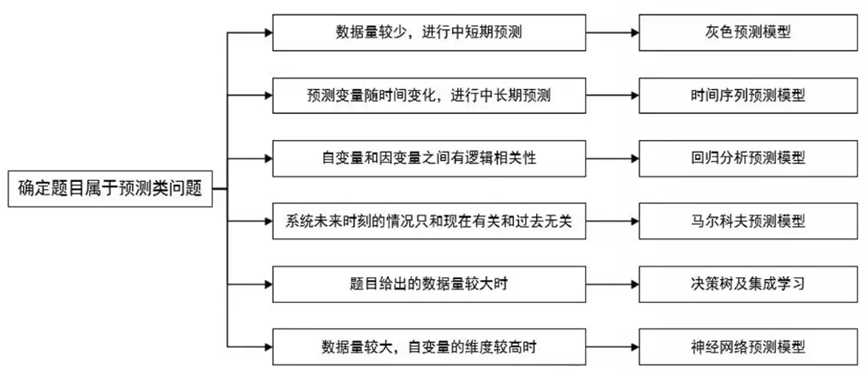
二、預測類問題

1.賽題特征與基本解題步驟

預測就是根據過去和現在估計未來，預測未來。統計預測屬于預測方法研究范疇，即如何利用科學的統計方法對事物的未來發展進行定量推測。基于數學建模的預測方法種類繁多，從經典的單耗法、彈性系數法、統計分析法，到目前的灰色預測法、機器學習等。當在使用相應的預測方法建立預測模型時，我們需要知道主要的一些預測方法的研究特點，優缺點和適用范圍。

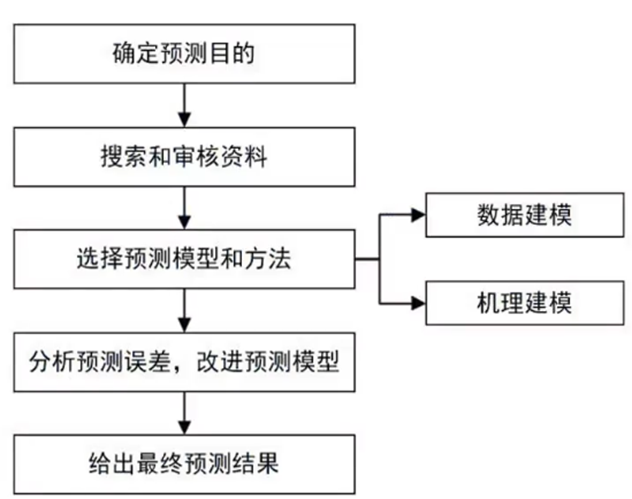
• 預測類問題一般的解題步驟為：確定預測目的→搜索和審核資料→選擇預測模型和方法→分析預測誤差改進模型→給出預測結果

2.預測類問題分類

一類是無法用數學語言刻畫其內部演化機理的問題；另一類是可以通過微分方程刻畫其內部規律，稱為機理建模問題，通過微分方程建模求解。

3.如何選擇合適的預測方法

在預測類問題的分析中，同樣受到預測條件的限制（如數據量的大小、變量之間的關系等），不同的預測方法可能會產生不同的結果，因此需要根據實際情況來選擇。

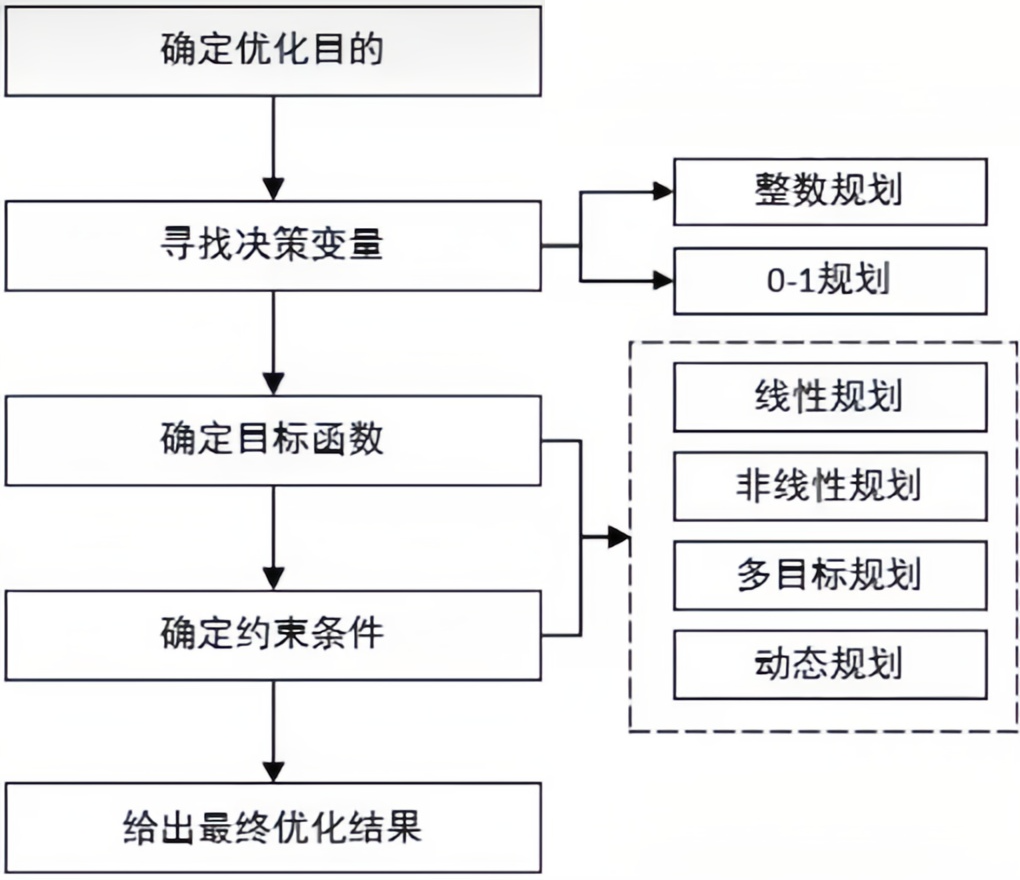
三、優化類問題

1.賽題特征與基本解題步驟

優化類問題是從所有可能方案中選擇最合理的方案以達到最優目標。在各種科學問題、工程問題、生產管理、社會經濟問題中，人們總是希望在有限的資源條件下，用盡可能小的代價，獲得最大的收獲（比如保險）。

優化類問題一般的解題步驟為：

• 確定決策變量，即需要優化的變量；
• 確定目標函數，即優化的目的；
• 確定約束條件，即決策變量在達到最優狀態時，受到哪些客觀限制。

2.部分優化類賽題的解決方案

例1：在08年國賽眼科病床的合理安排問題中——

• 目標函數：醫院病床的利用率最高；
• 決策變量：服務策略，即是先到病人先住院、急診病人先住院還是占用病床時間短的病人先住院等；
• 約束條件：可能包括病人最長等待時間限制、不同癥狀之間的病人不同房等。

例2：在10年國賽交巡警服務平臺的設置與調度問題中——

• 決策變量：服務平臺的位置坐標；
• 目標函數：交巡警車到達事發地時間最短、交巡警封鎖交通要道時間最短；
• 約束條件：可能包括事故發生后交警最晚到達時間，一定區域內服務平臺最低數量要求等。

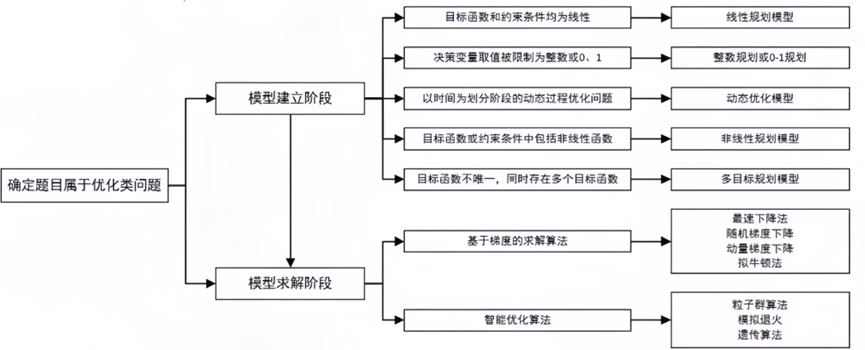
3.如何選擇合適的優化方法

優化類問題中常用的數學模型和求解算法，包括線性規劃、非線性規劃、整數規劃、多目標規劃等。在模型求解中，對于凸優化模型，可以采用基于梯度的求解算法；對于非凸的優化模型，可以采用智能優化算法。